MIT 18.06 linear algebra 第三十一讲笔记
第三十课课程要点:
- Linear Transformations
- Without coordinates: NO Matrix
- With Coordinates Matrix
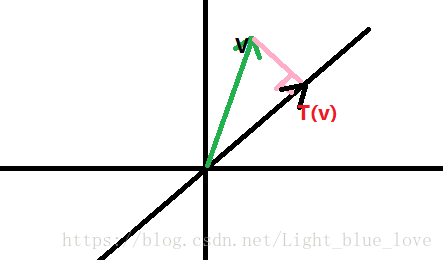
例子一个二维平面中的投影:使得平面中的一个向量变为平面内的另一个向量
满足以下条件的就是线性变换:
-
,其中
为变换的函数,
是向量,
是一个常数。
由上面两条可以推出 。
例子2, ,根据这个式子 。如果给一个向量乘以-2,那么向量的长度肯定不会是乘以-2倍,可以验证出这个变换函数其实并不满足线性变换的要求。
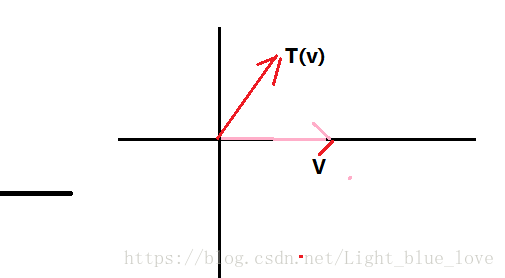
例子3:旋转
这里对向量
进行了逆时针旋转45度。验证一下就可以知道这是一个线性变换,那么如果我们把一群这样的向量做线性变换以后会怎样?
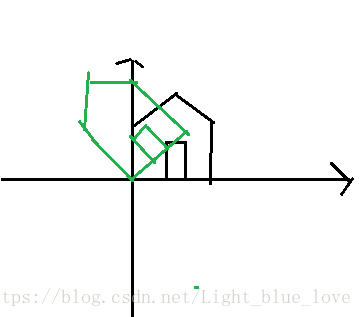
可以看到小房子,被整体旋转了45度。
虽然前面的例子都是画在坐标系中的,但是我们并没有明确指定坐标。在擦掉坐标系,前面的线性变换依旧不受影响。只是为了好看,在前面采放在坐标系中。
现在开始引入坐标,一旦引入坐标,那么线性变换必不可少需要矩阵来帮助表示线性变换的过程。
我们把线性变换写成矩阵与向量乘积的形式:
,可以验证
且
,这样表示满足线性变换的要求。
如果选中一个矩阵
乘以平面中的所有向量,那么就能将整个平面改变。
假设有一个矩阵
,对下面图形中的所有向量做变换:
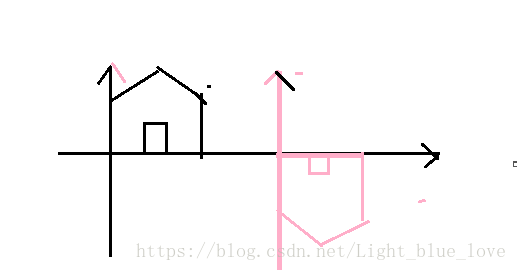
从上图中可以看到变换的效果。
理解线性变换其实就是确定它背后的矩阵。
如果先要了解线性变化对输入向量的硬性就要知道线性变换对基向量的影响。因为空间中的任意向量都是可以用这组基向量来表示 。那么 。
坐标来源于一组基,如果 ,那么这个向量的坐标就是 。
对于线性变换来说,重要的就是来构建出能够表示线性变换 的矩阵 。
对于线性变换 :
- 根据输入空间的一组基来确定输入向量
- 根据输出空间的一组基来确定输出向量
对于输入空间
选择一组基
,对于输出空间
选择一组基
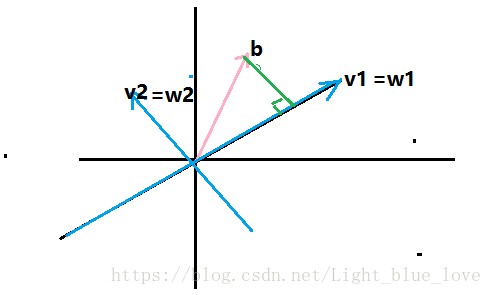
在上图中
,那么这个投影矩阵即为
。
如果是投影在45度直线上,并且都用标准基底 , .那么我们可以用前面学过的方法 来求解投影矩阵。
找到线性变换关系矩阵
的方法:
给定两组基底
和
.
- 首先求矩阵 的第一列,通过 。
- 求矩阵 的第二列,通过
- …..以此类推
那么当我们输入一个向量 时, ,就能告诉我们它在 下的坐标。
求导其实也是一种线性变换:
,当我们输入
,输出为
。
矩阵乘法的本质就是线性变换。