MIT_Linear_Algebra_lec17: 正交基、正交矩阵和施密特正交化

Lecture 17: Orthogonal Matrices and Gram-Schmidt

MIT 公开课：Gilbert Strang《线性代数》课程笔记（汇总

---

标准正交基

$q_i^Tq_j = \left\{\begin{array}{cc} 1 (i = j) \\ 0(i ≠ j) \\ \end{array}\right.$

正交矩阵

定义

Q是正交矩阵，当它的各个列向量都相互正交的时候。

$Q = [q_1 q_2 q_3 ....]$ ( $q_i 是列向量$)

性质

如果Q是正交矩阵，那么

$Q^TQ = \left[ \begin{matrix} \ q_1^T\\ \ q_2^T\\ \ .... \end{matrix} \right] \left[ \begin{matrix} \ q_1 & q_2 & .... \end{matrix} \right] = I$（单位矩阵）
如果Q还是方的，那么Q存在可逆矩阵，并且
$Q^T = Q^-1$

正交矩阵的投影矩阵

P是投影到正交矩阵Q的列空间所对应的投影矩阵。

• 据前几讲，

  $P = Q(Q^TQ)^-1Q^T = QQ^T$

  如果Q是方阵，那么 $P = I$

• 据前几讲， P 满足 $P = P^T$, $P^2 = P$ 在这里同样成立

施密特正交化

过程

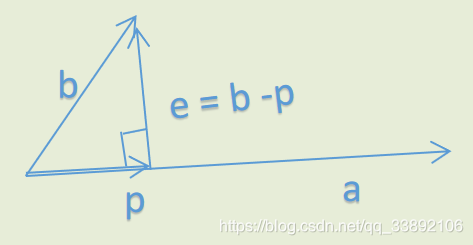
如上图，a和b是两个不相互正交的分量。

施密特正交化就是a不动，找到b中与a正交的分量。

• 方法：
  将b投影到a上，b - 投影分量 = e 就是所要求的。

• 据前几讲， $e = b - (A^Tb/A^TA)A$, 若要归一化再除以长度

一个例子：

A 经过施密特正交化变成Q，但是列空间并没有变