MIT 18.06 linear algebra 第三十四讲笔记

MIT 18.06 linear algebra 第三十四讲笔记

---

第三十四课课程要点：

• 4 subspaces
• left-inverse
• right-inverse
• pseudo-inverse

---

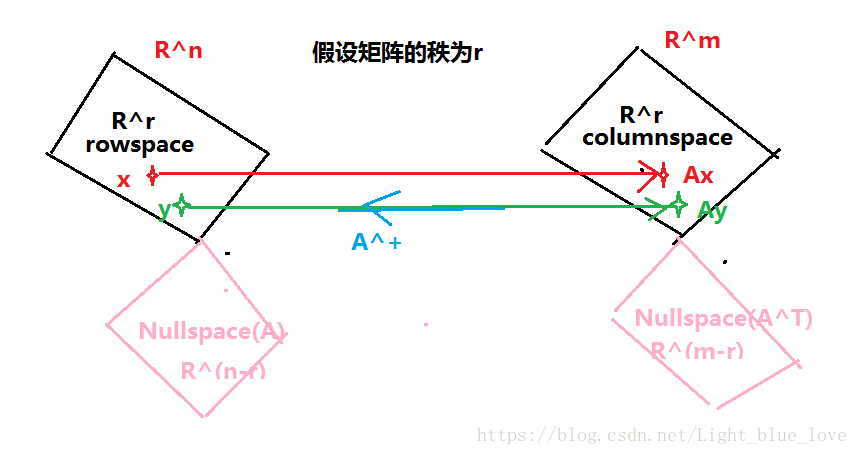
这张图是最前面学到的关于矩阵四个子空间。

有$m\times n$的矩阵$A$,如果矩阵$A$的左右逆都存在即$A^{-1}A=I=AA^{-1}$,那么这个矩阵满足$r=m=n$，即为满秩方阵。

---

左逆-列满秩

如果矩阵$A$是列满秩，即$r=n<m$，矩阵各个列向量是线性独立的，那么矩阵的$N(A)=\{0 \}$。这时矩阵只存在左逆。对于$Ax=b$那么它的解只有一个或者无解。因为如果$b$在矩阵$A$的列空间中的话（即$b$在$N(A)$中），那么既可以得到一个唯一解，如果向量$b$不在矩阵$A$的列空间中，则无解。

如果矩阵$A$的各个列是线性无关的，不论矩阵的形状如何。$A^TA$都是对称且可逆的矩阵。

$\color{red}{(A^TA)^{-1}A^T}A=I_{n\times n}$,左侧红色的部分就被称为矩阵$A$的左逆，即$A_{left}^{-1}=(A^TA)^{-1}A^T$。看到$(A^TA)^{-1}A^T$,是不是似曾相识，它就是前面学到的投影矩阵，这个是在列空间上的投影。

---

右逆-行满秩

假设矩阵$A$为行满秩矩阵，即$r=m<n$且$N(A^T)=\{ 0\}$。在求解$Ax=b$时，由于$A$是行满秩，所以说在消元的时候不会出现全零的行，不会导致消到最后出现$0=b_i$的情形。$x$有$n-m$个自由变量，即$Ax=b$有无穷多个解。由于矩阵$A$是行满秩的，那么$AA^T$是可逆的。

$A\color{red}{A^T(AA^T)^{-1}}=I$,红色的部分就是矩阵$A$的右逆。即$A_{right}^{-1}=A^T(AA^T)^{-1}$。$A^T(AA^T)^{-1}$也是一个投影矩阵，它是在行空间上的投影矩阵。

---

1. 当矩阵$A$两边都存在逆时，两个零空间即$N(A)\quad N(A^T)$均为0向量。
2. 当矩阵$A$只存在左逆时，$N(A)=\{0\}$。
3. 当矩阵$A$只存在右逆时，$N(A^T)=\{0\}$。
4. 当矩阵$A$左右逆均不存在时，$N(A)\quad N(A^T)$都是存在的，不只有零向量。这是$r<n\quad and\quad r<m$。

---

伪逆

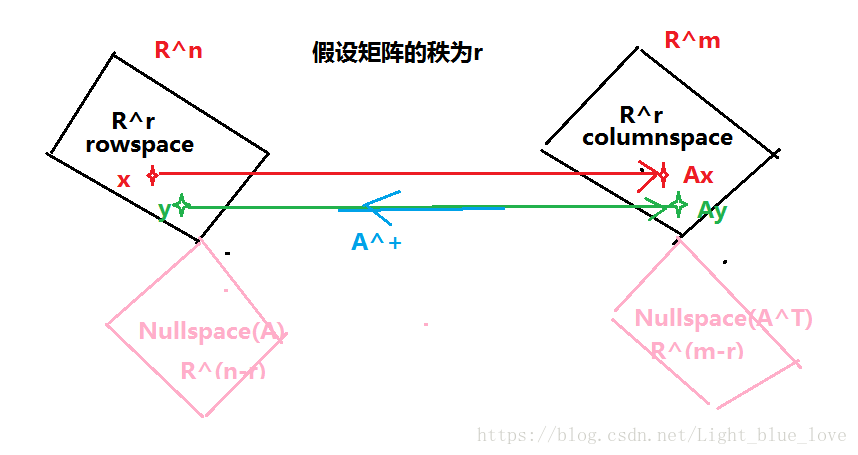
从上图中，在行空间中有两个向量$x$和$y$,$Ax$和$Ay$一定是在矩阵$A$的列空间中，那么这个矩阵$A$有点类似于行空间到列空间的一个映射。即行空间与列空间是一一对应的。如果向量$k$在矩阵$A$的零空间中，那么$Ak=0$,所以在整个$R^n$中的所有向量均可以由行空间中的向量和零空间中的向量表示。由于零空间的存在它会把这些向量变为零向量。这样所有$R^n$中所有向量便都被包含了。

所有空间中的向量都能由行空间中的分量和零空间中的分量组成，变换会将零空间中的分量消掉。

---

证明：矩阵$A$行空间中的向量$x,y$,如果$x\neq y$,那么$Ax\neq Ay$.
矩阵$A$为行空间到列空间的一个映射，如果我们就限制在这两个空间上，那么矩阵$A$就是可逆的，因为$Ax$,从行空间到了列空间，也可以由办法找到从列空间到行空间的映射。即$y=A^{\dagger}Ay$。伪逆$A^{\dagger}$的作用就是把$N(A^T)$变没。

现在假设$Ax=Ay$,那么$A(x-y)=0$,其中$x-y$属于$N(A)$。前假设向量$x,y$都在行空间中，那么$x-y$必然也在行空间中。因此出现矛盾，得出$x=y$。

---

怎么样得出伪逆$A^{\dagger}$
前面我们学到分解一个矩阵可以通过SVD方法来$A=U\Sigma V^T$。

其中对角阵$\Sigma = \begin{bmatrix}\sigma_1\\&\sigma_2\\&&\ddots\\&&&\sigma_r\\&&&&0\\&&&&&0\end{bmatrix}$。

那么这个矩阵的伪逆$\Sigma^{\dagger} = \begin{bmatrix}\frac{1}{\sigma_1}\\&\frac{1}{\sigma_2}\\&&\ddots\\&&&\frac{1}{\sigma_r}\\&&&&0\\&&&&&0\end{bmatrix}$。

$\Sigma \Sigma^{\dagger}= \begin{bmatrix}1\\&1\\&&\ddots\\&&&1\\&&&&0\\&&&&&&\ddots\end{bmatrix}$这是在列空间上的投影矩阵。

$\Sigma^{\dagger} \Sigma= \begin{bmatrix}1\\&1\\&&\ddots\\&&&1\\&&&&0\\&&&&&&\ddots\end{bmatrix}$这是在行空间上的投影矩阵。

矩阵可能没有左逆或者右逆，但是它一定存在伪逆。

$A^{\dagger}=V\Sigma^{\dagger}U^T$