MIT 18.06 linear algebra 第三十讲笔记
- Singular value Decomposition
- is diagonal U,V is Orthogonal
对称的正定矩阵 ,可以被写为 。正定矩阵的这种分解其实就是 分解的一种特例。而 分解并不需要 和 相等。
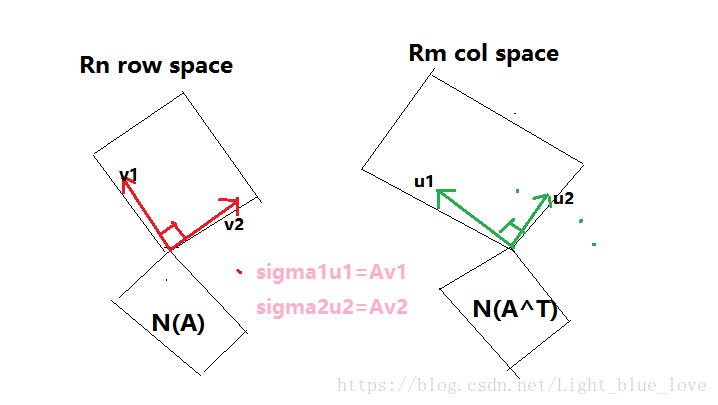
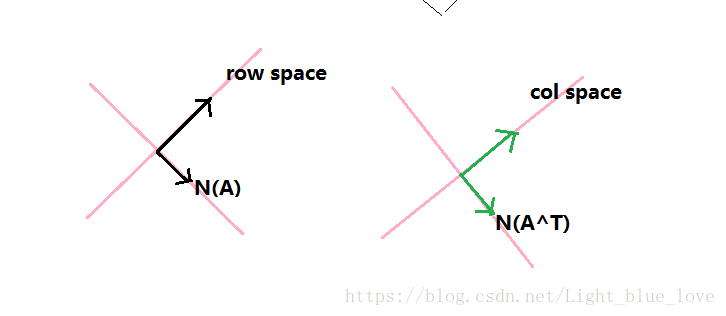
在上图中在行空间中选择一个单位向量 ,然后在列空间中使得存在单位向量 满足 。其中的 是一个数字,表示他们之间的数量关系。在找一个与 正交的单位向量 ,然后使得在列空间中存在一个与 正交的单位向量 满足 。通过史密斯正交法就可以找到一组标准正交的单位向量。
用矩阵表示也就是:
需要对上面的矩阵做一下说明,其中
是矩阵
行空间的一组标准正交基。如果矩阵
不是列满秩的话,需要增加矩阵
零空间的一组标准正交基。同理
是列空间的一组标准正交基,如果矩阵
不是行满秩的话,需要用
的零空间中的一组标准正交基来填充。其中
是
的一组标准正交基,
是
的一组标准正交基思考一下就会知道,如果存在零空间了,那么就需要找出零空间的一组标准正交基,那么
就会得到零,那么零就会出现在对角阵
的末尾。
求解时,
,那么
。
看到这里是否会突然联想到 。对于 对应的是正定或者至少半正定矩阵。 可以应对长方形矩阵。
例子
,可以看出这个矩阵是可逆的,因此设行空间的标准正交基为
,
为列空间的标准正交基。满足
和
。
,因此解出特征值为32和18,特征向量分别为 和 ,由于求出了矩阵 相应的矩阵 其实也就确定了,不能随便选取。 , ,可以代进去算一下,是正确的 。
我们可以通过
的方法来计算
,
。
与
的特征值是相同的,假设
,有
。
例子2
矩阵 ,此时行空间与列空间只是一维的因此需要添加零空间的正交基来补全。
此时对角阵就会出现用零填充的情况。按照上面的逻辑计算即可。