MIT 18.06 linear algebra 第二十七讲笔记
- Complex inner products
- Vector
- Matrices
- Discrete Fourier
- Fourier Matrix
Fn
- Fast Transform =
FFT
一个普通的
n
阶矩阵和一个向量做乘法时需要进行
n2
次乘法运算。而进行快速傅里叶变换后可以降低到
nlogn2
次。
如果有一个复数向量,那么求向量长度时:
||Z||2=[x1¯¯¯¯¯x2¯¯¯¯¯⋯xn¯¯¯¯¯]⎡⎣⎢⎢⎢⎢z1z2⋮zn⎤⎦⎥⎥⎥⎥
。这里是与实数向量不一样的。也就是说求一个复数向量长度的时候,需要以其共轭向量的转置乘以它。即
||Z||2=Z¯¯¯¯TZ
。
计算复数向量的内积时,假设计算
y
与
x
的内积时,公式为
y¯¯¯Tx=yHx
。其中的
H
的作用就是求其共轭并转置,此处
H
的英文为
Hermitian
。
在实数矩阵时,我们关于对称阵的定义为
AT=A
,但是这对复数矩阵不适用。关于复数对称矩阵的定义为
A¯¯¯¯T=A=AH
。这也意味着复数对称矩阵的对角线元素均为实数。例如
[23−i3+i5]
,这种矩阵又称为埃尔米特矩阵(又称“自共轭矩阵”)是共轭对称的方阵。满足
AH=A
这些矩阵的特征值为实数。
复数标准正交向量
q1,q2,⋯,qn
垂直,那么满足
qi¯¯¯¯Tqj{0ifi≠j1ifi=j
。
标准正交矩阵
Q
满足
Q¯¯¯¯TQ=I
。即
QHQ=I
。这种矩阵又称为酉矩阵,酉矩阵是正交矩阵往复数向量上的推广。
n
阶傅里叶矩阵
⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢111⋮11ww2⋮wn−11w2w4⋮w2(n−1)⋯⋯⋯⋱⋯1wn−1w2(n−1)⋮w(n−1)2⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥
。这个矩阵满足
(Fn)ij=wi∗j
,其中
i,j=0,1,⋯,n−1
。
如果有
wn=1
,那么
w=ei2πn
。
w=cos(2πn)+isin(2πn)
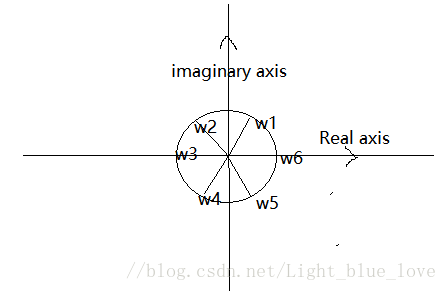
上面是
w6=1
。
当
n=4
时,
w4=1
,
w=eiπ2=i
,
i2=−1,i3=−i,i4=1
。因此
F4=⎡⎣⎢⎢⎢⎢11111ii2i31i2i4i61i3i6i9⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢11111i−1−i1−11−11−i−1i⎤⎦⎥⎥⎥
。通过这个
4×4
的矩阵可以得到一个4点的傅里叶变换。
上面的矩阵乘以
12
后就是一个酉矩阵,即
12F4
为酉矩阵。
当有
w64=1,w32=1
,那么
w264=w32
。我们可以将
F64
变换为关于
F32
的。
[F64]=[IID−D][F3200F32][p]
。以前
F64
乘以一个向量需要做
64×64
次乘法操作,现在只需要
2(32)2+fix
,其中fix是关于左右两侧关于修正矩阵的计算量。
其中右侧的修正矩阵是一个就置换矩阵,形如
p=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢111111⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥
。当
p
乘以一个向量,它能把所有奇数位置的分量统统排列到偶数分量之前。其中
D=⎡⎣⎢⎢⎢⎢⎢⎢⎢1ww2⋱w32⎤⎦⎥⎥⎥⎥⎥⎥⎥
。现在的计算量为
2(32)2+32
,其中乘以
I
和
p
都不需要大量的计算开销。
F32
又可以进一步分解
[F64]=[IID−D][F3200F32][p]=[IID−D]⎡⎣⎢⎢⎢IID−DIID−D⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢F16F16F16F16⎤⎦⎥⎥⎥[pp][p]
。
现在的计算量变为
2[x×162+16]+32
,如果像这样依次展开,左右两边扩展为修正矩阵,由于
log642=6
,因此左右各有6个修正矩阵。一共
log642∗642
。也就是计算公式为
logn2∗n2
。
假设现有有一个1024*1024维度的矩阵,那么它乘以一个向量计算量为1024*1024,但如果对其进行分解后,那么计算量为5*1024。降到了原来的
1200
.