再读线性回归 Linear Regression

1. 问题的回顾

线性回归（Linear Regression）是机器学习中的基本回归方法之一（其他的类似岭回归，多项式回归都是以之为基础）。简单的来讲，线性回归通过构造一个带有参数的多项式来预测新样本的值。如针对一个 $n$维向量 $x=(x_1;x_2;...;x_n)$，我们通过如下回归函数来预测 $x$ 的值，

$f_{\theta}(x) = \theta_{0} + \theta_{1}x_{1} + \theta_{2}x_{2} + ... + \theta_{n}x_{n}$

我们沿用吴恩达的一些经典标记法¹，如 $X=(x^{(1)};x^{(2)};...;x^{(m)})$ 以矩阵的形式表示一个拥有 $m$个样本的特征集，其中 $x^{(i)}$表示训练集中的第 $i$个样本， $Y=(y^{(1)};y^{(1)};...;y^{(m)})$ 以矩阵的形式表示一个特征集对应的值的集合， $y^{(i)}$表示 $i$个样本对应的值， $x_{j}^{(i)}$表示第 $i$个样本的第 $j$个特征， $\theta$ 表示回归函数中的参数组合，即 $\theta=(\theta_0;\theta_1;...;\theta_n)$。请注意，这里的参数集合有 $(n+1)$ 个元素。根据因此上述回归函数也可以写成矩阵相乘的形式，

$f_{\theta}(x^{(i)}) = (\theta_0, \theta_1, ... , \theta_n) \times \begin{pmatrix} 1 \\ x^{(i)}_1 \\ x^{(i)}_2 \\... \\ x^{(i)}_n \end{pmatrix} =\theta^T \times (1;x^{(i)})$

有上式可知，针对于每一组 $\theta$，每一个样本 $x^{(i)}$ 的都可以计算出其对应的预测值，即 $f_{\theta}(x^{(i)})$。我们定义一个模型的评价标准，即代价函数（也叫损失函数）

$J(\theta)= \frac{1}{2m} \sum_{i=1}^{m} (f_{\theta}(x^{(i)})-y^{(i)})^2$

当预测值与真实值的差距较小时，代价较小，表示模型性能较好且几乎能准确的预测所有的 $x^{(i)}$；反之，但预测值与真实值的差距较大时，代价越大，则表示训练出来的模型较差，不能够准确的预测。

因此，线性回归的问题可以看做是：找寻最佳参数组合 $\theta$ 使得整体的代价 $J(\theta)$ 值最小，也即 $\mathop{\arg\min}\limits_{\theta} J(\theta)$，也可写作，

$\mathop{\arg\min}\limits_{\theta} \frac{1}{2m} \sum_{i=1}^{m} (f_{\theta}(x^{(i)})-y^{(i)})^2$

于是问题来到了如何选取 $\theta$ 组合，使得 $J(\theta)$ 达到最小值。这里有两个方法可供考虑，一个是梯度下降（Gradient Descent），另一个就是最小二乘法（Least Square Method）。前者在梯度的指引下步步逼近最优参数，后者通过正规方程直接接触最优参数。两种方法也各有优缺点，这里我们只讨论梯度下降算法。

2. 梯度下降算法

想必大家都有登山的经历，在攀登完山顶领略到景色后，找到一条合适下山路十分重要。于是乎，人们一般都这样做：走了一段路后，观察一下周围，寻找最优的下山效率的路，接着再走一段路。周而复始，直至到达地面。如果我们定义下山效率为，

$下山的效率 = \frac{人行走的距离}{下降的海拔高度}，单位时间 t 内$

可以想见，下山效率最快的路在单位时间内下降的海拔最多。一旦你走错了方向，则下降海拔高度为负数，那么效率也变成了负数。只有我们走对了方向，且在对的方向上下降的最快，这样，我们才能迅速准去的到达地面。

线性回归的过程也可以类比成下山的过程，例子中的海拔高度就是要优化的代价函数 $J(\theta)$，地面就是代价函数 $J(\theta)$ 的最优点（先不考虑局部最优的问题），下山的路就是回归参数 $\theta$，每次选择的方向就是梯度。学过微积分的朋友一定知道，对以 $\theta$ 为变量的代价函数 $J(\theta)$ 而言，梯度就是代价函数对于每个 $\theta$ 的偏导数的组合 ，因此，梯度 $\nabla J(\theta)$ 可表示为，

$\nabla J(\theta) = (\frac{\partial J(\theta)}{\theta_0}, \frac{\partial J(\theta)}{\theta_1},..., \frac{\partial J(\theta)}{\theta_n})$

总之，我们只需要明白：“沿着梯度 $\nabla J(\theta)$ 的方向下降， $J(\theta)$ 下降的最快。”

在迭代地更新参数 $\theta$，这时候需要引入另一个概念：学习率 $\alpha$。形象的来讲，梯度决定了参数每次更新的方向，而学习率则决定了参数每次更新的程度。一般的学习率的设定因问题而定，一般会设为 $\{0.1,0.01,0.001\}$ 等值。

有了学习率和梯度，我们就可以定义参数更新的过程了，对于每个参数 $\theta_j$ 而言，有如下计算公式，根据这个公式，通过步步迭代，我们就可以计算出最终的 $\theta=(\theta_0; \theta_1;...;\theta_n)$ 了。

$\theta_j = \theta_j - \alpha \times \frac{\partial J(\theta)}{\partial \theta_j} =\theta_j - \alpha \times \frac{1}{m}\sum_{i=1}^{m}(f_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_j$

上述等式中 $\alpha$ 的后半部分其实就是 $J(\theta)$ 对于 $\theta_j$ 的偏导数，为了便于矩阵计算，我们也可以写作如下的形式，有兴趣的也可以推一推，其实很简单。

$\theta = \theta - \alpha \times \frac{1}{m}\sum_{i=1}^{m}(f_{\theta}(x^{(i)})-y^{(i)})x^{(i)}$

最后，整体的线性回归过程可以归纳为，

def Linear_Regression_Algorithm(train_x, train_y):
	'''
	线性回归整体框架
	Parameters
	--------------
	:train_x: 原始特征集合（mxn）
	:train_y: 原始标签集合（nx1）
	
	Returns
	--------------
	:theta: 最佳参数（(n+1)x1）
	'''
	# 初始化学习率 theta，初始化学习率 eta，最大迭代次数 loop
	train_x, theta, alpha, loops = initalize() 
	# 计算初始代价
	cost = compute_cost(theta, train_x, train_y) 
	# 迭代更新参数
	while loop >0: 
		if cost == 0: # 如果达到最优，直接跳出循环
			break 
		# 更新参数
		theta = update_parameters(theta, alpha, train_x, train_y)
		# 计算代价
		cost = compute_cost(theta, train_x, train_y) 
		loops -= 1
		
	return theta

具体的函数实现为 initialize(), compute_cost(), 和 update_parameters()如下所示（需将 numpy 包导入）。

imort numpy as np
def initialize(train_x):
	'''
	初始化线性回归模型的超参数，包括学习参数，学习率，循环次数等
	
	Parameters
	-------------
	:train_x: 原始特征集合
	
	Returns
	-------------
	:多返回值: train_x, theta, alpha, loops
	'''
	n = len(train_x[0])
	theta = np.random.randn(n+1,1) # parameters vector
	alpha = 0.005 # learning rate
	loops = 5000 # maximum loop number
	train_x = np.insert(train_x, 0, values=1, axis=1)

	return train_x, theta, alpha, loops


def compute_cost(theta, train_x, train_y):
	'''
	计算给定参数的代价值，即均方差.

	Parameters
	---------------
	:theta: 参数向量
	:train_x: 特征集合
	:train_y: 标签集合

	Returns
	---------------------
	:cost: 计算的代价值
	'''
	m = len(train_y)

	sub_matrix = train_x.dot(theta)-train_y
	cost = sub_matrix.T.dot(sub_matrix)[0][0]/(2*m)

	return cost


def update_parameters(theta, train_x, train_y, alpha):
	'''
	更新学习参数组合 theta.
	
	Parameters
	--------------------
	:theta: 参数向量
	:train_x: 特征集合
	:train_y: 标签集合
	:alpha: 学习率
	
	Returns
	---------------------
	:theta: 更新后的参数向量
	'''
	m = len(train_y)
	n = len(train_x[0])
	for i in range(m):
		theta -= (alpha/m)*((train_x[i]*theta)[0][0]-train_y[i][0])*(np.reshape(train_x[i], (n,1)))

	return theta

3. 一个简单的例子

假设 $x^{(i)}$ 是一维向量，那么我们要解决的问题就是：给定训练特征 $X$ 及其标签值 $Y$，寻找最合适的多项式方程 $f_{\theta}(x)$ 。由于 $x^{(i)}$ 是一维向量，故我在1.3节里省去表示特征维度的下标 $j$，即 $x^{(i)}$ 等价于 $x^{(i)}_j$。

$f_{\theta}(x^{(i)}) = \theta_0 + \theta_1x^{(i)}$

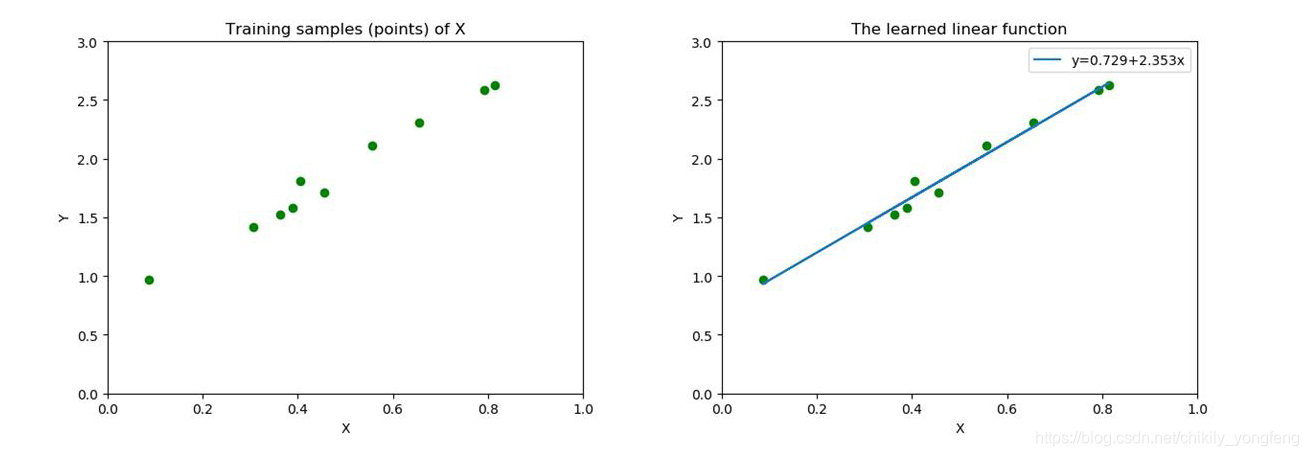
这样一来，我们的线性回归问题就可以看做是寻找一条线来拟合坐标上的点，如下图所示，左图是一些散列的点，表示我们的训练样本。右图展示了最终线性回归的结果，表示拟合的直线。根据算法，我们得到了最佳的函数 $y=0.729+2.353x$，该函数拟合的效果最好。现在我们来一步步推导出这个最佳函数的陈胜国成

首先，根据 $J(\theta)$ 的定义，我们将代价函数简化为，

$J(\theta) = \frac{1}{2m} \sum_{i=1}^m(\theta_0 + \theta_1x^{(i)} -y^{(i)}))^2$

在 $J(\theta)$ 函数中， $\theta_1,\theta_2$ 才是 $J(\theta)$ 的变量，而我们将 $x,y$ 看作是常数，因为具体的样本特征和标签值已知，即 $X,Y$ 已知。 我们将所有的 $X,Y$ 中的数据带入到 $J(\theta)$ 中去，会得到参数与代价函数之间的三维曲面图²。曲面的最低点，就是我们要找的最优 $\theta_1,\theta_2$ 的值。因此线性回归的做法相当于，首先在曲面上随机选取一个点，然后沿着梯度的方向慢慢向最低点移动，直到到达最低点。

事实上，不同的 $\theta$ 组合可能导致相同的代价值 $J(\theta)$，下面右图的等高线图³ 就反映了这一点，在每一条等高线上的 $\theta_0,\theta_1$ 的值造成的代价是相同的。其实等高线图可以看做是左侧曲面图的横截面，每一个面的边缘对应的参数取值造成的效果是相同的。

具体地，通过对 $J(\theta)$ 求偏导，我们得到参数 $\theta_0,\theta_1$ 的更新方法如下，

$\frac{\partial J}{\partial \theta_0} = \frac{1}{m}\sum_{i=1}^{m}(\theta_0 + \theta_1x^{(i)}-y^{(i)})， x^{(i)}\in X, y^{(i)}\in Y \\ \frac{\partial J}{\partial \theta_1} = \frac{1}{m}\sum_{i=1}^{m}(\theta_0 + \theta_1x^{(i)}-y^{(i)})x^{(i)}， x^{(i)}\in X, y^{(i)}\in Y$

因此在每一轮迭代更新中，我们都用计算出 $\frac{\partial J}{\partial \theta_0}$ 和 $\frac{\partial J}{\partial \theta_1}$ 的值，因此我们每一轮更新参数，如下所示。

$\theta_0 = \theta_0-\alpha\frac{\partial J}{\partial \theta_0} \\ \theta_1 = \theta_1-\alpha\frac{\partial J}{\partial \theta_1}$

4. 一些细节

在实现线性回归的过程中，最重要的就是初始参数的选择，也就是学习率 $\alpha$ 和参数向量 $\theta$。

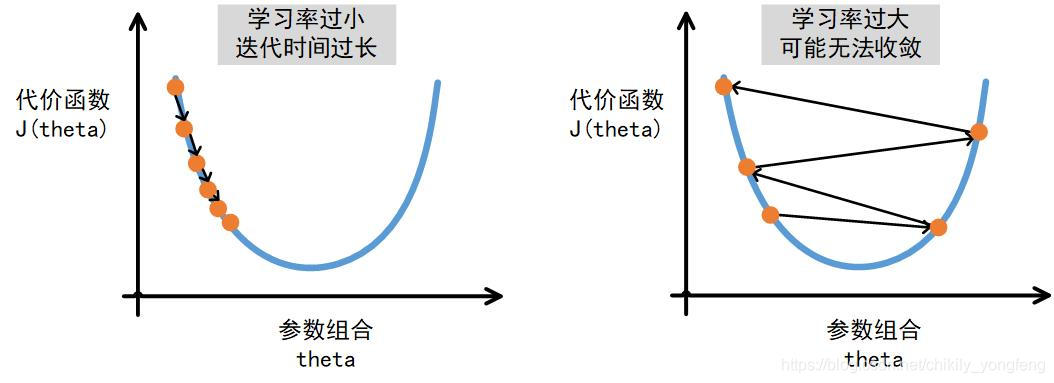
对于 $\alpha$ 而言，一方面， $\alpha$ 设置的太小会导致梯度下降算法收敛变慢。另外，梯度下降算法在逼近最优解的过程中，由于梯度的减小，逼近速度本身会越来越慢。此时如果 $\alpha$ 再小，那就是龟速了。另一方面， $\alpha$ 设置的太大，可能会让算法无法收敛，一个典型的例子就是，代价函数越来越大。

对于 $\theta$ 而言，不同的初始化方法会产生不同的结果，由于实际处理的问题，代价函数可能拥有多个局部最优解，常见的初始化方法有：随机均匀分布，随机高斯分布，随机泊松分布等，这些随机化的方法给参数 $\theta$ 赋予了不同的初始值，因此极有可能造成不同的结果，因此合适取值的才是最好的取值。

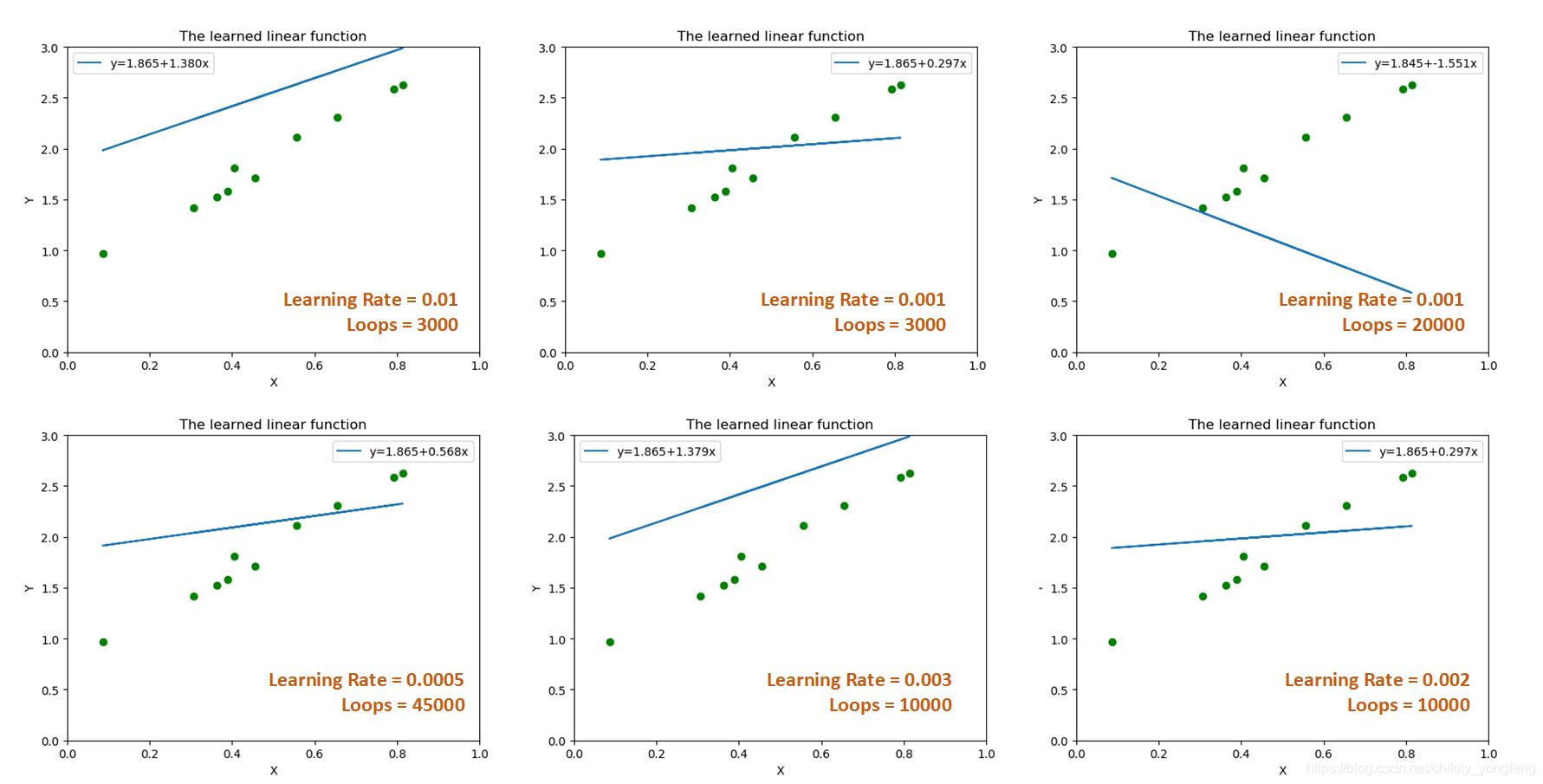
下面 6 张图是针对第 3 节中设置不同参数组合的结果，可以看到不同的组合造成的效果不一样。这其实也是线性回归的一个“缺点”吧，训练结果对于参数十分敏感，如何调整参数来确保最佳的拟合效果仍然值得进一步探讨。

5. SKLearn 提供的算法包

Sklearn 包⁴也提供了线性回归模型的简易接口，调用起来很方便，相对应的代码段如下，

from sklearn.linear_model import LinearRegression

def sklearn_linearRegression(train_x, train_y):	
	reg = LinearRegression().fit(train_x, train_y)	# 训练
	# reg.coef_ 记录了每个特征前的参数，即 theta_1, theta_2,...,theta_n
	# reg.intercept_ 记录了截距，即 theta_0
	reg.predict(tran_x) # 预测

最终，Sklearn 包得到的效果是非常好的，基本拟合了各个样本点。这个根本原因是 Sklearn 包计算参数的方法不是梯度下降，而是我后面想要介绍的 最小二乘法。需要指出的是，在大部分情况下（数据维度在 10000 以下），梯度下降都比最小二乘法的效果要差，但是这并不说明最小二乘法是万能的，它也有自己的缺陷。我们在使用的时候需要针对实际情况来做出选择。

---

1. 网易云课堂. “吴恩达机器学习”（视频）. Link ↩︎

2. Eddy_zheng. 绘制三维图形、三维数据散点图. Link ↩︎

3. Mr-Cat伍可猫. 用 matplotlib contour 画等高线图. Link ↩︎

4. Sklearn. LinearRegression. Link ↩︎