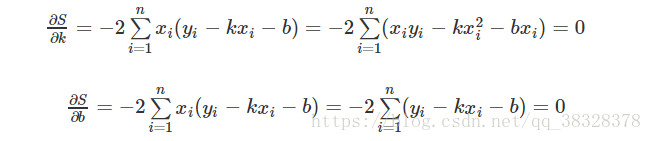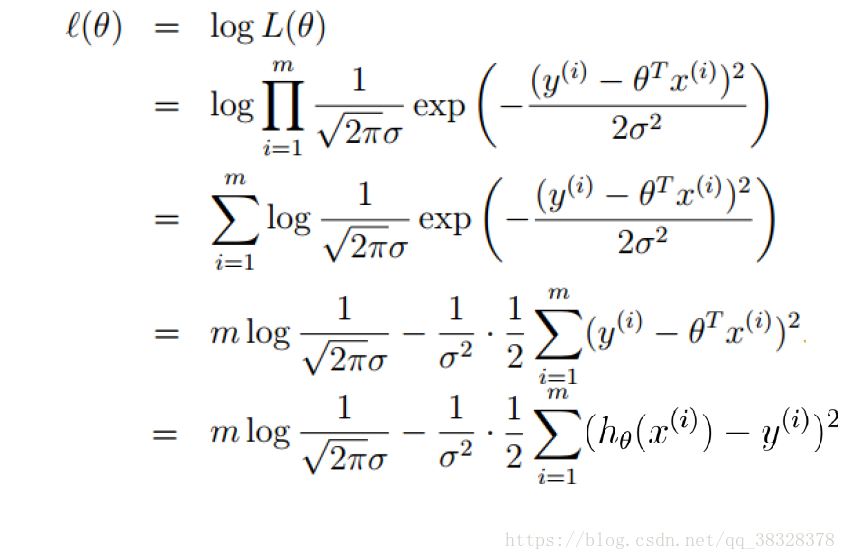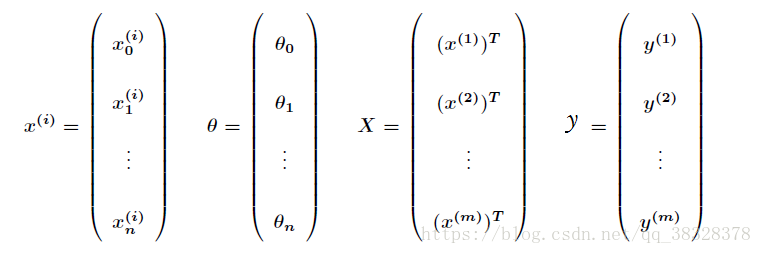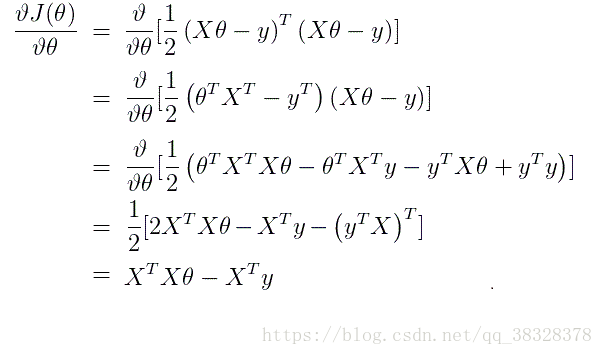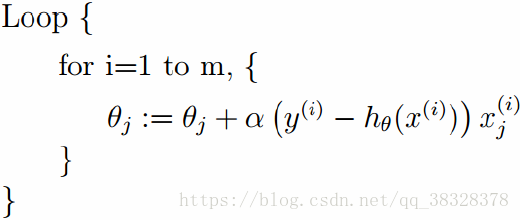Python机器学习 — 线性回归（Linear Regression）

线性回归 -- 简介

线性回归是机器学习算法中最简单的算法之一，它是监督学习的一种算法，主要思想是在给定训练集上学习得到一个线性函数，在损失函数的约束下，求解相关系数，最终在测试集上测试模型的回归效果。

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w'x+e，e为误差服从均值为0的正态分布。

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

线性回归分析

简单线性回归：一个解释变量

多元线性回归：多个解释变量

线性回归 -- 步骤

回归分析的步骤：

1、根据预测目标，确定自变量和因变量；

2、绘制散点图，确定回归模型类型；

3、估计模型参数，建立回归模型；

4、对回归模型进行检验；

5、利用回归模型进行预测；

线性回归 -- 简单线性回归

一元回归的主要任务是从两个相关变量中的一个变量去估计另一个变量，被估计的变量，称因变量，可设为Y；估计出的变量，称自变量，设为X。回归分析就是要找出一个数学模型Y=f(X)，使得从X估计Y可以用一个函数式去计算。当Y=f(X)的形式是一个直线方程时，称为一元线性回归。这个方程一般可表示为Y=A+BX。根据最小平方法或其他方法，可以从样本数据确定常数项A与回归系数B的值。A、B确定后，有一个X的观测值，就可得到一个Y的估计值。回归方程是否可靠，估计的误差有多大，都还应经过显著性检验和误差计算。有无显著的相关关系以及样本的大小等等，是影响回归方程可靠性的因素。

现实世界中的数据总是存在各种误差，比如测量工具的误差，人度数的误差等等。而且数据的产生也大部分是一个随机的过程。所以如果现实世界中存在某些线性关系，那么这个关系也一定是近似的。所以其一次函数其实是这样的：
$\small y=kx+b+e$
其中 $\small e$ 是数据偏离线性的误差，这个误差是服从正态分布的。什么！你还不知道什么是正态分布？那请先学习下相关知识。就是因为这个 $\small e$ 的存在，所以对于每一组数据 $\small \left ( x,y \right )$ ，他们的误差都是不同的，所以在前面那个式子中，我们不能使用待定系数法求得尽量精确的解。所以就需要一个更高端的做法。

线性回归的方法

为了求解出最小的 $\dpi{150} \small \sum_{i=1}^{n}\left |e _{i} \right |$ ，我们可以其实可以利用平方消去其中的绝对值符号，得到了我们的要求的式子：

$\small S=\sum_{i=1}^{n}e^{2}=\sum_{i=1}^{n}\left (y _{i} \right-kx_{i}-b )^{2}$

为了取到最小的S，我们可以对上式分别对 $\small k$ 和 $\small b$ 求偏导，并令它们为 $\small 0$ ，以求的S的极值。

根据这个式子，可以知道偏导数的图像（如左图）和原函数随 $\small k$ 或者 $\small b$ 变化的图像（类似于右图）

所以可以说，当这两个偏导数都取到 $\small 0$ 的时候，就是误差 $\tiny \sum e^{2}$ 取到最小值的时候。现在将 $\small k$ 和 $\small b$ 提取出来

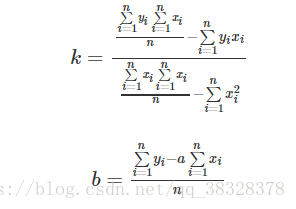
算法实现

#根据y=2*x+b随意写几个数
X=[1,2,3,4,5,6,7]
Y=[3.09,5.06,7.03,9.12,10.96,12.91,15.01]
Xsum=0.0
X2sum=0.0
Ysum=0.0
XY=0.0
n=len(X)
for i in range(n):
    Xsum+=X[i]
    Ysum+=Y[i]
    XY+=X[i]*Y[i]
    X2sum+=X[i]**2
k=(Xsum*Ysum/n-XY)/(Xsum**2/n-X2sum)
b=(Ysum-k*Xsum)/n
print('the line is y=%f*x+%f' % (k,b) )

线性回归 -- 多元线性回归

在回归分析中，如果有两个或两个以上的自变量，就称为多元回归。事实上，一种现象常常是与多个因素相联系的，由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。因此多元线性回归比一元线性回归的实用意义更大。

二元线性回归

设 $\large h_{\theta }\left ( x \right )$ 为因变量， $\large x_{1},x_{2}$ 为自变量，并且自变量与因变量之间为线性关系时，则二元线性回归模型为：

$\large h_{\theta }\left ( x \right )=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}$

多元线性回归

假设 $\large h_{\theta }\left ( x \right )$ 为因变量， $\large x_{1},x_{2},...,x_{n}$ 为自变量，并且自变量与因变量之间为线性关系时，则多元线性回归模型为：

$\large h_{\theta }\left ( x \right )=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+...+\theta _{n}x_{n}+\varepsilon$

其中 $\large h_{\theta }\left ( x \right )$ 为因变量， $\large x_{i}\left ( i=1,2,...,n \right )$ 为n个自变量， $\large \theta _{i}\left ( i=0,1,...,n \right )$ 为 $\large n+1$ 个未知参数， $\large \varepsilon$ 为随机误差项。

假设随机误差项 $\large \varepsilon$ 为0时，因变量 $\large h_{\theta }\left ( x \right )$ 的期望值和自变量 $\large x_{1},x_{2},...,x_{n}$ 的线性方程为：

$\large h_{\theta }\left ( x \right )=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+...+\theta _{n}x_{n}=\sum_{i=0}^{n}\theta _{i}x_{i}=\theta ^{T}x$

从下图来直观理解一下线性回归优化的目标——图中线段距离（平方）的平均值，也就是最小化到分割面的距离和。

线性回归模型 -- 最小二乘法

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

使用极大似然估计解析最小二乘法：

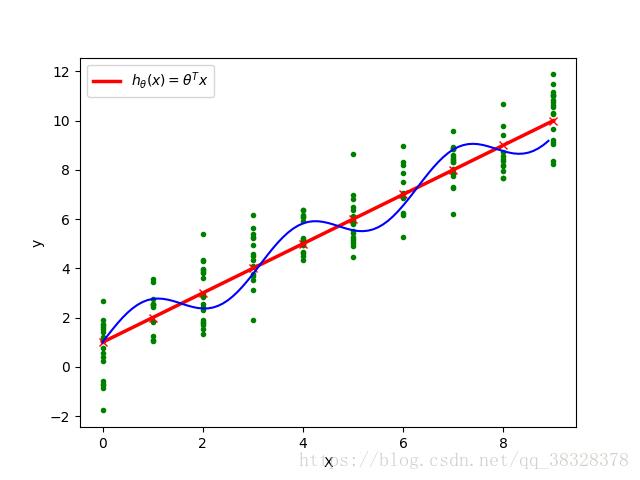
$\large \bg_white \small J(\theta) = \frac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2$

　　在真实数据中，一个x值可能对应多个y值，因为实际y值可能是受多种因素影响，所以我们可以假设任意一个x对于的y的真实值服从正态分布。我们什么时候可以认为模型 $\small h_\theta(x)$ 拟合出来的点最好？当然是 $\large \bg_white \large \bg_white \large \small h_\theta(x)$ 取值概率最大的时候。

如上图，红蓝两条线来拟合绿色的这些数据点，明显红色的直线拟合效果更好一些。为什么？仔细看图中直线上红色x点，红色的x点正好是当前x值下，训练数据中出现概率最高的位置（之前我们已经假设每个位置y值符合高斯分布）。所以我们要求的就是使得拟合出的线(高纬度是超平面)上概率最大的 $\large \theta$ ，这个时候我们就可以用到极大似然估计。
　　接下来我们用极大似然来证明最小二乘法。假设误差 $\large ε^{(i)} (1≤i≤m)$ $\large ε^{(i)} (1≤i≤m)$ $\large ε^{(i)} (1≤i≤m)$ $\large ε^{(i)} (1≤i≤m)$ $\large (\varepsilon )^{i}\left ( 1\leq i\leq m \right )$ （就是上图中绿色数据点到红色x点的距离）是独立同分布的，服从均值为0，方差为某定值 $\large \sigma^2$ 的高斯分布。

可以得到似然函数：

$\large y^{(i)} = \theta^T x^{(i)} + \epsilon^{(i)}$

$\large \epsilon^{(i)}$ 的正态分布公式：

$\large p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(\epsilon^{(i)})^2}{2\sigma^2}}$

将似然公式带入正态分布公式，得到：

$\large p(\epsilon^{(i)})= \frac{1}{\sqrt{2\pi}\sigma}e^{(-\frac{(y^{(i)}-\theta^Tx{^{(i)}})^2}{2\sigma^2})}$

m个样本是独立的，进行下面的运算得到关于 $\large \theta$ 的似然函数 $\large L\left ( \theta \right )$ ：

对上面似然函数求对数得到对数似然函数 $\large \ell(\theta)$

上式中， $\large \sigma$ 是定值，我们要使得上式最大，就得使 $\large \frac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2$ 最小，于是我们就得到了线性回归的目标函数：

$\large J(\theta) = \frac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2$

其实通过这个公式我们可以求得关于 $\large \theta$ 的解析解，可以直接计算出 $\large \theta$ ，但我们一般不这么做，因为求解析解过程中需要求矩阵的逆，这是一个非常耗时的工作（时间复杂度 $\large \Theta(n^3)$ ），另外矩阵也不一定可逆，一般都是用梯度下降。但我们还是看下如何求 $\large \theta$ 的解析解。

将M个N维样本组成矩阵X：

· X的每一行对应一个样本，共M个样本（measurements）；

· X的每一列对应样本的一个维度，共N维（regressors）;

· 还有额外的一维常数项，全为1；

根据上矩阵，可以得到 $\large X\theta -y$ ：

目标函数，即损失函数：

$\small J\left ( \theta \right )=\frac{1}{2}\sum_{i=1}^{m}\left ( h_{\theta }\left (x ^{\left ( i \right )} \right )-y^{\left ( i \right )} \right )^{2}=\frac{1}{2}\left ( X\theta -y \right )^{T}\left ( X\theta -y \right )$

对 $\tiny J\left ( \theta \right )$ 求一阶导得到梯度。

求 $\tiny J\left ( \theta \right )$ 导数最小值，即求导数为零的点（驻点）：

$\large \frac{\vartheta J\left ( \theta \right )}{\vartheta \theta }=X^{T}X\theta -X^{T}y=0$

上述得到的方程组叫做正规方程组，那么最终得到

$\large \theta =\left ( X^{T}X \right )^{-1}X^{T}y$

线性回归模型 -- 梯度下降算法

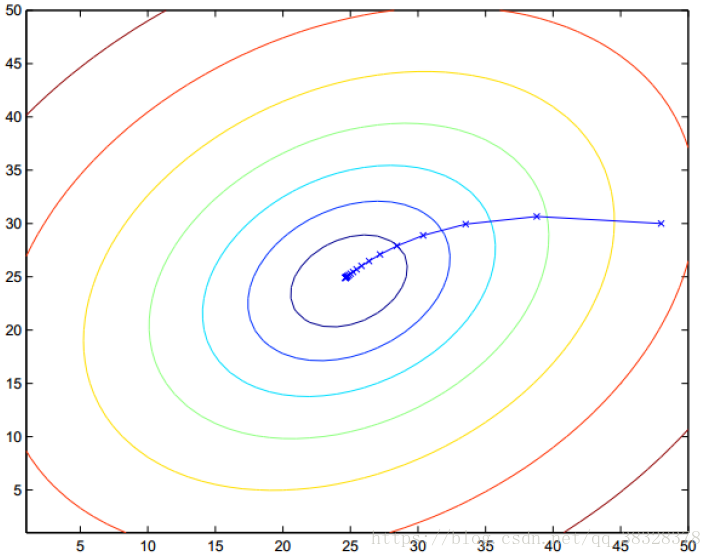
首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。

从上面的解释可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

梯度下降的相关概念

　　　　在详细了解梯度下降的算法之前，我们先看看相关的一些概念。

　　　　1. 步长（Learning rate）：步长决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度。用上面下山的例子，步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。

　　　　2.特征（feature）：指的是样本中输入部分，比如2个单特征的样本 $\large （x^{(0)},y^{(0)}）$ $\large \left ( x^{\left ( 0 \right )},y^{\left ( 0 \right )} \right )$ ， $\large \left ( x^{\left ( 1 \right )},y^{\left ( 1 \right )} \right )$ $\large （x^{(0)},y^{(0)}）,（x^{(1)},y^{(1)}）$ ，则第一个样本特征为 $\large x^{(0)}$ ，第一个样本输出为 $\large y^{(0)}$ 。

　　　　3. 假设函数（hypothesis function）：在监督学习中，为了拟合输入样本，而使用的假设函数，记为 $\large h_{\theta}(x)$ 。比如对于单个特征的m个样本 $\large \left ( x^{\left ( i \right )},y^{\left ( i\right )} \right )\left ( i=1,2,...,m \right )$ $\large （x^{(i)},y^{(i)}）(i=1,2,...m)$ ，可以采用拟合函数如下： $\large h_{\theta}(x) = \theta_0+\theta_1x$ 。

　　　　4. 损失函数（loss function）：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平方。比如对于m个样本 $\large \left (x_{i},y_{i} \right )(i=1,2,...m)$ ，采用线性回归，损失函数为：

$\large \bg_white \small J(\theta) = \frac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2$

　　　　其中 $\large x_{i}$ 表示第i个样本特征， $\large y_{i}$ 表示第i个样本对应的输出， $\large h_\theta(x_i)$ 为假设函数。

梯度下降的详细算法

　既然在变量空间的某一点处，函数沿梯度方向具有最大的变化率，那么在优化目标函数的时候，自然是沿着负梯度方向去减小函数值，以此达到我们的优化目标。

1. 先决条件：确认优化模型的假设函数和损失函数。

对于线性回归，假设函数 $\large h_\theta(x_1, x_2, ...x_n) = \theta_0 + \theta_{1}x_1 + ... + \theta_{n}x_{n}$ 的矩阵表达方式为： $\large h_\mathbf{\theta}(\mathbf{x}) = \mathbf{X\theta}$

其中，假设函数 $\large h_{\theta}(x)$ 为m*1的向量,θ为(n+1)*1的向量，里面有n个代数法的模型参数。X为m*(n+1)维的矩阵。m代表样本的个数，n+1代表样本的特征数。

损失函数的表达式为： $\large J(\mathbf\theta) = \frac{1}{2}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y})$ ，其中Y是样本的输出向量，维度为m*1.

2. 算法相关参数初始化

主要是初始化 $\large \theta_0, \theta_1..., \theta_n$ ，算法终止距离ε以及步长α。在没有任何先验知识的时候，我喜欢将所有的θ初始化为0，将步长初始化为1。在调优的时候再优化。

3. 算法过程

1）确定当前位置的损失函数的梯度，对于θ 向量，其梯度表达式如下：

$\large \frac{\partial}{\partial\mathbf\theta}J(\mathbf\theta)$

2）用步长乘以损失函数的梯度，得到当前位置下降的距离，即 $\large \alpha\frac{\partial}{\partial\theta}J(\theta)$ 对应于前面登山例子中的某一步。

3）确定θ向量里面的每个值，梯度下降的距离都小于ε，如果小于ε则算法终止，当前θ向量即为最终结果。否则进入步骤4.

4）更新θ向量，其更新表达式如下。更新完毕后继续转入步骤1.

　　　　　　　　 $\large \mathbf\theta= \mathbf\theta - \alpha\frac{\partial}{\partial\theta}J(\mathbf\theta)$

梯度方向

对 $\large J\left ( \theta \right )$ 进行关于 $\large \theta _{j}$ 的求导，得到梯度下降的梯度方向：

批量梯度下降法（Batch Gradient Descent）

批量梯度下降法，是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有的样本来进行更新，上面的详细算法过程就是使用批量梯度下降法实现的。对应的更新公式是：

由于我们有m个样本，这里求梯度的时候就用了所有m个样本的梯度数据。

批量梯度下降法图示：

随机梯度下降法（Stochastic Gradient Descent）

随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的m个样本的数据，而是仅仅选取一个样本j来求梯度。对应的更新公式是：

随机梯度下降法，和的批量梯度下降法是两个极端，一个采用所有数据来梯度下降，一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。对于准确度来说，随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。

线性回归 -- 实例

#线性回归
import numpy as np # 快速操作结构数组的工具
import matplotlib.pyplot as plt  # 可视化绘制
from sklearn.linear_model import LinearRegression  # 线性回归


# 样本数据集，第一列为x，第二列为y，在x和y之间建立回归模型
data=[
    [0.067732,3.176513],[0.427810,3.816464],[0.995731,4.550095],[0.738336,4.256571],[0.981083,4.560815],
    [0.526171,3.929515],[0.378887,3.526170],[0.033859,3.156393],[0.132791,3.110301],[0.138306,3.149813],
    [0.247809,3.476346],[0.648270,4.119688],[0.731209,4.282233],[0.236833,3.486582],[0.969788,4.655492],
    [0.607492,3.965162],[0.358622,3.514900],[0.147846,3.125947],[0.637820,4.094115],[0.230372,3.476039],
    [0.070237,3.210610],[0.067154,3.190612],[0.925577,4.631504],[0.717733,4.295890],[0.015371,3.085028],
    [0.335070,3.448080],[0.040486,3.167440],[0.212575,3.364266],[0.617218,3.993482],[0.541196,3.891471]
]

#生成X和y矩阵
dataMat = np.array(data)
X = dataMat[:,0:1]   # 变量x
y = dataMat[:,1]   #变量y

# ========线性回归========
model = LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
model.fit(X, y)   # 线性回归建模
print('系数矩阵:\n',model.coef_)
print('线性回归模型:\n',model)
# 使用模型预测
predicted = model.predict(X)

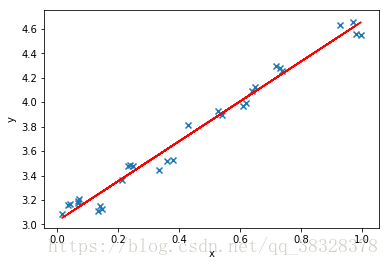
# 绘制散点图 参数：x横轴 y纵轴
plt.scatter(X, y, marker='x')
plt.plot(X, predicted,c='r')

# 绘制x轴和y轴坐标
plt.xlabel("x")
plt.ylabel("y")

# 显示图形
plt.show()

输出结果：

        系数矩阵:
                         [ 1.6314263]
        线性回归模型:

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

图形：