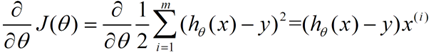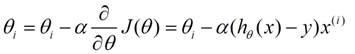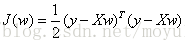在现实生活中普遍存在着变量之间的关系,有确定的和非确定的。确定关系指的是变量之间可以使用函数关系式表示,还有一种是属于非确定的(相关),比如人的身高和体重,一样的身高体重是不一样的。
线性回归:
1: 函数模型(Model):
假设有训练数据
那么为了方便我们写成矩阵的形式
2: 损失函数(cost):
现在我们需要根据给定的X求解W的值,这里采用最小二乘法。
a.最小二乘法:
何为最小二乘法,其实很简单。我们有很多的给定点,这时候我们需要找出一条线去拟合它,那么我先假设这个线的方程,然后把数据点代入假设的方程得到观测值,求使得实际值与观测值相减的平方和最小的参数。对变量求偏导联立便可求。
因此损失代价函数为:
3: 算法(algorithm):
现在我们的目的就是求解出一个使得代价函数最小的W:
a.矩阵满秩可求解时(求导等于0):

b.矩阵不满秩时(梯度下降):
梯度下降算法是一种求局部最优解的方法,对于F(x),在a点的梯度是F(x)增长最快的方向,那么它的相反方向则是该点下降最快的方向,具体参考wikipedia。
原理:将函数比作一座山,我们站在某个山坡上,往四周看,从哪个方向向下走一小步,能够下降的最快;
注意:当变量之间大小相差很大时,应该先将他们做处理,使得他们的值在同一个范围,这样比较准确。
1)首先对θ赋值,这个值可以是随机的,也可以让θ是一个全零的向量。
2)改变θ的值,使得J(θ)按梯度下降的方向进行减少。
描述一下梯度减少的过程,对于我们的函数J(θ)求偏导J:
Repeat until convergence:{
下面是更新的过程,也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值,-后面的部分表示按梯度方向减少的量,α表示步长,也就是每次按照梯度减少的方向变化多少。
}
假设有数据集D时:
对损失函数求偏导如下:
使用矩阵表示(方便计算)
从概率层面解释-回归模型的目标函数:
基本上每个模型都会有一个对应的目标函数,可以通过不同的最优化求解方法(梯度下降,牛顿法等等)对这些对应的目标函数进行求解。线性回归模型,我们知道实际上是通过多个自变量对自变量进行曲线拟合。我们希望找到一条可以较好拟合的曲线,
那我们如何判断一条曲线的拟合程度的好坏。上面讲到,我们采用的是最小二乘法(预测值和真实值得误差的平方和),那为什么要用这个作为目标函数呢?
可以从中心极限定理、高斯分布来分析:
1.中心极限定理:
设有n个随机变量,X1,X2,X3,Xn,他们之间相互独立,并且有相同的数学期望和均值。E(X)=u;D(x)=δ2.令Yn为这n个随机变量之和。
Zn为X这几个变量的规范和。
2.高斯分布
假的给定一个输入样本x,我们得到预测值和真实值间的存在的误差e,那么他们的关系如下:
而这里,我们就可以假设e服从标准的高斯分布。
为什么呢?回归模型的最终目标是建立自变量x和y之间的关系,我们希望通过x可以较为准确的表示结果y。而在实际应用场景中,很难甚至不可能把导致y结果的所有变量(特征)都找到,放到回归模型里面。
我们只存放那些认为比较重要的特征。根据中心极限定理,把那些对结果影响比较小的(假设独立分布)之和认为是符合正态分布是合理的。
那么x和y的条件概率:
那么知道一条样本的概率,我们就可以通过极大估计求似然函数,优化的目标函数如下:
通过取对数我们可以发现极大似然估计的目标函数和最小平方误差是一样。
在概率模型中,目标函数的极大和极小与极大似然估计是等价的。
假设随机变量为Y,和普通变量x存在相关关系,由于Y是随机变量,对于x的各个确定值,Y有它的分布(高斯)。
假设为:
使用极大似然估计可求解。
我们知道对于下面公式:

y为随机变量,在c=E(y)时达到最小,这表明以E(y)作为y的近似是最好的。
线性回归推导和总结
1. 线性模型的基本形式
我们将形式为f(x)=w1x1 +w2x2+...+wnxn+b的方程式称作线性方程。对于这个方程式,只要能求出w1、w2...wn和b,并代入x1、x2...xn,则可以求出对应的f(x)的值。
以上是线性方程式的描述,将此方程式转移到机器学习中的线性模型,描述如下:
由给定的n个特征值组成的特征集示例x=(x1;x2;...;xn),其中xi是x在第i个特征上的取值,线性回归模型的目标是通过学得w1、w2...wn和b,来准确预测f(x)的值。例如,银行根据一个人的年龄x1、工作收入x2、是否有房子x3来预测给这个人的贷款额度,假设此时的w1为0.3,w2为0.3,w3为0.4,b为1则有f(x)=0.3*x1+0.3*x2+0.4*x3+1。在这里wi即为相应特征的权重。
f(x)=w1x1 +w2x2+...+wnxn+b即成为线性模型,其中的b称为偏置项。此时,如果令w0为1,令x0为b,对该式进行整合,则一般用向量形式表示如下:
f(x) = wTx
2. 线性回归
通常在说线性回归之前,总是要搞清楚“分类”和“回归”这两个概念,这也是机器学习中很重要的概念。简单来讲,“分类”和“回归”都是预测目标值的过程,但是“分类”预测的是离散型变量,而“回归”预测的是连续型变量。还是用银行贷款的例子来说:银行是否给某人贷款,这是个“分类”问题,结果只有贷和不贷两种(离散型变量);银行给某个人贷多少钱,这是个“回归”问题,因为建立的模型f(x)=w1x1+w2x2+...+wnxn+b得到的是一条直线(直线上的所有点都是连续的),给这个人贷款的额度就是这个直线上的一个点。
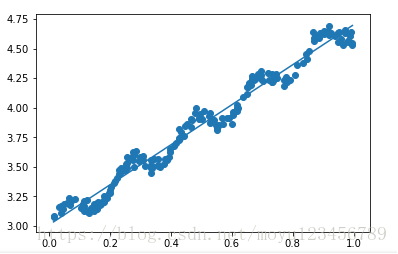
通俗来讲,线性回归就是找出一条直线,能够最大限度的拟合所有给定的特征值点(样本点)。如下图所示,其中的所有蓝色小圆点即给定的多个样本点示例,那条蓝色直线就是经过线性回归拟合所有样本点得到的预测线。这么说来,线性回归和数学里边讲的给定一条直线上的几个点(理解为样本点),要求你求出该直线方程的题是一样一样的。这里的方程式称为“回归方程”,要求的参数称为“回归参数”。
但是,通常根据样本点直接求解回归方程中的参数往往是难以求出的,此时就需要转换思路。可以这样来想,“预测值”之所以称之为“预测值”,是因为和真实值之间总是有误差存在的。那么,只要我们能将误差的最小值求出来,不就可以做到误差值和真实值之间的“无限接近”了吗?就好比张三从银行只能贷款5000块,但是银行通过预测模型预测张三能贷款5100块;李四实际能从银行贷款10000块,但是银行通过预测模型预测李四能贷款9990块。绝大多数情况下,银行可能多给,也可能少给,这样的小误差是可以接受的。
设定y为真实值,f(x)为预测值,e为误差值,则有如下公式:
y = f(x)+e
对于任意一个x(其中包括x1,x2...xn),总有其对应的y值。此时,线性回归的问题就变成了求解最小误差值的问题。
3. 误差值e最小化的求解
1)先说清楚一个概念:高斯分布。
高斯分布也称为正态分布,其概率密度函数如下:
其中, 、( >0)为常数,x的取值范围为:负无穷到正无穷。即表示x服从参数 、 的正态分布或高斯分布。正态分布的的曲线图类似于“钟形”,如下图(来源于互动百科)所示:
那么,高斯分布和线性回归的误差e有什么关系呢?
因为误差e(每个样本会产生一个ei)是独立并且具有相同的分布,并且服从均值为0方差为w2的高斯分布。-----请注意,这里是一种机器学习中的假设,实际中可能并不存在完完全全的独立和同分布。这种假设没有严密的数学逻辑来证明,但是采用该模型得出的结论却是正确的。
还是采用银行贷款的例子来进行解释:
独立的解释:任何一个来银行贷款的人之间是独立而没有关系的,这里的没有关系是指银行是否贷款给张三,这和李四没有关系。
同分布解释:任何一个人都来我们模型假定的这家银行贷款,遵守同样的规则(现实中走后门托人找关系的情况这里不考虑)。
高斯分布在此情况下的解释:对于每个贷款人,银行可能多给也可能少给,但是大多数情况下上下浮动不会太大,只有极小情况下浮动较大,这些符合正常情况。
则,此时对于误差e,代入高斯分布的公式得x的概率密度函数:
p(x) = 
又可以从y=f(x)+e推出e=y-f(x)=y-wTx,代入上式可得:
p(y|x;w) = 
2)似然函数
以下是浙大《概率论与数理统计》一书中关于似然函数的定义:
对于线性回归而言,样本值x(x1,x2,x3,...,xn)是已知的,此时需要计算在已知的样本值上取得的最大概率L()值时的值,在本文中就是计算w的值(w为权重向量)。此时的似然函数如下:
对以上似然函数简单解释为:什么样的参数w,和已知的样本数据X(x1,x2,...,xn)组合后,恰好是真实值。其实也就是似然函数取得最大值。则,问题转换为求L(w)的最大值。
观察L(w),发现是一堆数据相乘的操作,对于相乘的操作求其最大值是比较困难的。此时,将其转换为对数来求解:
又由于对数运算的性质:logA*B=logA+logB,此时该表达式可转换为如下:
此时,问题转换为让对数似然函数越大越好(对数似然函数越大==>似然函数越大)。分析以上展开后的logL(w)式子,可知



越小越好。
2)最小二乘法
由2)中可得,当前的求解对象已经转换为求
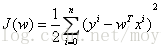
在该式中需要求解什么样的w使得J(w)最小。许多介绍线性回归的文章一上来就直接进入最小二乘法的使用,让人很摸不着头脑???这个公式是怎么推导出来的呢???本文给出了最小二乘法公式的推导过程。
对J(w)关于w求导如下:
至此,导数已经求出。J(w)取得最小值的地方一定是在其对w求偏导为0时的w处取得。
令此即我w矩阵的值。
值得注意的是,上式中包含,因此这个方程只在逆矩阵存在时适用,也就是说直接使用此公式要求必须是满秩的。实际进行线性回归求解时,往往会遇到大量的特征值,它们的个数比样本点数还多,此时X就不再是满秩矩阵了,进行求逆就会出现错误。这种情况下要进行线性回归求解,需要用到诸如岭回归、lasso法、前向逐步回归等方法。不在本文范围内介绍。
以下是运行《机器学习实战》中线性回归的相关代码示例:
from numpy import *
import matplotlib.pyplot as plt
def loadDataSet(fileName):
numFeat = len(open(fileName).readline().split('\t'))-1
dataMat = [];
labelMat = [];
fr = open(fileName)
for line in fr.readlines():
lineArr = []
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat, labelMat
def standRegres(xArr, yArr):
xMat = mat(xArr)
yMat = mat(yArr).T
xTx = xMat.T*xMat
if linalg.det(xTx) == 0.0: #判断行列式是否为0,此处就是判断是否可求逆
print("This matrix is singular, cannot do inverse")
return
ws = xTx.I*(xMat.T*yMat)
return ws
def main():
xArr, yArr = loadDataSet('ex0.txt')
print(xArr[0:2])
ws = standRegres(xArr, yArr)
print(ws)
xMat = mat(xArr)
yMat = mat(yArr)
yHat = xMat * ws
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xMat[:,1].flatten().A[0], yMat.T[:, 0].flatten().A[0])
xCopy=xMat.copy()
xCopy.sort(0)
yHat=xCopy*ws
ax.plot(xCopy[:,1], yHat)
plt.show()
if __name__ == '__main__':
main()
运行结果如下:
前文的那张展示线性回归拟合样本点的图就来自于这个例子,在这个代码示例中,是直接将前边求出的w的公式代入进行计算的。