再读线性回归 Linear Regression (逻辑回归)

1. 逻辑回归

线性回归算法旨在通过训练一定量的样本来预测 连续型数值（Continuous Value）（即回归问题）。当然了，聪明的科学家们早就想好如何将线性回归运用到 离散型数值（Discrate value） 的预测上了（即分类问题）。我们将这种运用在分类问题上的线性回归模型称之为 逻辑回归（Logistic Regression）。

简单的来说，逻辑回归仅仅是将线性回归的输出值做了一定的处理，并设置一个阈值。当预测的输出值大于或等于这个阈值时，将样本分为一类；当预测的输出与之小于这个阈值时，将样本分为另一类。一个常见的例子就是给线性回归结果上加上 Sigmoid 函数（或称 Logisitc 函数），如此一来，线性回归的输出值就固定在 0 到 1 之间了。我们设置阈值为 0.5，当预测值大于 0.5 时，认为样本为正类；反之则为负类。
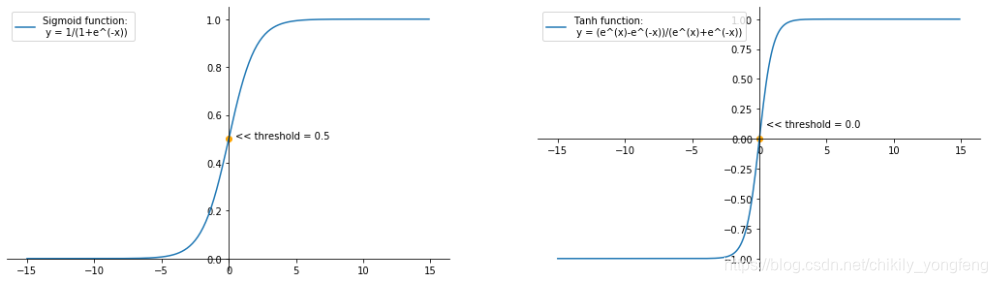
在这里插入图片描述
上图左边展示了标准的 Sigmoid 函数，它将整个 x 轴平均分为 2 部分，即 $x \geq 0$ 时样本为正，当 $x < 0$ 时样本为负，我们记这个函数为 $g(z)$ 。因此，逻辑回归的函数可以写为，

$h_{\theta}(x) = g(\theta^Tx)，其中 g(z)=\frac{1}{1+e^{z}}$

其中， $\theta$ 是 n+1 维参数向量（ $\theta \in \mathbb{R}^{(n+1)\times1}$ ）。 $x$ 表示单个样本，也是 n+1 维向量（ $x \in \mathbb{R}^{(n+1)\times1}$ ）。对于每个样本 $x$ ，我们通过计算其 $h_{\theta}(x)$ 的值来判断它到底术语正类还是负类，其预测类别为，

$类别 = \begin{cases} 1，h_{\theta}(x) \geq 0.5 \\ 0，h_{\theta}(x) < 0.5 \end{cases}$

2. 决策边界 Decision Boundary

线性回归和逻辑回归最大的不同在于预测值 $h_{\theta}(x)$ 的计算。即在线性回归中， $h_{\theta}(x)=\theta^Tx$ 。而在逻辑回归中， $h_{\theta}(x)=g(\theta^Tx)$ 。若设置分类的阈值为 0.5，那么判断 $h_{\theta}(x)$ 与 0 的关系，等价于判断 $\theta^Tx$ 与 0 的关系。换句话说，如果 $\theta^Tx$ 大于等于 0，则 $x$ 为正类样本，反之则为负类样本。因此， $\theta^Tx=0$ 构成了逻辑回归的决策边界，具体的，

$\theta^Tx = \theta_0x_0+\theta_1x_1 + ...+\theta_nx_n = 0.$

2.1 线性决策边界

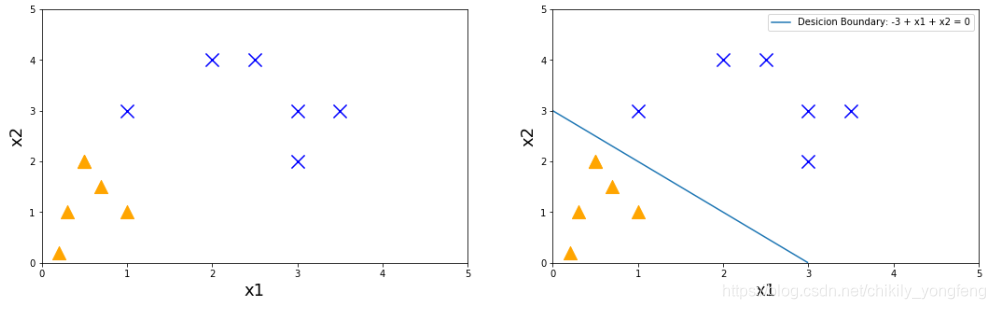
举个例子，现需要针对下图中的正类和负类样本进行分类。每个样本 $x=(x_1;x_2)$ 都是一个二维向量。现在，假设我们训练好的参数 $\theta=(-3;1;1)$ ，那么我们根据逻辑回归生成的决策边界为，

$决策边界：-3+x_1+x_2=0$

由于这个决策边界是关于 $x1,x2$ 的线性表达式，故这个决策边界也成为线性决策边界。线性决策边界是分类问题中最简单最基础的。
在这里插入图片描述

2.2 非线性决策边界

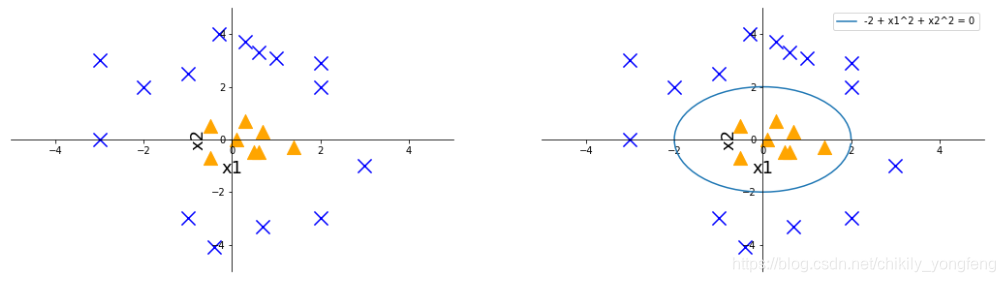
另一个例子，假设正类和负类样本的分布如下图所示，我们很难通过一条直线将它们分割开。这个时候我们需要一个非线性的决策边界。这个时候简单的 $x1,x2$ 2 项不能很好的分类，我们需要增加到 2 次方的多项式，如 $x_1^2$ 或 $x_2^2$ 。那么假设学习到的参数 $\theta=(-2;0;0;1;0;1)$ ，那么对应的决策边界为，

$决策边界：-2 + x_1^2 + x_2^2 = 0$

因此，只要将回归方程中的项的次数升高，逻辑回归还是具有很强的非线性分类能力的。

在这里插入图片描述

3. 代价函数

逻辑回归的代价函数 $J(\theta)$ 比较特别，它与线性回归的代价函数不同，它更多的是一个分段函数形式呈现。也就是说，当样本 $x^{(i)}$ 是正类（ $y^{(i)}=1$ ）或负类（ $y^{(i)}=0$ ）时，计算代价的公式是不同的。【这么做的原因是保持代价函数是凸函数，也即保持只有一个全局优点】

$x^{(i)} 的代价 = \begin{cases} -log(h_{\theta}(x^{(i)}))，y^{(i)}=1 \\ -log(1-h_{\theta}(x^{(i)}))，y^{(i)}=0 \end{cases}$

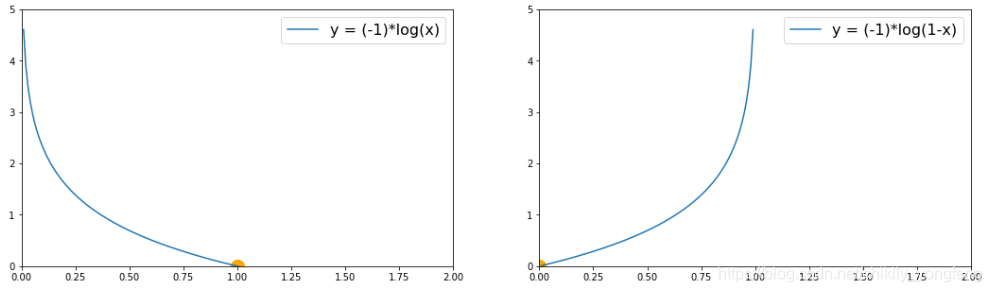
首先，当样本本来是正类时，根据 $-log(x)$ 可知：预测值越是接近 1，代价越小；当预测值越是接近 0，代价变得非常大（无穷大）。与之相反，当样本本来是负类时，根据 $-log(1-x)$ 可知：预测值越是接近 1，代价变得大（无穷大）；当预测值越是接近 0，代价越小。这个设计不得不说十分巧妙。
在这里插入图片描述
通常，为了简化代价函数（将多行写成一行的形式），我们在前面添加参数 $y$ 和 $(1-y)$ ，这样代价函数 x^{(i)} 的代价也可以写成，

$x^{(i)} 的代价 =y^{(i)}[(-1)\times log(h_{\theta}(x^{(i)}))]+(1-y^{(i)})[(-1)\times -log(1-h_{\theta}(x^{(i)}))]$

因此总的代价函数 $J(\theta)$ 可看做是所有样本 $x^{(i)}$ 的代价之和（ $m$ 表示样本个数），记为，

$J(\theta)= \frac{1}{m}\sum_{i=1}^{m} \{y^{(i)}[(-1)\times log(h_{\theta}(x^{(i)}))]+(1-y^{(i)})[(-1)\times -log(1-h_{\theta}(x^{(i)}))]\}$

4. 参数优化

在逻辑回归中，我们沿用之前介绍的梯度下降算法（Gradient Descent）。通过每次迭代中对参数的调整来实现代价函数最小化，逻辑回归同样是求解出使得代价函数最小的参数集合 $\theta$ ，

$\theta = \mathop{\arg\min}_{\theta} J(\theta)$

同样的，我们对代价函数求导，发现其梯度与线性回归的梯度一模一样，

$\frac{\partial J}{\partial \theta_j} = \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_j，j=0,2,...,n$

每一轮迭代，调整的参数也是类似，令 $\alpha$ 为学习率，则参数项 $\theta_j$ 调整过程为，

$\theta_j = \theta_j - \frac{\alpha}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}$

我们将 j 推广到一般情况，即每次对待看做是对 $\theta$ 上的矩阵操作，令 $X$ 和 $Y$ 分别表示特征集合和标签集合，我们得到每次迭代的新的 $\theta$ 应该等于（等式同样适用于线性回归），

$\theta = \theta - \frac{\alpha}{m} X^T(X\theta-Y)$

可以说，参数调优过程跟线性回归一模一样。但是注意，逻辑回归的 $h_{\theta}(x)$ 与线性回归的不同。

5. Sklearn 实现

Sklearn 同样提供了逻辑回归算法的现成品，即 sklearn.linear_model.LogisticRegression 类¹ 。实例代码如下，函数logistic_regression_example() 建立了一个逻辑回归模型的框架，函数 set_arguments() 列出了逻辑回归中比较重要的参数。

from  sklearn.linear_model import LogisticRegression

def logistic_regression_example(args, train_x, train_y):
    # fit the train_x, train_y
    clf = LogisticRegression()
    clf.set_params(**args)
    clf.fit(train_x,train_y)
	return clf
    
def set_arguments():
    args = dict()
    args['penalty']='elasticnet' # 正则化方法, {'l1','l2','elasticnet',none'}
    args['l1_ratio']=0.5 # elasticnet 正则化情况下的 L1 正则化的比例
    args['class_weight']='balanced' # 类权值, {'balanced',dict={0:0.5,1:0.5}}
    args['max_iter']=800 # 迭代次数, default=100
    args['tol']=1e-4
    args['solver'] = 'saga' # 优化算法, {‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’}
    args['random_state']=0 # 随机种子
    return args

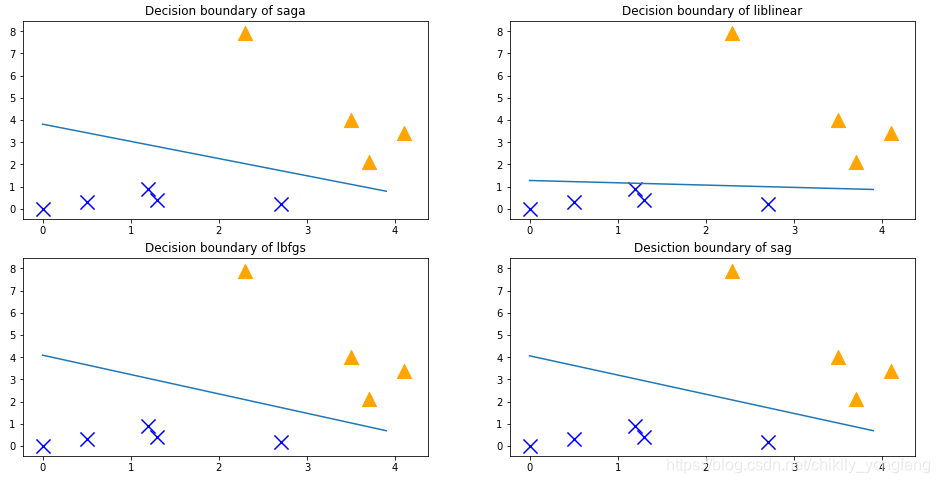
值得一提的是优化算法的参数 solver ，它对逻辑回归的预测结果影响重大。默认的选择有 ‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’（具体见博文²）。不同的优化算法对应着不同的正则化的惩罚项，即penalty 参数。‘liblinear’ 在小数据集上效果不错，此时 penalty 不能等于 ‘none’。其他的 ‘newton-cg’, ‘lbfgs’, ‘sag’ and ‘saga’ 算法，此时 penalty 必须等于 ‘l2’ 或者 ‘none’。支持 penalty=‘slasticnet’ 的只有 ‘saga’ 算法。这个在设置参数时应该留意。

另外，这个 class_weight 表示类权重，也就是说分类器分错不同类的样本的代价是不同的，这个参数可以取 ‘balanced’，也可以取一个字典，里面标记不同权重的比例，如 ‘{0:0.5,0:0.5}’。不同的权重会导致决策边界向正类或负类的方向偏移，这个参数也是处理类不平衡问题的一个好办法。

最后，不同的参数调节出来的分类效果也是不一样的，如下面 4 个子图所示。由此看来，机器学习的调参确实是很玄学。
在这里插入图片描述

LogisticRegression 官方文档. Link ↩︎
logistic 回归的sklearn实践. Link ↩︎

chikily_yongfeng

发布了14 篇原创文章 · 获赞 29 · 访问量 4万+

私信关注