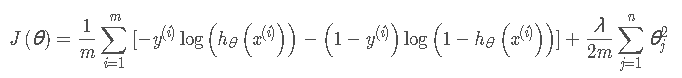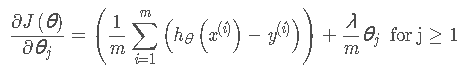Python机器学习笔记-2（logistics regression公式推导和代码实现）

1. 引言

logistic回归是机器学习中最常用最经典的分类方法之一，有人称之为逻辑回归或者逻辑斯蒂回归。虽然他称为回归模型，但是却处理的是分类问题，这主要是因为它的本质是一个线性模型加上一个映射函数Sigmoid，将线性模型得到的连续结果映射到离散型上。它常用于二分类问题，在多分类问题的推广叫softmax。

本文首先阐述Logistic回归的定义，然后介绍一些最优化算法，其中包括基本的梯度上升法和一个改进的随机梯度上升法。
在我们的日常生活中遇到过很多最优化问题，比如如何在最短时间内从A点到达B点？如何投入最少工作量却获得最大的效益？如何设计发动机使得油耗最少而功率最大？可见，最优化的作用十分强大，所以此处我们介绍几个最优化算法，并利用它们训练出一个非线性函数用于分类。

现在假设有一些数据点，我们用一条直线对这些点进行拟合（该线称为最佳拟合直线），这个拟合过程就称作回归。利用logistic回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类，这里的“回归”一词源于最佳拟合，表示要找到最佳拟合参数集。训练分类器时的做法就是寻找最佳拟合参数，使用的是最优化算法，下面我们首先介绍一下这个二值型输出分类器的数学原理。

2. Logistic回归的一般过程

1. 收集数据：采用任意方法收集数据

2. 准备数据：由于需要进行距离计算，因此要求数据类型为数值型。另外，结构化数据格式则最佳

3. 分析数据：采用任意方法对数据进行分析

4. 训练算法：大部分时间将用于训练，训练的目的是为了找到最佳的分类回归系数

5. 使用算法：首先，需要输入一些数据，并将其转换成对应的结构化数值；接着，基于训练好的回归系数就可以对这些数值进行简单的回归计算，判定他们属于哪个类别；在这之后，我们就可以在输出的类别上做一些其他分析工作。

3. Logistic回归的优缺点

优点：计算代码不多，易于理解和实现，计算代价不高，速度快，存储资源低

缺点：容易欠拟合，分类精度可能不高

适用数据类型：数值型和标称型数据

4. 基于Logistic回归和Sigmoid函数的分类

我们想要的函数应该是，能接受所有的输入，然后预测出类型。例如，在两个类的情况下，上述函数输出0或1。该函数称为海维赛德阶跃函数（Heaviside step function），或者直接称为单位阶跃函数。然而，海维赛德阶跃函数的问题在于：该函数在跳跃点上从0瞬间跳跃到1，这个瞬间跳跃过程有时很难处理。幸好，另一个函数也有类似的性质（可以输出0或者1），且数学上更易处理，这就是Sigmoid函数。Sigmoid函数具体的计算公式为： $sigmoid=\frac{1}{1+e^{-x}}$

下面给出了Sigmoid函数在不同坐标尺度下的两条曲线图。当x为0时，Sigmoid函数值为0.5。随着x的增大，对应的Sigmoid值将逼近于1；而随着x的减少，Sigmoid值将逼近于0.如果横坐标刻度足够大，Sigmoid函数看起来很像一个阶跃函数。

因此，为了实现Logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和带入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5即被归入0类，所以，Logistic回归也可以被看成是一种概率估计。

确定了分类器的函数形式之后，现在的问题变成了：最佳回归系数是多少？如何确定其大小。
　　

5. 基于最优化方法的最佳回归系数确定

Sigmoid函数的输入记为z，由下面公式得到：
$z=w_0x_0+w_1x_1+\dots+w_nx_x$

如果采用向量的写法，上述公式可以写成 $z=w^Tx$ ，它表示将这两个数值向量对应元素相乘，然后全部加起来即得到z值。

其中的向量 $x$是分类器的输入数据，向量w也就是我们要找到的最佳参数（系数），从而使得分类器尽可能的准确，为了寻找该最佳参数，需要用到最优化理论的一些知识。

Logistic回归模型的公式：

$Y = \frac{1}{1+e^{-W^Tx}}$

这里假设 W>0，Y与X各维度叠加的图形关系，如下图所示（x为了方便取1维）：

下面首先学习梯度上升的最优化方法，我们将学习到如何使用该方法求得数据集的最佳参数，接下来，展示如何绘制梯度上升法产生的决策边界图，该图将梯度上升法的分类效果可视化的呈现出来，最后我们将学习随机梯度上升算法，以及如何对其进行修改以获得很好地结果。

注释1：梯度下降算法与这里的梯度上升算法是一样的，只是公式中的加法需要变成减法，梯度上升算法用来求函数的最大值，而梯度下降算法是用来求函数的最小值

6. 梯度上升法

梯度上升法基于的思想是：要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻，如果梯度记为 $\nabla$，则函数 f(x,y) 的梯度由下面式子表示：

这个梯度意味着要沿着x的方向移动 $\frac{\partial f(x,y)}{\partial x}$，沿着y方向移动 $\frac{\partial f(x,y)}{\partial y}$，其中函数f(x,y)必须要在待计算的点上有定义并且可微，一个具体的函数例子见下图：

上图中的梯度上升算法沿梯度方向移动了一步，可以看出，梯度算子总是指向函数值增长最快的方向。这里所说的移动方向，而未提到移动量的大小。该量值称为步长，记为 $\alpha$，用向量来表示的话，梯度算法的迭代公式如下：.

$w:=w+\alpha\nabla_wf(w)$

该公式将一直被迭代执行，直至达到某个停止条件为止，比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围。

基于上面的内容，我们来看一个Logistic回归分类器的应用例子，从图5-3可以看到我们采用的数据集。

梯度上升法的公式推导（LR 损失函数）
在LR中，应用极大似然估计法估计模型参数，由于Sigmoid函数的特性，我们可以做如下的假设：

上式即为在已知样本X和参数θ的情况下。样本X属性正类（y=1）和负类（y=0）的条件概率，将两个公式合并成一个，如下：
假定样本与样本之间相互独立，那么整个样本集生成的概率即为所有样本生成概率的乘积（也就是n个独立样本出现的似然函数如下）：

为了简化问题，我们对整个表达式求对数（即为LR 损失函数）：

满足似然函数（θ）的最大的θ值即时我们需要求解的模型。

那么梯度上升法就像爬坡一样，一点一点逼近极值，而上升这个动作用数学公式表达即为：

其中，α 为步长。

回到Logistic回归问题，我们同样对函数求偏导。

对这个公式进行分解，先看：

我们可以看到，对函数求偏导，分解为三部分，然后我们对这三部分分布求导。

第一部分：

其中(似然函数对sigmoid函数求导)：
再由(sigmoid函数求导)：

可得：

第二部分：

第三部分：

综合三部分即得到：

因此梯度迭代公式为：

7. 训练算法：使用梯度上升找到最佳参数

图有100个样本点，每个点包含两个数值型特征： $x1$和 $x2$，在此数据集上，我们将通过使用梯度上升法找到最佳回归系数，也就是拟合出Logistic回归模型的最佳参数。
梯度上升法的伪代码如下：

每个回归系数初始化为1
重复R次：
	计算整个数据集的梯度
    使用alpha * gradient 更新回归系数的向量
    返回回归系数

数据testSet.txt：

-0.017612   14.053064   0
-1.395634   4.662541    1
-0.752157   6.538620    0
-1.322371   7.152853    0
0.423363    11.054677   0
0.406704    7.067335    1
0.667394    12.741452   0
-2.460150   6.866805    1
0.569411    9.548755    0
-0.026632   10.427743   0
0.850433    6.920334    1
1.347183    13.175500   0
1.176813    3.167020    1
-1.781871   9.097953    0
-0.566606   5.749003    1
0.931635    1.589505    1
-0.024205   6.151823    1
-0.036453   2.690988    1
-0.196949   0.444165    1
1.014459    5.754399    1
1.985298    3.230619    1
-1.693453   -0.557540   1
-0.576525   11.778922   0
-0.346811   -1.678730   1
-2.124484   2.672471    1
1.217916    9.597015    0
-0.733928   9.098687    0
-3.642001   -1.618087   1
0.315985    3.523953    1
1.416614    9.619232    0
-0.386323   3.989286    1
0.556921    8.294984    1
1.224863    11.587360   0
-1.347803   -2.406051   1
1.196604    4.951851    1
0.275221    9.543647    0
0.470575    9.332488    0
-1.889567   9.542662    0
-1.527893   12.150579   0
-1.185247   11.309318   0
-0.445678   3.297303    1
1.042222    6.105155    1
-0.618787   10.320986   0
1.152083    0.548467    1
0.828534    2.676045    1
-1.237728   10.549033   0
-0.683565   -2.166125   1
0.229456    5.921938    1
-0.959885   11.555336   0
0.492911    10.993324   0
0.184992    8.721488    0
-0.355715   10.325976   0
-0.397822   8.058397    0
0.824839    13.730343   0
1.507278    5.027866    1
0.099671    6.835839    1
-0.344008   10.717485   0
1.785928    7.718645    1
-0.918801   11.560217   0
-0.364009   4.747300    1
-0.841722   4.119083    1
0.490426    1.960539    1
-0.007194   9.075792    0
0.356107    12.447863   0
0.342578    12.281162   0
-0.810823   -1.466018   1
2.530777    6.476801    1
1.296683    11.607559   0
0.475487    12.040035   0
-0.783277   11.009725   0
0.074798    11.023650   0
-1.337472   0.468339    1
-0.102781   13.763651   0
-0.147324   2.874846    1
0.518389    9.887035    0
1.015399    7.571882    0
-1.658086   -0.027255   1
1.319944    2.171228    1
2.056216    5.019981    1
-0.851633   4.375691    1
-1.510047   6.061992    0
-1.076637   -3.181888   1
1.821096    10.283990   0
3.010150    8.401766    1
-1.099458   1.688274    1
-0.834872   -1.733869   1
-0.846637   3.849075    1
1.400102    12.628781   0
1.752842    5.468166    1
0.078557    0.059736    1
0.089392    -0.715300   1
1.825662    12.693808   0
0.197445    9.744638    0
0.126117    0.922311    1
-0.679797   1.220530    1
0.677983    2.556666    1
0.761349    10.693862   0
-2.168791   0.143632    1
1.388610    9.341997    0
0.317029    14.739025   0

下面具体实现梯度上升算法的代码：

#_*_coding:utf-8_*_
import numpy as np
 
# 读取数据
def loadDataSet(filename):
    '''
        对于testSet.txt，每行前两个值分别是X1和X2，第三个值数据对应的类别标签
        而且为了设置方便，该函数还将X0的值设置为1.0
        :return:
        '''
    dataMat = []
    labelMat = []
    fr = open(filename)
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat
 
def sigmoid(inX):
    return 1.0/(1+np.exp(-inX))
 
def gradAscent(dataMatIn,classLabels):
    '''
        param dataMatIn: 是一个2维Numpy数组，每列分别代表每个不同的特征
        每行则代表每个训练样本。
        param classLabels: 是类别标签，是一个1*100的行向量，为了便于矩阵运算，需要将行向量
        转换为列向量，就是矩阵的转置，再将其赋值与labelMat。
        :return:
        '''
    dataMatrix = np.mat(dataMatIn)
    labelMat = np.mat(classLabels).transpose()
    # labelMat = mat(classLabels).T
    m,n = np.shape(dataMatrix)
    # alpha是向目标移动的步长
    alpha = 0.001
    # 迭代次数
    maxCycles = 500
    weights = np.ones((n,1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)
        error = (labelMat-h)
        weights = weights + alpha*dataMatrix.transpose()*error
    return weights

测试结果如下：

if __name__  == '__main__':
    filename = 'testSet.txt'
    dataArr,labelMat = loadDataSet(filename)
    weights_res = gradAscent(dataArr,labelMat)
    print(weights_res)
     
'''
[[ 4.12414349]
 [ 0.48007329]
 [-0.6168482 ]]
 '''

上面已经解出了一组回归系数，它确定了不同类别数据之间的分割线，那么怎样画出该分割线，从而使得优化的过程便于理解呢？下面代码来解决这个问题。

画出数据集和Logistic回归最佳拟合直线的函数代码：

def plotBestFit(wei):
    import matplotlib.pyplot as plt
    weights = wei.getA()
    dataMat,labelMat = loadDataSet(filename)
    dataArr = array(dataMat)
    n = shape(dataArr)[0]
    xcord1 = []
    ycord1 = []
    xcord2 = []
    ycord2 = []
    for i in range(n):
        if int(labelMat[i]) ==1:
            xcord1.append(dataArr[i,1])
            ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i, 1])
            ycord2.append(dataArr[i, 2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')
    ax.scatter(xcord2,ycord2,s=30,c='green')
    x = arange(-3.0,3.0,0.1)
    y = (-weights[0]-weights[1] * x) / weights[2]
    ax.plot(x,y)
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.show()

输出的结果和代码如下图所示：

if __name__  == '__main__':
    filename = 'testSet.txt'
    dataArr,labelMat = loadDataSet(filename)
    weights_res = gradAscent(dataArr,labelMat)
    print(weights_res)
    plotBestFit(weights_res)

梯度上升算法在500次迭代后得到的Logistic回归最佳拟合直线:
这个分类结果相当不错，从图上看，只错分了四个点。但是，尽管例子简单且数据集很小，这个方法却需要大量的计算（300次乘法），因此下一节将对算法稍作改进，从而使它可以用在真实数据集上。

8. 训练算法：随机梯度上升

梯度上升算法在每次更新回归系数时都需遍历整个数据集，该方法在处理100个左右的数据集尚可，但是若有数十亿样本和成千上万的特征，那么该方法的计算复杂度就太高了。一种改进方法是一次仅用一个样本点来更新回归系数，该方法称为随机梯度上升算法。由于可以在新样本到来时对分类器进行增量式更新，因而随机梯度上升算法是一个在线学习算法，与“在线学习”相对应，一次处理所有数据被称作是“批处理”。

随机梯度上升算法可以写成如下的伪代码：

所有回归系数初始化为1
对数据集中每个样本
    计算该样本的梯度
    使用alpha*gradient 更新回归系数值
返回回归系数值

以下是随机梯度上升算法的实现代码：

def stocGradAscent0(dataMatrix,classLabels):
    m,n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        error = classLabels[i] - h
        weights = weights + alpha*error*dataMatrix[i]
    return weights

测试代码如下：

if __name__  == '__main__':
    filename = 'testSet.txt'
    dataArr,labelMat = loadDataSet(filename)
    weights_res = stocGradAscent0(array(dataArr),labelMat)
    print(weights_res)
    plotBestFit(weights_res)

随机梯度上升算法在上述数据集上的执行结果，最佳拟合直线并非最佳分类线

改进的随机梯度上升算法代码如下：

# 改进的随机梯度上升算法
def stocGradAscent1(dataMatrix,classLabels,numIter=150):
    m,n = shape(dataMatrix)
    weights = ones(n)
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01
            randIndex = int(random.uniform(0,len(dataIndex)))
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha *error*dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

上述代码大体上与之前的随机梯度上升算法一致，修改了两处，一处是alpha在每次迭代的时候都会调整，这会环节之前的数据波动或者高频波动。另外，虽然alpha会随着迭代次数不断减少，但永远不会减少到0。必须这样做的原因是为了保证在多次迭代之后新数据仍然具有一定的影响。如果要处理的问题是动态变化的，那么可以适当增加常数项，来确保新的值获得更大的回归系数。另外一点值得注意的是，在降低alpha的函数中，alpha每次减少1/(j+1)，其中j是迭代次数，i是样本点的下标，这样当j<max(i)的时候，alpha就不是严格下降的，避免参数的严格下降也常见于模拟退火算法等其他优化算法中。程序的第二个改进地方就是通过随机选取样本来更新回归系数，这种方法将减少周期性的波动，并且改进的算法还增加一个迭代次数作为第三个参数，如果该参数没有给定的话，算法将默认迭代150次，如果给定，那么算法将按照新的参数值进行迭代。

下面看看在同一个数据集上的分类效果，将程序运行可以看到：

if __name__  == '__main__':
    filename = 'testSet.txt'
    dataArr,labelMat = loadDataSet(filename)
    weights_res = stocGradAscent1(array(dataArr),labelMat)
    print(weights_res)
    plotBestFit(weights_res)

该分割线达到了与GradientAscent()差不多的效果，但是所使用的计算量更少。

默认的迭代次数是150次，但是我们通过stocGradAscent()的第三个参数来对此进行修改，例如：

weights_res = stocGradAscent1(array(dataArr),labelMat,500)

9. 总结

Logistic回归的目的是寻找一个非线性函数Sigmoid的最佳拟合参数，求解过程可以由最优化算法来完成。在最优化算法中，最常用的就是梯度上升算法，而梯度上升算法又可以简化为随机梯度上升算法。

随机梯度上升算法与梯度上升算法的效果相当，但是占用更少的计算资源。此外，随机梯度上升是一个在线算法，它可以在新数据到来时就完成参数更新，不需要重新读取整个数据集来进行批处理运算。

机器学习的一个重要问题就是如何处理缺失数据，这个问题没有标准答案，取决于实际应用中的需求。

10. 推广

Logistic回归模型主要用于二分类，多分类问题中的推广——softmax回归。

softmax与Logistic回归的主要区别就是，Logistic处理二分类问题，只有一组权重参数θ，而softmax处理多分类问题，如果有k个类别，那么softmax就有k组权值参数。每组权值对应一种分类，通过k组权值求解出样本数据对应每个类别的概率，最后取概率最大的类别作为该数据的分类结果，它的概率函数为：

softmax函数经常用于神经网络的最后一层，用于对神经网络已经处理好的特征进行分类。

基于Sklearn构建Logistic回归分类器

LogisticRegression

LogisticRegression这个函数，一共有14个参数

参数说明如下：

penalty：惩罚项，str类型，可选参数为l1和l2，默认为l2。用于指定惩罚项中使用的规范。newton-cg、sag和lbfgs求解算法只支持L2规范。L1G规范假设的是模型的参数满足拉普拉斯分布，L2假设的模型参数满足高斯分布，所谓的范式就是加上对参数的约束，使得模型更不会过拟合(overfit)，但是如果要说是不是加了约束就会好，这个没有人能回答，只能说，加约束的情况下，理论上应该可以获得泛化能力更强的结果。
　　dual：对偶或原始方法，bool类型，默认为False。对偶方法只用在求解线性多核(liblinear)的L2惩罚项上。当样本数量>样本特征的时候，dual通常设置为False。
　　tol：停止求解的标准，float类型，默认为1e-4。就是求解到多少的时候，停止，认为已经求出最优解。
　　c：正则化系数λ的倒数，float类型，默认为1.0。必须是正浮点型数。像SVM一样，越小的数值表示越强的正则化。
　　fit_intercept：是否存在截距或偏差，bool类型，默认为True。如果使用中心化的数据，可以考虑设置为False,不考虑截距。注意这里是考虑，一般还是要考虑截距
　　intercept_scaling：仅在正则化项为”liblinear”，且fit_intercept设置为True时有用。float类型，默认为1。
　　class_weight：用于标示分类模型中各种类型的权重，可以是一个字典或者balanced字符串，默认为不输入，也就是不考虑权重，即为None。如果选择输入的话，可以选择balanced让类库自己计算类型权重，或者自己输入各个类型的权重。举个例子，比如对于0,1的二元模型，我们可以定义class_weight={0:0.9,1:0.1}，这样类型0的权重为90%，而类型1的权重为10%。如果class_weight选择balanced，那么类库会根据训练样本量来计算权重。某种类型样本量越多，则权重越低，样本量越少，则权重越高。当class_weight为balanced时，类权重计算方法如下：n_samples / (n_classes * np.bincount(y))。n_samples为样本数，n_classes为类别数量，np.bincount(y)会输出每个类的样本数，例如y=[1,0,0,1,1],则np.bincount(y)=[2,3]。
　　　　那么class_weight有什么作用呢？ 在分类模型中，我们经常会遇到两类问题：

1，第一种是误分类的代价很高。比如对合法用户和非法用户进行分类，将非法用户分类为合法用户的代价很高，我们宁愿将合法用户分类为非法用户，这时可以人工再甄别，但是却不愿将非法用户分类为合法用户。这时，我们可以适当提高非法用户的权重。
2，第二种是样本是高度失衡的，比如我们有合法用户和非法用户的二元样本数据10000条，里面合法用户有9995条，非法用户只有5条，如果我们不考虑权重，则我们可以将所有的测试集都预测为合法用户，这样预测准确率理论上有99.95%，但是却没有任何意义。这时，我们可以选择balanced，让类库自动提高非法用户样本的权重。提高了某种分类的权重，相比不考虑权重，会有更多的样本分类划分到高权重的类别，从而可以解决上面两类问题。
　　random_state：随机数种子，int类型，可选参数，默认为无，仅在正则化优化算法为sag,liblinear时有用。
　　solver：优化算法选择参数，只有五个可选参数，即newton-cg,lbfgs,liblinear,sag,saga。默认为liblinear。solver参数决定了我们对逻辑回归损失函数的优化方法，有四种算法可以选择，分别是：

liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。
lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
newton-cg：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
sag：即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。
saga：线性收敛的随机优化算法的的变重。
总结：

liblinear适用于小数据集，而sag和saga适用于大数据集因为速度更快。
对于多分类问题，只有newton-cg,sag,saga和lbfgs能够处理多项损失，而liblinear受限于一对剩余(OvR)。啥意思，就是用liblinear的时候，如果是多分类问题，得先把一种类别作为一个类别，剩余的所有类别作为另外一个类别。一次类推，遍历所有类别，进行分类。
newton-cg,sag和lbfgs这三种优化算法时都需要损失函数的一阶或者二阶连续导数，因此不能用于没有连续导数的L1正则化，只能用于L2正则化。而liblinear和saga通吃L1正则化和L2正则化。
同时，sag每次仅仅使用了部分样本进行梯度迭代，所以当样本量少的时候不要选择它，而如果样本量非常大，比如大于10万，sag是第一选择。但是sag不能用于L1正则化，所以当你有大量的样本，又需要L1正则化的话就要自己做取舍了。要么通过对样本采样来降低样本量，要么回到L2正则化。
从上面的描述，大家可能觉得，既然newton-cg, lbfgs和sag这么多限制，如果不是大样本，我们选择liblinear不就行了嘛！错，因为liblinear也有自己的弱点！我们知道，逻辑回归有二元逻辑回归和多元逻辑回归。对于多元逻辑回归常见的有one-vs-rest(OvR)和many-vs-many(MvM)两种。而MvM一般比OvR分类相对准确一些。郁闷的是liblinear只支持OvR，不支持MvM，这样如果我们需要相对精确的多元逻辑回归时，就不能选择liblinear了。也意味着如果我们需要相对精确的多元逻辑回归不能使用L1正则化了。
　　max_iter：算法收敛最大迭代次数，int类型，默认为10。仅在正则化优化算法为newton-cg, sag和lbfgs才有用，算法收敛的最大迭代次数。
　　multi_class：分类方式选择参数，str类型，可选参数为ovr和multinomial，默认为ovr。ovr即前面提到的one-vs-rest(OvR)，而multinomial即前面提到的many-vs-many(MvM)。如果是二元逻辑回归，ovr和multinomial并没有任何区别，区别主要在多元逻辑回归上。

OvR和MvM有什么不同？
OvR的思想很简单，无论你是多少元逻辑回归，我们都可以看做二元逻辑回归。具体做法是，对于第K类的分类决策，我们把所有第K类的样本作为正例，除了第K类样本以外的所有样本都作为负例，然后在上面做二元逻辑回归，得到第K类的分类模型。其他类的分类模型获得以此类推。
而MvM则相对复杂，这里举MvM的特例one-vs-one(OvO)作讲解。如果模型有T类，我们每次在所有的T类样本里面选择两类样本出来，不妨记为T1类和T2类，把所有的输出为T1和T2的样本放在一起，把T1作为正例，T2作为负例，进行二元逻辑回归，得到模型参数。我们一共需要T(T-1)/2次分类。
可以看出OvR相对简单，但分类效果相对略差（这里指大多数样本分布情况，某些样本分布下OvR可能更好）。而MvM分类相对精确，但是分类速度没有OvR快。如果选择了ovr，则4种损失函数的优化方法liblinear，newton-cg,lbfgs和sag都可以选择。但是如果选择了multinomial,则只能选择newton-cg, lbfgs和sag了。
　　verbose：日志冗长度，int类型。默认为0。就是不输出训练过程，1的时候偶尔输出结果，大于1，对于每个子模型都输出。
　　warm_start：热启动参数，bool类型。默认为False。如果为True，则下一次训练是以追加树的形式进行（重新使用上一次的调用作为初始化）。
　　n_jobs：并行数。int类型，默认为1。1的时候，用CPU的一个内核运行程序，2的时候，用CPU的2个内核运行程序。为-1的时候，用所有CPU的内核运行程序。

除此之外，LogisticRegression也有一些方法供我们使用：

有一些方法和MultinomialNB的方法都是类似的

1、sklearn利用LR模型进行三分类的原理及其代码

首先，LR将线性模型利用Sigmoid函数进一步做了非线性映射。将分类超平面两侧的正负样本点通过压缩函数转化成了以 0.5 为分类的两类：类别0 和类别1。

LR进行三分类（多分类）时，是特征的线性组合和Sigmoid函数复合的函数进行概率计算和分类的。

from IPython.display import Image
 
# Added version check for recent scikit-learn 0.18 checks
from distutils.version import LooseVersion as Version
from sklearn import __version__ as sklearn_version
 
from sklearn import datasets
import numpy as np
 
iris = datasets.load_iris()
# http://scikit-learn.org/stable/auto_examples/datasets/plot_iris_dataset.html
X = iris.data[:, [2, 3]]
print(X.shape)
y = iris.target  # 取species列，类别
 
if Version(sklearn_version) < '0.18':
    from sklearn.cross_validation import train_test_split
else:
    from sklearn.model_selection import train_test_split
 
# train_test_split方法分割数据集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=0)
 
from sklearn.preprocessing import StandardScaler
 
sc = StandardScaler()  # 初始化一个对象sc去对数据集作变换
sc.fit(X_train)  # 用对象去拟合数据集X_train，并且存下来拟合参数
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
 
from sklearn.linear_model import LogisticRegression
 
 
def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))
 
 
lr = LogisticRegression(C=1000.0, random_state=0)
# http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression
lr.fit(X_train_std, y_train)
 
# 计算该预测实例点属于各类的概率
lr.predict_proba(X_test_std[0, :].reshape(1, -1))
# Output:array([[  2.05743774e-11,   6.31620264e-02,   9.36837974e-01]])
 
# 验证predict_proba的作用
c = lr.predict_proba(X_test_std[0, :].reshape(1, -1))
# c[0, 0] + c[0, 1] + c[0, 2]
# Output:0.99999999999999989
 
# 查看lr模型的特征系数
lr = LogisticRegression(C=1000.0, random_state=0)
# http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression
lr.fit(X_train_std, y_train)
print(lr.coef_)
# Output:[[-7.34015187 -6.64685581]
#        [ 2.54373335 -2.3421979 ]
#        [ 9.46617627  6.44380858]]
 
# 验证predict_proba工作原理
Zz = np.dot(lr.coef_, X_test_std[0, :].T) + lr.intercept_
np.array(sigmoid(Zz)) / sum(np.array(sigmoid(Zz)))
# Output:array([  2.05743774e-11,   6.31620264e-02,   9.36837974e-01])
# 此结果就是预测实例点各类的概率

2、使用Sklearn的Logistic回归算法计算鸢尾花：

from sklearn import datasets
from numpy import *
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
 
 
def colicSklearn():
    iris = datasets.load_iris()
    X = iris.data
    Y = iris.target
    trainingSet,testSet,trainingLabels,testLabels = train_test_split(X,Y,test_size=0.25,random_state=40)
    classifier = LogisticRegression(solver='sag', max_iter=5000).fit(trainingSet, trainingLabels)
    test_accurcy = classifier.score(testSet, testLabels) * 100
    print("正确率为%s%%" % test_accurcy)
 
if __name__  == '__main__':
    colicSklearn()

使用Sklearn的Logistic回归算法预测线性回归函数：

#_*_coding:utf-8_*_
'''
下面这个例子，从数据产生，到数据提取，数据标准化
模型训练和评估来说明各个API的调用过程
'''
print(__doc__)
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# import matplotlib as mpl
import pylab as mpl
 
# 设置字符集，防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
 
# 定义目标函数通过改函数产生对应的y
# y = 1 *x[0] + 2 *x[1] + ... (n+1) *x[n]
def l_model(x):
    params = np.arange(1, x.shape[-1] +1)
    y = np.sum(params *x) + np.random.randn(1) * 0.1
    return y
 
# 定义数据集
x = pd.DataFrame(np.random.rand(500,6))
# print(x)
y = x.apply(lambda x_rows:pd.Series(l_model(x_rows)),axis=1)
# print(y)
 
# 划分数据集
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.3,random_state=2)
 
# 数据标准化
ss = StandardScaler()
x_train_s = ss.fit_transform(x_train)
x_test_s = ss.fit_transform(x_test)
 
# 输出下元数据的标准差和平均数
print(ss.scale_)
print(ss.mean_)
 
# 训练模型
lr = LinearRegression()
lr.fit(x_train_s , y_train)
# 训练后的输入端模型系数，如果label有两个，即y值有两列，那么是一个2D的array
print(lr.coef_)
# 截距
print(lr.intercept_)
 
# 用模型预测,并计算得分
y_predict = lr.predict(x_test_s)
test_accuracy = lr.score(x_test_s, y_test)
 
print("正确率为%s%%" % test_accuracy)
 
# 预测值和实际值画图比较
t = np.arange(len(x_test_s))
# 建一个画布，facecolor是背景色
plt.figure(facecolor='W')
plt.plot(t, y_test, 'r-', linewidth= 2, label = '真实值')
plt.plot(t, y_predict, 'b-', linewidth= 1, label = '预测值')
# 显示图例，设置图例的位置
plt.legend(loc= 'upper left')
plt.title("线性回归预测真实值之间的关系", fontsize = 20)
# 加网格
plt.grid(b = True)
plt.show()

正则化逻辑回归

要通过加入正则项提升逻辑回归算法。正则化有助于减少过拟合，提高模型的泛化能力。
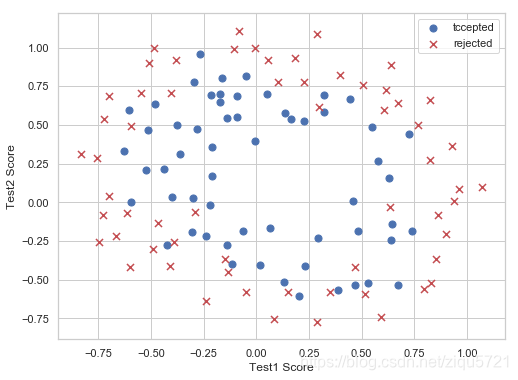
设想你是工厂的生产主管，你有一些芯片在两次测试中的测试结果。对于这两次测试，你想决定是否芯片要被接受或抛弃。为了帮助你做出艰难的决定，你拥有过去芯片的测试数据集，从其中你可以构建一个逻辑回归模型。

data2 = pd.read_csv('ex2data2.txt',header=None,names = ['test1','test2','accepted'])

positive = data2[data2['accepted'].isin([1])]
negative = data2[data2['accepted'].isin([0])]

fig, ax = plt.subplots(figsize=(8,6))
ax.scatter(positive['test1'], positive['test2'], s=50, c='b', marker='o', label='tccepted')
ax.scatter(negative['test1'], negative['test2'], s=50, c='r', marker='x', label='rejected')
ax.legend()
ax.set_xlabel('Test1 Score')
ax.set_ylabel('Test2 Score')

feature mapping（特征映射）

这个数据看起来可比前一次的复杂得多。特别地，你会注意到其中没有线性决策界限，来良好的分开两类数据。一个方法是用像逻辑回归这样的线性技术来构造从原始特征的多项式中得到的特征。

for i in 0..i
  for p in 0..i:
    output x^(i-p) * y^p

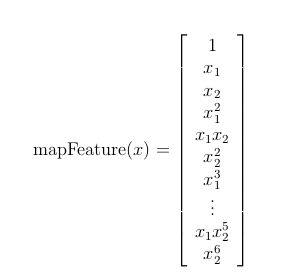
def feature_mapping(x, y, power, as_ndarray=False):

    data = {"f{}{}".format(i - p, p): np.power(x, i - p) * np.power(y, p)
                for i in np.arange(power + 1)
                for p in np.arange(i + 1)
            }

    if as_ndarray:
        return pd.DataFrame(data).as_matrix()
    else:
        return pd.DataFrame(data)
        
x1 = np.array(data2.test1)
x2 = np.array(data2.test2)

d = feature_mapping(x1, x2, power=6)
print(d.shape)

# set X and y (remember from above that we moved the label to column 0)
cols = d.shape[1]
X2 = d.iloc[:,0:cols]
y2 = data2.iloc[:,-1]

# convert to numpy arrays and initalize the parameter array theta
X2 = np.array(X2.values)
y2 = np.array(y2.values)
theta2 = np.zeros(d.shape[1])
X2.shape

regularized cost（正则化代价函数）

def regularized_cost(theta, X, y, l = 1):
    theta_j1_to_n = theta[1:]
    regularized_term = (l / (2 * len(X))) * np.power(theta_j1_to_n, 2).sum() # 注意theta_j0为偏置项，一般不参加到正则项的正则过程中
    return cost(theta, X, y) + regularized_term
#正则化代价函数

regularized_cost(theta2, X2, y2)
81.79136730607354

注意等式中的"reg" 项。还注意到另外的一个“学习率”参数。这是一种超参数，用来控制正则化项。现在我们需要添加正则化梯度函数：

regularized gradient(正则化梯度)

def gradientReg(theta, X, y, l = 1):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    
    error = sigmoid(X * theta.T) - y
    
    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        
        if (i == 0):
            grad[i] = np.sum(term) / len(X)
        else:
            grad[i] = (np.sum(term) / len(X)) + ((l/ len(X)) * theta[:,i])
    
    return grad

gradientReg(theta2,X2,y2,l)

array([ 1.00000000e+00,  5.47789085e-02,  1.83101559e-01,  2.47575335e-01,
       -2.54718403e-02,  3.01369613e-01,  5.98333290e-02,  3.06815335e-02,
        1.54825117e-02,  1.42350013e-01,  1.22538429e-01, -5.25103811e-03,
        5.04328744e-02, -1.10481882e-02,  1.71098505e-01,  5.19650721e-02,
        1.18117999e-02,  9.43209446e-03,  1.82778085e-02,  4.08908411e-03,
        1.15709633e-01,  7.83711827e-02, -7.02782670e-04,  1.89334033e-02,
       -1.70495724e-03,  2.25916984e-02, -6.30180777e-03,  1.25725602e-01])

使用 scipy.optimize.minimize 去拟合参数

import scipy.optimize as opt
#print('init cost = {}'.format(regularized_cost(theta, X2, y2)))

res = opt.minimize(fun=regularized_cost, x0=theta2, args=(X2, y2), method='Newton-CG', jac=gradientReg)
res

     fun: 81.77441734193648
     jac: array([ 4.00721538e-05,  7.92107259e-06, -9.57130728e-06, -1.42508119e-05,
        4.85128609e-07,  1.45625425e-05,  3.29183446e-06, -8.83742842e-06,
       -1.54701906e-05,  6.29085218e-06,  3.15309983e-07, -1.77766493e-06,
       -1.69611923e-06,  4.61593901e-07,  2.27856315e-05,  9.39896102e-07,
       -6.13323667e-06, -5.07992963e-06,  4.76323762e-07, -1.47010548e-06,
        8.05396260e-06, -1.23147530e-06, -2.44197649e-06, -5.84739722e-07,
       -5.07920552e-07,  2.30737982e-07,  3.82757197e-06,  1.74447504e-05])
 message: "Warning: CG iterations didn't converge.  The Hessian is not positive definite."
    nfev: 7
    nhev: 0
     nit: 6
    njev: 1303
  status: 3
 success: False
       x: array([-3.39005803e-02,  1.10730363e-06,  9.39802365e-07, -6.09094336e-06,
        1.10972567e-06, -3.46309190e-06, -5.07574755e-06, -6.50187565e-06,
       -1.85556215e-06,  3.83480279e-06,  1.19556899e-05, -2.56049482e-06,
        1.03818042e-05,  7.10689627e-07, -1.07740558e-06,  6.38125479e-06,
        9.62469243e-06, -1.14576956e-06, -2.41930553e-06,  2.82923184e-06,
       -1.06295485e-05, -9.43499460e-06, -4.88500460e-07, -2.65549579e-06,
        4.89514367e-06, -5.46760048e-07, -4.56236184e-06,  9.44055863e-06])

final_theta =np.matrix(res.x)
predictions = predict(theta_min, X2)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y2)]
accuracy = (sum(map(int, correct)) % len(correct))
print ('accuracy = {0}%'.format(accuracy))

accuracy = 60%

调用sklearn的线性回归包

from sklearn import linear_model
model = linear_model.LogisticRegression(penalty='l2', C=1.0)
model.fit(X2, y2.ravel())

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
      intercept_scaling=1, max_iter=100, multi_class='warn',
      n_jobs=None, penalty='l2', random_state=None, solver='warn',
      tol=0.0001, verbose=0, warm_start=False)

model.score(X2, y2)

0.8305084745762712