小白式机器学习 (一) | logistic regression（LR）对数几率回归 / 逻辑回归公式推导

因为是傻瓜式教程，所以一定会非常详细！一些概念link到了Wiki的相应解释上。
欢迎捉虫~！

二分类和回归的关系

考虑 $\ x\Rightarrow y$ 表示的二分类或回归问题，其中 $\ x$ 是输入， $\ y$ 是输出。
1. 在二分类中， $\ y$ 的值取0或1，代表被分为正类或负类。在回归中， $\ y$ 的取值为连续值。
2. 在线性回归模型中， $\ y=w^{T} x= w\cdot x$ ，此处 $\ w$ 为参数向量， $\ x$ 为输入样本向量。
3. 进一步，广义线性回归模型可以写为 $\ g(y)=w\cdot x$ 或者 $\ y=g^{-1}(w\cdot x)$ 的形式，其中 $\ g$ 为单调可微函数。所以在对数回归中，模型是 $\ ln(y)=w\cdot x$ 。

sigmoid函数与LR的关系

sigmoid函数：在数学上是拥有性感的s形曲线样子的函数:
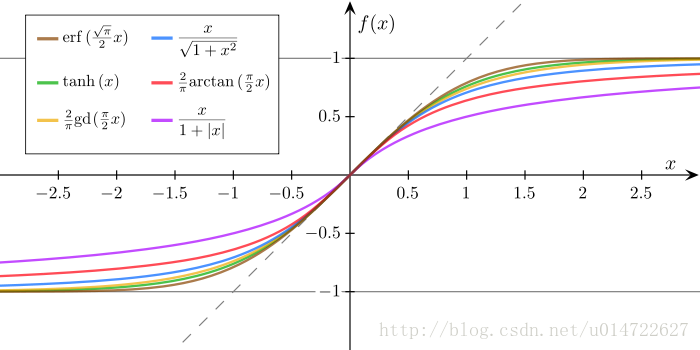
这里写图片描述

通常说的sigmoid函数指的是这个logistic函数： $\ \delta(z)=\frac{1}{1+e^{-z}} =\frac{e^{z}}{1+e^{z}}$ 。本文所指的sigmoid函数就是该logistic函数：
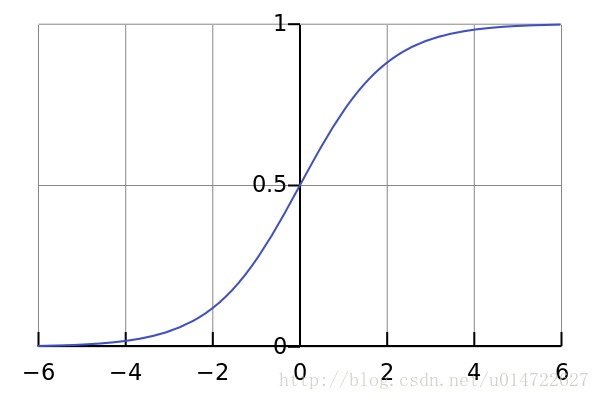
这里写图片描述

sigmoid函数具有以下特点：
- 值域在(0,1)
- 求导非常容易 $\ \delta'(z)=\delta(1-\delta(z))$ (求导过程见附录，或Wiki)

我们希望在做二分类时，输出 $\ y$ 不再是非0即1的取值，而是希望输出一个有概率意义的 $\ (0,1)$ 之间的值，表示的是分为正类的概率（所以 $\ 1-y$ 是分为负类的概率），然后再做二分类，所以我们挑选sigmoid函数作为广义线性回归的 $g^{-1}$ ，即

\begin{matrix} (1) & y = δ (w \cdot x) = \frac{1}{1 + e^{- w \cdot x}} \end{matrix}

$y=\delta (w\cdot x)=\frac{1}{1+e^{-w\cdot x}{}} \tag{1}$ 接下来将符合

y = g^{- 1} (w \cdot x)

$\ y=g^{-1}(w\cdot x)$ 形式的

(1)

$\ (1)$ 写为

g (y) = w \cdot x

$\ g(y)=w\cdot x$ 的形式，则

y + y e^{- w \cdot x} = 1

$y + ye^{-w\cdot x}=1$

y e^{- w \cdot x} = 1 - y

$ye^{-w\cdot x}=1-y$

e^{- w \cdot x} = \frac{1 - y}{y}

$e^{-w\cdot x}=\frac{1-y}{y}$

- w \cdot x = l n (\frac{1 - y}{y})

$-w\cdot x=ln(\frac{1-y}{y})$

\begin{matrix} (2) & w \cdot x = l n (\frac{y}{1 - y}) \end{matrix}

$w\cdot x=ln(\frac{y}{1-y}) \tag{2}$
所以，现在

g (y) = l n (\frac{y}{1 - y})

$\ g(y)=ln(\frac{y}{1-y})$ 。
前面说到，输出值

y

$\ y$ 代表分到正类的概率，

1 - y

$\ 1-y$ 代表分到负类的概率，那么

\frac{y}{1 - y} = \frac{正 类 概 率}{负 类 概 率}

$\ \frac{y}{1-y}=\frac{正类概率}{负类概率}$ ，称为几率，

l n (\frac{y}{1 - y})

$\ ln(\frac{y}{1-y})$ 称为 对数几率(logit)。

(2)

$\ (2)$ 的本质是用

w \cdot x

$\ w\cdot x$ 线性回归模型逼近对数几率，我们管这叫 对数几率回归( logit regression / logistics regression)。

条件概率

$\ y$ 代表分到正类的概率，即为条件概率： $\ P(y=1| x)$ 。
$\ 1-y$ 代表分到负类的概率，即为条件概率： $\ P(y \not=1| x) =P(y =0| x)= 1-P(y=1| x)$ 。
我们有 $P(y=1| x)=y=\frac{1}{1+e^{-w\cdot x}{}}$
假设数据集共有 $\ N$ 个样本，记第i个样本输入（m维向量）和样本标签分别为 $\ x_i =[x_{i(1)},x_{i(2)},...,x_{i(m)}]^T，y_i=\{0,1\}$ 。条件概率其实和参数 $\ w$ 有关，那么正确分类的条件概率应该写为: $\ P(y=y_i| x=x_i;w)$ ，简记为 $\ P(y_i| x_i;w)$ 。
(意思是输入变量 $\ x$ 取 $\ x_i$ 时，输出 $\ y$ =真实标签 $\ y_i$ 的概率)
$正确分类概率P(y_i| x_i;w)= \begin{cases} P(y=1| x_i;w), & \text{if $y_i=1$ } \\[2ex] P(y=0|x_i;w)=1-P(y=1| x_i;w), & \text{if $y_i =0$} \end{cases}$
$ln[P(y_i| x_i;w)]= \begin{cases} ln[P(y=1| x_i;w)], & \text{if $y_i=1$ } \\[2ex] ln[[P(y=0|x_i;w)]=ln[1-P(y=1| x_i;w)], & \text{if $y_i =0$} \end{cases}$
也等价于 $lnP(y=y_i| x_i;w)=\{y_i=1\}lnP(y=1| x_i;w)+\{y_i=0\}ln(1-P(y=1| x_i;w))$
其中 $\{y_i=1\}$ 称为示性函数，当条件被满足就取1，否则取0。
在二分类型况下，怎么样的函数能满足这样的条件呢？ $y_i$ 和 $1-y_i$ 就可以呀！
$\begin{matrix} (3) & l n [P (y_{i} | x_{i}; w)] = (y_{i}) l n [P (y = 1 | x_{i}; w)] + (1 - y_{i}) l n [1 － P (y = 1 | x_{i}; w)] \end{matrix}$ $ln[P(y_i|x_i;w)]=(y_i)ln[P(y=1|x_i;w)]+(1-y_i)ln[1－P(y=1|x_i;w)] \tag{3}$

从原始概率来看，即

P (y_{i} | x_{i}; w) = P (y = 1 | x_{i}; w)^{y_{i}} \times (1 - P (y = 1 | x_{i}; w))^{(1 - y_{i})}

$P(y_i| x_i;w)=P(y=1| x_i;w)^{y_i}\times(1-P(y=1| x_i;w))^{(1-y_i)}$

最大似然求解

似然的解释见附录或Wiki

我们希望，求得参数 $\ w$ ，使“抽取的样本 $\ x_i$ 属于本身的标签 $\ y_i$ 的概率最大 ”即 $\ P(y_i| x_i;w)$ 尽量大。
换句话说，就是极大化对数似然 $\ L(w)$ ：

\begin{matrix} (4) & L (w) = l n \prod_{i}^{N} P (y_{i} | x_{i}; w) = \sum_{i}^{N} l n [P (y_{i} | x_{i}; w)] \end{matrix}

$L(w)=ln \prod_i^N P(y_i| x_i;w)=\sum_i^N ln[ P(y_i| x_i;w) ] \tag{4}$
那么我们的目标就是

w^{*} = \underset{w}{a} r g m a x L (w)

$w^*=\underset{w}argmax L(w)$

(4)

$\ (4)$ 中我们用到

l n (a b) = l n (a) + l n (b)

$\ ln(ab)=ln(a) + ln(b)$ ，是因为连乘比起连加，求最优的难度更大，所以用对数函数转换一下，方便求解。
将

(3)

$(3)$ 带入

(4)

$(4)$ ，得：

\begin{matrix} (5) & L (w) = \sum_{i}^{N} l n [P (y = 1 | x_{i}; w)^{y_{i}} \times (1 - P (y = 1 | x_{i}; w))^{(1 - y_{i})}] \end{matrix}

$L(w)=\sum_i^N ln[P(y=1| x_i;w)^{y_i}\times(1-P(y=1| x_i;w))^{(1-y_i)}] \tag{5}$
化简：

L (w) = \sum_{i}^{N} {l n [P (y = 1 | x_{i}; w)^{y_{i}}] + l n [(1 - P (y = 1 | x_{i}; w)^{(1 - y_{i})}]}

$L(w)=\sum_i^N \left \{ ln[P(y=1| x_i;w)^{y_i}]+ln[(1-P(y=1| x_i;w)^{(1-y_i)}] \right \}$

L (w) = \sum_{i}^{N} {y_{i} l n [P (y = 1 | x_{i}; w)] + (1 - y_{i}) l n [1 - P (y = 1 | x_{i}; w)]}

$L(w)=\sum_i^N \left \{ y_iln[P(y=1| x_i;w)]+(1-y_i)ln[1-P(y=1| x_i;w)] \right \}$
我们有

P (y = 1 | x; w) = y = \frac{1}{1 + e^{- w \cdot x}}

$P(y=1| x;w)=y=\frac{1}{1+e^{-w\cdot x}{}}$

L (w) = \sum_{i}^{N} {y_{i} l n (\frac{P (y = 1 | x_{i}; w)}{1 - P (y = 1 | x_{i}; w)}) + l n (1 - \frac{e^{w \cdot x_{i}}}{1 + e^{w \cdot x_{i}}})}

$L(w)=\sum_i^N \left \{ y_i ln(\frac{P(y=1| x_i;w)}{1-P(y=1| x_i;w)})+ln(1-\frac{e^{w\cdot x_i}}{1+e^{w\cdot x_i}}) \right \}$
回忆

(2) ， l n (\frac{P (y = 1 | x_{i}; w)}{1 - P (y = 1 | x_{i}; w)})

$(2)，ln(\frac{P(y=1| x_i;w)}{1-P(y=1| x_i;w)})$ 实际就是

w \cdot x_{i}

$w\cdot x_i$ 嘛！

L (w) = \sum_{i}^{N} {y_{i} w \cdot x_{i} - l n (1 + e^{w \cdot x_{i}})}

$L(w)=\sum_i^N \left \{ y_iw\cdot x_i - ln(1+e^{w\cdot x_i})\right \}$

\begin{matrix} (6) & w^{*} = \underset{w}{a} r g m a x L (w) = \underset{w}{a} r g m i n [- L (w)] = \underset{w}{a} r g m i n \sum_{i}^{N} {l n (1 + e^{w \cdot x_{i}}) - y_{i} w \cdot x_{i}} \end{matrix}

$w^*=\underset{w}argmax L(w)=\underset{w}argmin [-L(w)]=\underset{w}argmin \sum_i^N \left \{ ln(1+e^{w\cdot x_i})-y_iw\cdot x_i \right \} \tag{6}$

最终目标函数成了最小化这个loss了，如何最小化？它关于x可导又连续，学过凸优化的都知道怎么做了吧？牛顿法、梯度下降等可以迭代求解最优。从搞神经网络的角度看，sigmoid是经典的激活函数，LR完全可以等价成一层的神经网络，激活函数是sigmoid！这里回忆一下，sigmoid函数的优良性质之一：导数好求。所以对于一切需要求梯度的方法，代码实现的难度就降低了。

附录

sigmoid函数求导

记 $\ f= \delta(x)$

f = \frac{1}{1 + e^{- x}} = \frac{e^{x}}{e^{x} + 1}

$f=\frac{1}{1+e^{-x}}=\frac{e^x}{e^x+1}$

\frac{1}{f} - 1 = \frac{e^{x} + 1}{e^{x}} - 1 = e^{x}

$\frac{1}{f}-1=\frac{e^{x}+1}{e^{x}}-1=e^x$

求 导 公 式 ： (\frac{1}{f})^{'} = - \frac{1}{f^{2}}; g (f)^{'} = g^{'} f \cdot f^{'}

$求导公式： (\frac{1}{f})'=-\frac{1}{f^2} ;\ g(f)'=g'f\cdot f'$

f^{'} = \frac{1}{(1 + e^{- x})^{2}} e^{- x} = f^{2} (\frac{1}{f} - 1) = f (1 - f)

$f'=\frac{1}{(1+e^{-x})^2} e^{-x}=f^2(\frac{1}{f}-1)=f(1-f)$

似然

我们从机器学习的角度看

记 $\theta$ 为模型（参数）。
记 $D$ 为训练数据集，是真实数据空间的抽样集合，训练数据集越大，D的分布越接近真实数据空间的分布。
记 $x$ 为一个观测，也可以理解为一个训练样本，是真实数据空间的一个抽样，即随机变量X的一个取值。
似然/似然函数（likelihood）：给定参数时，事件出现的可能性。
“似然”和“概率”可以算作同义词。通常，似然用于数据已知时描述模型参数（数据已知了还要描述数据出现的可能性，可不是就和参数有关嘛）。而概率通常用于描述未知的事件出现的可能性。似然的举例如下：
1. 当假设数据集中的每个样本在样本空间中都是独立的时候，参数 $\theta$ 相对于样本集 $D=\{x_1,x_2,x_3,...,x_n\}$ 的似然为 $L(\theta)=P(x_1,x_2,x_3,...,x_n|\theta)=\prod_i^nP(x_i|\theta)$
2. 参数 $\theta$ 相对于一个观测 $x$ 的似然为 $L(\theta)=P(x|\theta)$
$L(\theta)$ 是一个关于 $\theta$ 的函数。特别的，当 $\theta$ 是随机变量时， $L(\theta)$ 是条件概率 $P(X=x|\theta)$ ，也可以写为 $P(X=x;\theta)$ 。
贝叶斯推理的观点：
$\theta$ 是服从分布 $p_\theta$ 的随机变量，分布 $p_\theta$ 是关于模型的假设，称为先验，先验概率（piror probability）也记为 $p(\theta)$ ；给定数据集能得到模型 $\theta$ 的概率 $P(\theta|D)$ 称为后验概率（posterior probability）；参数 $\theta$ 下数据集样本都在观测都出现的概率 $P(x|\theta)$ 为似然（likelihood）；数据集的联合概率为 $P(D)$ 。

Reference：

周志华－《机器学习》
ufldl － softmax
图片均来自维基百科