《机器学习公式推导与代码实现》chapter17-kmeans

《机器学习公式推导与代码实现》学习笔记，记录一下自己的学习过程，详细的内容请大家购买作者的书籍查阅。

聚类分析和k均值聚类算法

聚类分析(cluster analysis)是一类经典的无监督学习算法，在给定样本的情况下，聚类分析通过度量特征相似度或者距离，将样本自动划分为若干类别。

1 距离度量和相似度度量方式

距离度量和相似度度量是聚类分析的核心概念，大多数聚类算法建立在距离度量之上。常用的距离度量方式包括闵氏距离和马氏距离，常用的相似度度量方式包括相关系数和夹角余弦等。

(1) 闵氏距离即闵可夫斯基距离(Minkowski distance)，该距离定义如下，给定m维向量样本集合X，对于xi，xj∈X，xi=(x1i,x2i,...xmi)T，那么样本xi与样本xj的闵氏距离可定义为：
$$d_{ij}={\left(\sum _{k=1}^m{\left|x_{ki}-x_{kj}\right|}^p\right)}^{\frac{1}{p}},p\ge 1$$
可以简单看出，当p=1时，闵氏距离就变成了曼哈顿距离(Manhatan distance)：
$$d_{ij}=\sum _{k=1}^m\left|x_{ki}-x_{kj}\right|$$
当p=2时，闵氏距离就变成了欧氏距离(Euclidean distance)：
$$d_{ij}={\left(\sum _{k=1}^m{\left|x_{ki}-x_{kj}\right|}^2\right)}^{\frac{1}{2}}$$
当p=∞时，闵氏距离也称切比雪夫距离(Chebyshev distance)：
$$d_{ij}=max\left|x_{ki}-x_{kj}\right|$$
(2) 马氏距离全称马哈拉诺比斯距离(Mahalanobis distance)，是一种衡量各个特征之间相关性的聚类度量方式。给定一个样本集合X=(xij)mxn，假设样本的协方差矩阵为S，那么样本xi与样本xj之间的马氏距离可以定义为：
$$d_{ij}={\left[{\left(x_i-x_j\right)}^T{S}^{-1}\left(x_i-x_j\right)\right]}^{\frac{1}{2}}$$
当S为单位矩阵，即样本的各特征之间相互独立且方差为1时，马氏距离就是欧氏距离。

(3) 相关系数(correlation coefficent)是度量样本相似度最常用的方式。相关系数有多种定义方式，较为常用的是皮尔逊相关系。相关系数越接近1，两个样本越相似；样本xi与样本xj之间的相关系数可定义为：
$$r_{ij}=\frac{{\sum }_{k=1}^m\left(x_{ki}-{\bar{x}}_i\right)\left(x_{kj}-{\bar{x}}_j\right)}{{\left[{\sum }_{k=1}^m{\left(x_{ki}-{\bar{x}}_i\right)}^2{\sum }_{k=1}^m{\left(x_{kj}-{\bar{x}}_j\right)}^2\right]}^{\frac{1}{2}}}$$
上边这个式子看起来有点复杂，其实就是：
$$r\left(X,Y\right)=\frac{Cov\left(X,Y\right)}{\sqrt{Var\left[X\right]Var\left[Y\right]}}$$
(4) 余弦夹角(angle cosine)也是度量两个样本相似度的方式。夹角余弦越接近1，表示两个样本越相似:
$$similarity=cos\left(\theta \right)=\frac{A\cdot B}{\Vert A\Vert \Vert B\Vert }$$
样本xi与样本xj之间的夹角余弦可定义为：
$$A{C}_{ij}=\frac{{\sum }_{k=1}^m{x}_{ki}{x}_{kj}}{{\left[{\sum }_{k=1}^m{x}_{ki}^2{\sum }_{k=1}^m{x}_{kj}^2\right]}^{\frac{1}{2}}}$$

2 聚类算法一览

聚类算法将相似的样本归入同一个簇(cluster)中，这使得同一个簇中的样本对象的相似度尽可能大，同时不同簇中的样本对象的差异性也尽可能大。常用的聚类算法有如下几种：

• 基于距离的聚类:该类算法的目标是使簇内距离小、簇间距离大，最典型的就是k均值聚类算法。
• 基于密度的聚类:该类算法是根据样本邻近区域的密度来进行划分的，最常见的密度聚类算法当属DBSCAN算法。
• 层次聚类算法:包括合并层次聚类和分裂层次聚类等。
• 基于图论的谱聚类。

sklearn在不同数据集上的10类聚类算法效果对比。

3 K-means算法原理

4 K-means算法numpy实现

import numpy as np

# 定义欧氏距离
def euclidean_distance(x, y):
    
    distance = 0
    for i in range(len(x)):
        distance += np.power((x[i] - y[i]), 2)
    return np.sqrt(distance)

# 质心初始化
def centroids_init(X, k): # 训练样本,质心个数(聚类簇数）

    m, n = X.shape # 样本数和特征数
    centroids = np.zeros((k, n)) # 初始化质心矩阵，大小为质心个数*特征数
    for i in range(k):
        centroid = X[np.random.choice(range(m))]
        centroids[i] = centroid
    return centroids # centroids：质心矩阵,k个长度为n的从m个样本中选取的样本

# 求单个样本所属最近质心的索引
def closest_centroid(x, centroids): # 单个样本实例，质心矩阵

    closest_i, closest_dist = 0, float('inf')
    for i, centroid in enumerate(centroids):
        distance = euclidean_distance(x, centroid)
        if distance < closest_dist:
            closest_i = i
            closest_dist = distance
    return closest_i # closest_i：最近质心

# 构建簇与分配样本
def build_clusters(centroids, k, X): # 质心矩阵,质心个数, 训练样本

    clusters = [[] for _ in range(k)] # 初始化簇列表
    for x_i, x in enumerate(X):
        centroid_i = closest_centroid(x, centroids) # 样本最近质心的下标
        clusters[centroid_i].append(x_i) # 样本下标加入簇矩阵中
    return clusters # 聚类簇

# 计算新的质心
def calculate_centroids(clusters, k, X):

    n = X.shape[1] # 特征数
    centroids = np.zeros((k, n)) # 初始化质心矩阵
    for i, cluster in enumerate(clusters):
        centroid = np.mean(X[cluster], axis=0) # 计算每个簇的均值作为新的质心
        centroids[i] = centroid # 更新质心矩阵
    return centroids # 返回新的质心矩阵

# 获取每个样本所属聚类类别
def get_cluster_labels(clusters, X):

    y_pred = np.zeros(X.shape[0]) # 样本数
    for cluster_i, cluster in enumerate(clusters):
        for sample_i in cluster:
            y_pred[sample_i] = cluster_i
    return y_pred # 预测结果

# 封装k-means算法
def kmeans(X, k, max_iterations):

    centroids = centroids_init(X, k) # 训练样本,质心个数(聚类簇数）

    # 迭代至收敛
    for _ in range(max_iterations):
        clusters = build_clusters(centroids, k, X) # 分配样本与构建簇
        new_centroids = calculate_centroids(clusters, k, X) # 计算新的质心
        print(f'迭代进行到第{
      
      _}轮')
        diff = centroids - new_centroids
        centroids = new_centroids
        if not diff.any():
            break
    return get_cluster_labels(clusters, X) # 获取每个样本所属聚类类别

from sklearn import datasets

# 测试算法
data = datasets.load_iris()
iris, y = data.data, data.target
label_pred = kmeans(iris, 3, 100)

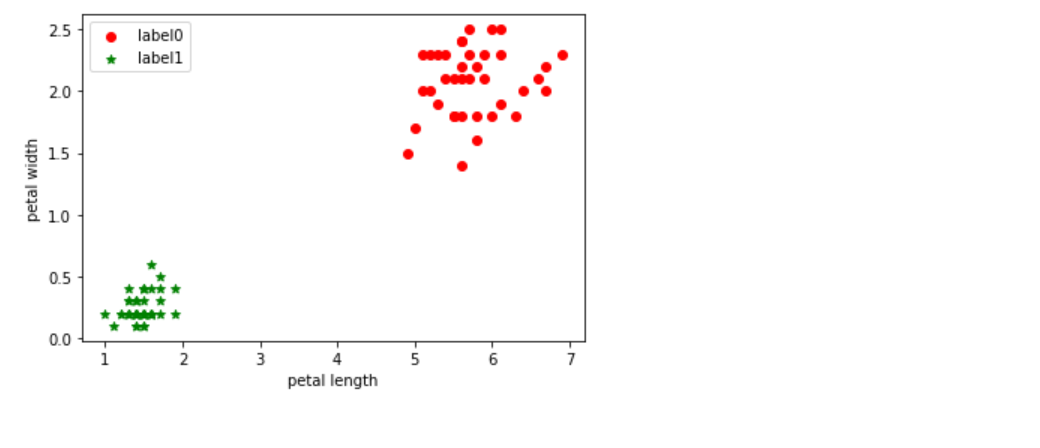
# 取2个或者3个维度来看一下聚类的效果
X = iris[:,2:]
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
plt.scatter(x0[:, 0], x0[:, 1], c = "red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c = "green", marker='*', label='label1')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()

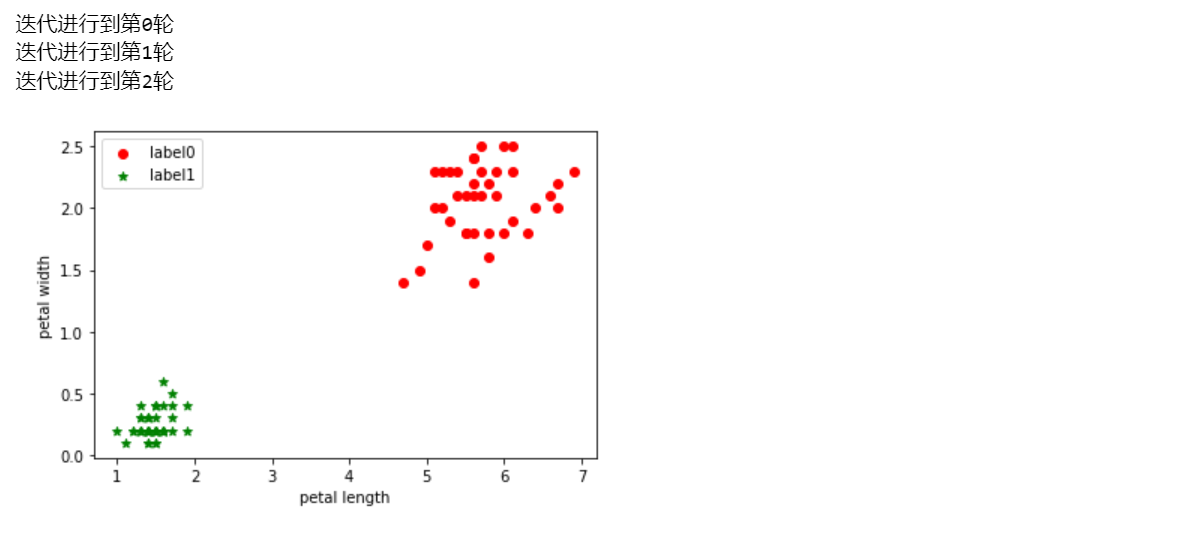
5 基于sklearn的K-means算法

from sklearn.cluster import KMeans

kmeans_sk = KMeans(n_clusters=3, random_state=2023).fit(iris)
label_pred = kmeans_sk.labels_ # 打印拟合标签

X = iris[:,2:]
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
plt.scatter(x0[:, 0], x0[:, 1], c = "red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c = "green", marker='*', label='label1')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()

笔记本_Github地址