【机器学习笔记】第4章：Logistic回归

第4章：Logistic回归

4.1 分类 Classification

我们考虑要预测的变量y是一个离散值情况下的分类问题。例如对肿瘤进行分类，判断是恶性肿瘤还是良性肿瘤。我们尝试预测的变量y可以有两个取值 $y\in\{0,1\}$，用0表示负类，用1表示正类，称为二分类或者二元分类。y还可以有多个取值，如 $y\in\{0,1,2,3\}$，称为多元分类。
Logistic回归算法是一种分类算法，它的预测值一直介于0和1之间。

4.2 假设陈述 Hypothesis representation

线性回归的假设函数为 $h_\theta(x)=\theta^Tx=\theta_0x_0+\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n$
将一个Sigmoid function（或叫Logistic function） $g(z)=\frac{1}{1+e^{-z}}$作用在线性回归的假设函数上，就得到了逻辑回归的假设函数： $h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}$
假设函数得到的预测值的含义可以用数学式表达 $h_\theta(x)=P(y=1|x;\theta)$，即在给定特征x的条件下y=1的概率；同理，有 $h_\theta(x)=P(y=0|x;\theta)$。
因为y只能等于0和1，所以有： $P(y=0|x;\theta)+P(y=1|x;\theta)=1$ $P(y=0|x;\theta)=1-P(y=1|x;\theta)$

4.3 决策界限 Decision boundary

逻辑回归的假设函数输出的是给定x和参数 $\theta$时y=1的估计概率，因此，根据Sigmoid函数曲线图，我们想预测y=1还是y=0取决于 $g(\theta^Tx)$是大于等于0.5还是小于0.5。
根据Sigmoid函数曲线图可知，
要使 $g(\theta^Tx)\geq0.5$，只需 $\theta^Tx\geq0$
要使 $g(\theta^Tx)<0.5$，只需 $\theta^Tx<0$

例如，现在假设我们有一个训练集，它的假设函数为 $h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2)$，假设我们已经拟合好了参数，比方说选择 $\theta_0=-3,\theta_1=1,\theta_2=1$，我们试着找出假设函数何时将预测y等于1，何时又将预测y等于0。
要使 $g(-3+x_1+x_2)\geq0.5$，只要满足 $-3+x_1+x_2\geq0$，即 $x_1+x_2\geq3$时， $y=1$
要使 $g(-3+x_1+x_2)<0.5$，只要满足 $-3+x_1+x_2<0$，即 $x_1+x_2<3$时， $y=0$
这里的 $x_1+x_2=3$就称为决策边界。

注意，决策边界是假设函数的一个属性，决策边界取决于其参数 $\theta$，它不是数据集的属性。
一旦我们用训练集拟合好参数 $\theta$，就将完全确定决策边界。

另外，我们还可以在假设函数的特征中引入额外的高阶多项式项。例如，假设函数为 $h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_2^2)$，假设我们已经拟合好了参数，比方说选择 $\theta_0=-1,\theta_1=0,\theta_2=0,\theta_3=1,\theta_4=1$，要使 $g(-1+x_1^2+x_2^2)\geq0.5$，只要满足 $-1+x_1^2+x_2^2\geq0$，即 $x_1^2+x_2^2\geq1$时， $y=1$，那么决策边界就是半径为1原点为中心的圆。

4.4 代价函数 Cost function

逻辑回归模型的参数拟合问题，就是定义用来拟合参数的代价函数。

在这里我们不能直接使用线性回归的代价函数，因为Sigmoid函数是非线性函数，得到的代价函数图像是一个非凸函数，如果把梯度下降法应用到这样的函数上，不能保证它会收敛到全局最小值。

逻辑回归的代价函数： $J(\theta)=\frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)})$ $Cost(h_\theta(x),y)= \begin{cases} -log(h_\theta(x)) &if \quad y=1\\ -log(1-h_\theta(x)) &if \quad y=0 \end{cases}$
当真实值y=1时，代价函数图像如下图所示，如果假设函数预测值 $h_\theta(x)=1$，则与真实值y相同，代价为0；如果假设函数预测值 $h_\theta(x)=0$，则代价非常大。比如我们预测一个病人有恶性肿瘤的概率为0，然而病人的肿瘤确实是恶性的，那么我们用非常大的代价来惩罚这个学习算法。

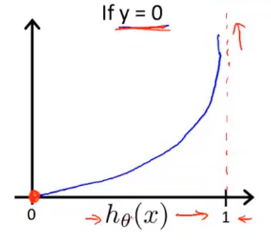
当真实值y=0时，代价函数图像如下图所示。

4.5 简化代价函数与梯度下降 Simplified cost function and gradient descent

因为y的取值只有0和1，所以我们可以简化代价函数为：
$J(\theta) = \frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)})$ $Cost(h_\theta(x^{(i)}),y^{(i)})= -y^{(i)}log(h_\theta(x^{(i)}))-(1-y^{(i)})log(1-h_\theta(x^{(i)}))$
综合以上式子，得： $J(\theta) = -\frac{1}{m}[\sum_{i=1}^my^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)}))]$
根据这个代价函数，为了拟合出参数，我们要找出使得 $J(\theta)$取得最小值的参数 $\theta$。最小化代价函数的方法是使用梯度下降法。

另外，之前线性回归中提到的特征缩放可以提高梯度下降收敛的速度，也同样适用于Logistic回归。如果特征范围差距很大的话，那么应用特征缩放的方法，同样也可以让Logistic回归中的梯度下降收敛更快。

4.6 高级优化 Advanced optimization

高级优化算法相比于梯度下降，能大大提高Logistic回归运行的速度，这也使得高级优化算法更适用于解决大型机器学习问题。
要得到 $J(\theta)$及其偏导，除了梯度下降外,还有共轭梯度法、BFGS、L-BFGS，这三种算法的优点：
1.不需要手动选择学习率 $\alpha$
2.收敛速度远远快于梯度下降
缺点：比梯度下降算法要复杂的多

下面举例说明用高级优化算法优化二阶代价函数。例如，有一个含有两个参数的问题，代价函数为 $J(\theta)=(\theta_1-5)^2+(\theta_2-5)^2$，如果要将代价函数 $J(\theta)$最小化的话，直接求导 $\frac{\partial}{\partial \theta_1}J(\theta)=2(\theta_1-5),\frac{\partial}{\partial \theta_2}J(\theta)=2(\theta_2-5)$即可找到最小值，但最好使用高级优化的方法。
首先我们在Octave里实现一个代价函数costFunction，如下图所示：

这个函数的作用是返回两个自变量，第一个自变量jVal是代价函数，第二个自变量Gradient是对代价函数求偏导后得到的2x1的向量。运行这个costFunction函数后，就可以调用高级的优化函数fminunc，它在Octave表示无约束最小化函数。options是一个可以存储你想要的options的数据结构，gradObj和on设置梯度目标参数为打开，MaxIter和100设置100为最大迭代次数，initialTheta定义二维向量 $\theta$的初始值，@costFunction是指向我们刚刚定义的代价函数costFunction的指针。
在Octave中运行结果如下：

结果得到了 $\theta$的最优值，functionVal=10的-30次方就相当于0，exitFlag=1说明已经收敛。
下面用优化算法优化Logistic回归。

4.7 多元分类：一对多 Multi-class classification:one-vs-all

一对多分类的原理：
假设我们有一个训练集包含三个类别，用三角形表示y=1，方形表示y=2，交叉表示y=3。我们要做的是将这个训练集转换成三个独立的二分类问题，拟合出三个标准的逻辑回归分类器： $h_\theta^{(i)}(x)=P(y=i|x;\theta)\quad(i=1,2,3)$

• $h_\theta^{(1)}(x)$：三角形是正样本
• $h_\theta^{(2)}(x)$：方形是正样本
• $h_\theta^{(3)}(x)$：交叉是正样本
  
  即我们训练了一个逻辑回归分类器 $h_\theta^{(i)}(x)$预测i类别y=i的概率。当我们需要判别新的输入值x属于哪一类的时候，就分别在三个分类器中运行输入x，然后选择h最大的类别 $max_i h_\theta^{(i)}(x)$。