凸函数

今天主要来学习的是凸函数：包括是什么是凸函数，凸函数的判断，对于非凸函数的处理。

凸函数

先来看看什么是凸函数：

如图左边的是一个凸函数，右边的不是凸函数，从图片我们也可以清楚的看到凸函数的一个显著的特点，也就是对于凸函数来说只有一个最低点，也就是极值点就是最值点，而非凸函数有多个极值点。因此在人工智能领域，如果遇到一个问题，我们的目标函数是一个凸函数，也就是说我们可以找到一个全局的最优解，如果我们的目标函数是一个非凸函数，那么我们有可能找到的解只是局部最优解，而这显然不是我们想要的，我们再设计目标函数时一定要考虑目标函数是不是凸函数。

凸函数的判断

凸函数的前提条件

判断一个函数是不是凸函数有一个前提条件，如果满足我们在判断它是不是凸函数，如果不满足我们就可以直接否定了

前提条件就是判断目标函数的定义域是不是凸集。那么怎么判断一个函数的定义域是不是凸集呢？
定义：假设我们存在一个集合C，对于任意 $x,y\in C$来说我们有：

$a(x)+(1-a)y\in C$

解释一下：如图

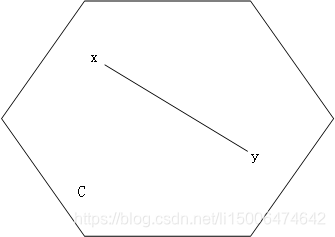
对于 $x,y$连线，能够保证线上的每一点都在集合C内，换句话说对于集合C内的任意两点之间的连线，保证每一点都在集合C内，我们就说集合C是一个凸集。

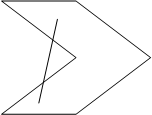
上图这种集合就不是一个凸集合

常见的凸集合：

所有 $R^n$

整数 $R^n$

范数 $||x||\leq1$

线性方程所有的解 $Ax=b$

两个凸集合的交集也是凸集合

定义判断函数是否是凸函数

若定义域是凸集合，那么我们可以判断该函数是不是凸函数了根据凸函数的定义：
若定义域是凸集合，那么对于定义域内的x，y满足：

$f(\theta x+(1-\theta)y)\leq\theta f(x)+(1-\theta)f(y)$ $\quad\theta\in[0,1]$

用几何的方式来解释的话就是如下图：

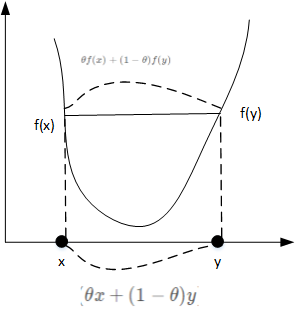
如上图所示 $\theta x+(1-\theta)y$表示的是 $x,y$之间的一点，
那么 $f(\theta x+(1-\theta)y)$表示的是 $f(x)和f(y)$在弧线上的任意一点， $\theta f(x)+(1-\theta)f(y)$表示 $f(x)和f(y)$之间的连线上的一点，
也就是 $f(x)和f(y)$之间的连线上的一点 $\geq$ $f(x)和f(y)$在弧线上的任意一点我们就说这个函数是凸函数。

求导判断凸函数

若 $f(x)$是可导的，那 $f(x)$是凸函数当且仅当：

$f(y)\geq f(x)+\nabla f(x)^T(y-x)$

无论什么情况下 $\nabla f(x)^T(y-x)$永远都在 $f(y)$下方我们定义 $f(x)$为凸函数。

当然最常用的还是下面这个定理：

若 $f(x)$是二次可导的，那 $f(x)$是凸函数当且仅当：

$\nabla ^2f(x)\geq0$

也就是目标函数的二阶导数如果大于0我们就认为这个函数是凸函数。

举个例子

现在有个全集 $U=\{1,2,3.4,5\}$以及子集合： $s_1(1,2,3),s_2(2,4),s_3(1,3),s_4(4),s_5(3,4),s_6(4,5)$求最少子集合，它们的并集为 $U$

对于这个问题我们使用3种方法：
暴力求解（枚举法）：
第一步：选择一个集合，查看是否符合为 $U$
第二步：选择全部两个集合的组合，查看并集是否符合为 $U$
第三步：选择全部三个集合的组合，查看并集是否符合为 $U$
以此类推
使用这个方法我们在第二步就计算出来为 $s_1,s_6$
优点：找到的是全局最优解
缺点：计算量太大

贪心算法：
第一步：选择所有集合，查看并集是否为 $U$
并集为 $U$
第二步：删除 $s_1$,查看并集是否为 $U$
并集为 $U$
第三步：删除 $s_2$,查看并集是否为 $U$
并集不为 $U$
第四步：删除 $s_3$,查看并集是否为 $U$
并集不为 $U$
第五步：删除 $s_4$,查看并集是否为 $U$
并集为 $U$
第6步：删除 $s_2$,查看并集是否为 $U$
以此类推最后那个就是我们使用贪心算法计算出来的最优解
结果是 $s_2,s_3,s_6$

很明显看出贪心算法得出来的不是最优解。

第三种方法：
设计目标函数，不断优化结果，直到找到最优解：
我们令 $x_i$表示 $s_i$有没有被选中，选中为1，没选中为0，所以 $x[0,1]$这个时候我们的目标函数为：

$minmize\quad\sum_i^mx_i$

条件为： $\sum_{i:e\in s_i}x_i\geq1$

$i:e\in s_i$表示为包含元素 $e$的子集合， $e\in U$

现在我们来判断这个函数是不是凸函数，

第一步，判断定义域是不是凸集

很明显定义域是一个离散型的，不是凸集，也就是说目标函数不是凸函数。
这个时候怎么办呢?
离散型的比较难计算，所以我们将目标函数松弛化，也就是将 $x[0,1]$改变为 $0\leq x\leq1$那么这个时候我们计算出来的结果是有可能是一个小数，这个时候我们就可以强行设置如： $x\geq 0.5$时 $x=1$, $x\leq 0.5$时 $x=0$