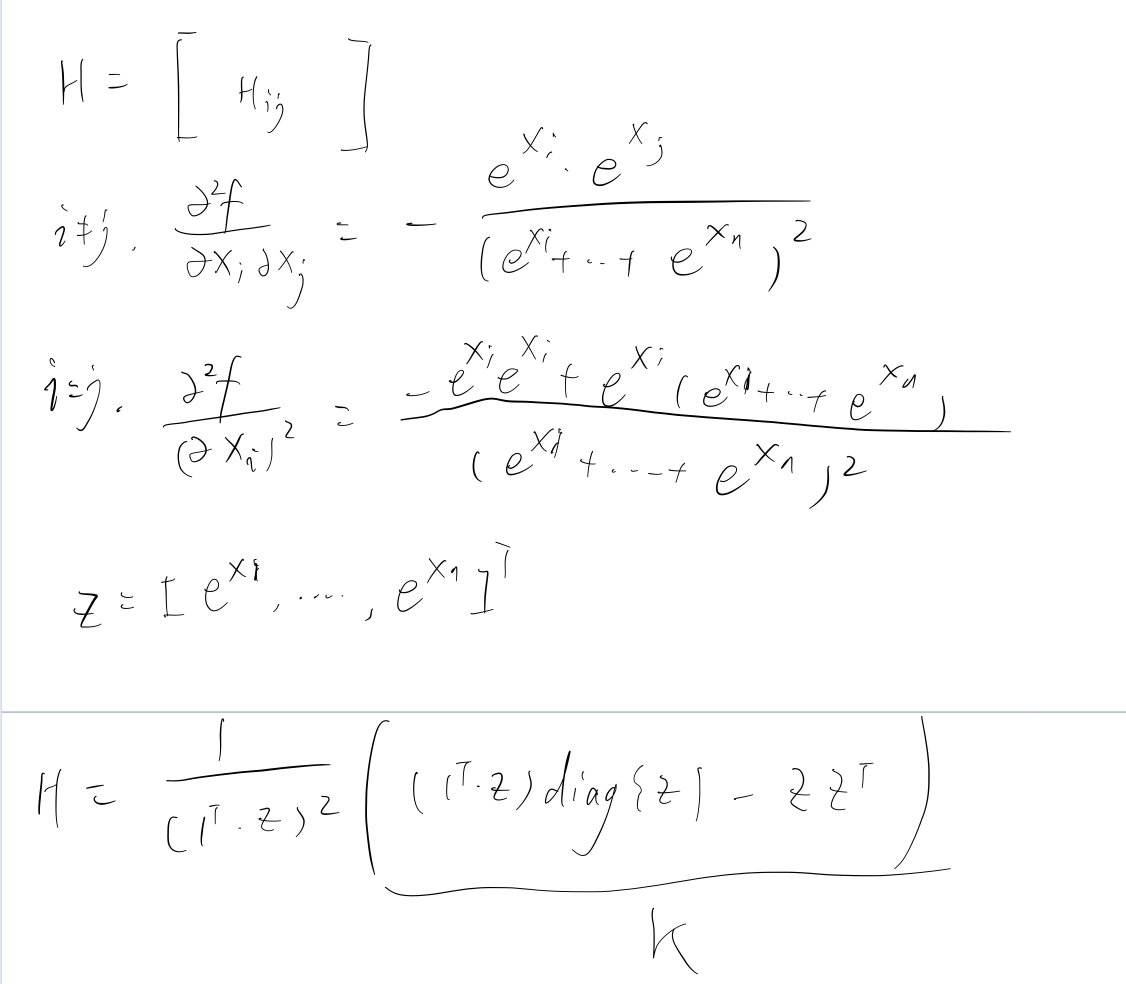引言
本文先介绍凸函数的4种定义方式,然后介绍一些凸函数。
凸函数的第一个定义
\(f: R^n \rightarrow R\)为凸函数,等价于:\(dom f\)为凸,且
\[\forall x,y \in dom f, 0 \leq \theta \leq 1\]
有
\[f(\theta x + (1-\theta)y) \leq \theta f(x) + (1 - \theta)f(y)\]
凸函数的第二个定义(高维情况下用的比较多)
若\(f:R^n \rightarrow R\)为凸,等价于:
\(dom f\)为凸,\(\forall x \in dom f, \forall v\),
\[g(t) = f(x + tv)\]
为凸函数,\(dom g=\{t|x+tv \in dom f\}\)
凸函数的第三个定义:一阶条件
设\(f: R^n \rightarrow R\)可微,即梯度\(\bigtriangledown f\)在\(dom f\)上均存在,则\(f\)为凸函数等价于:
\(dom f\)为凸。
\(f(y) \geq f(x) + \bigtriangledown f^T(x)(y-x), \forall x,y \in dom f\)
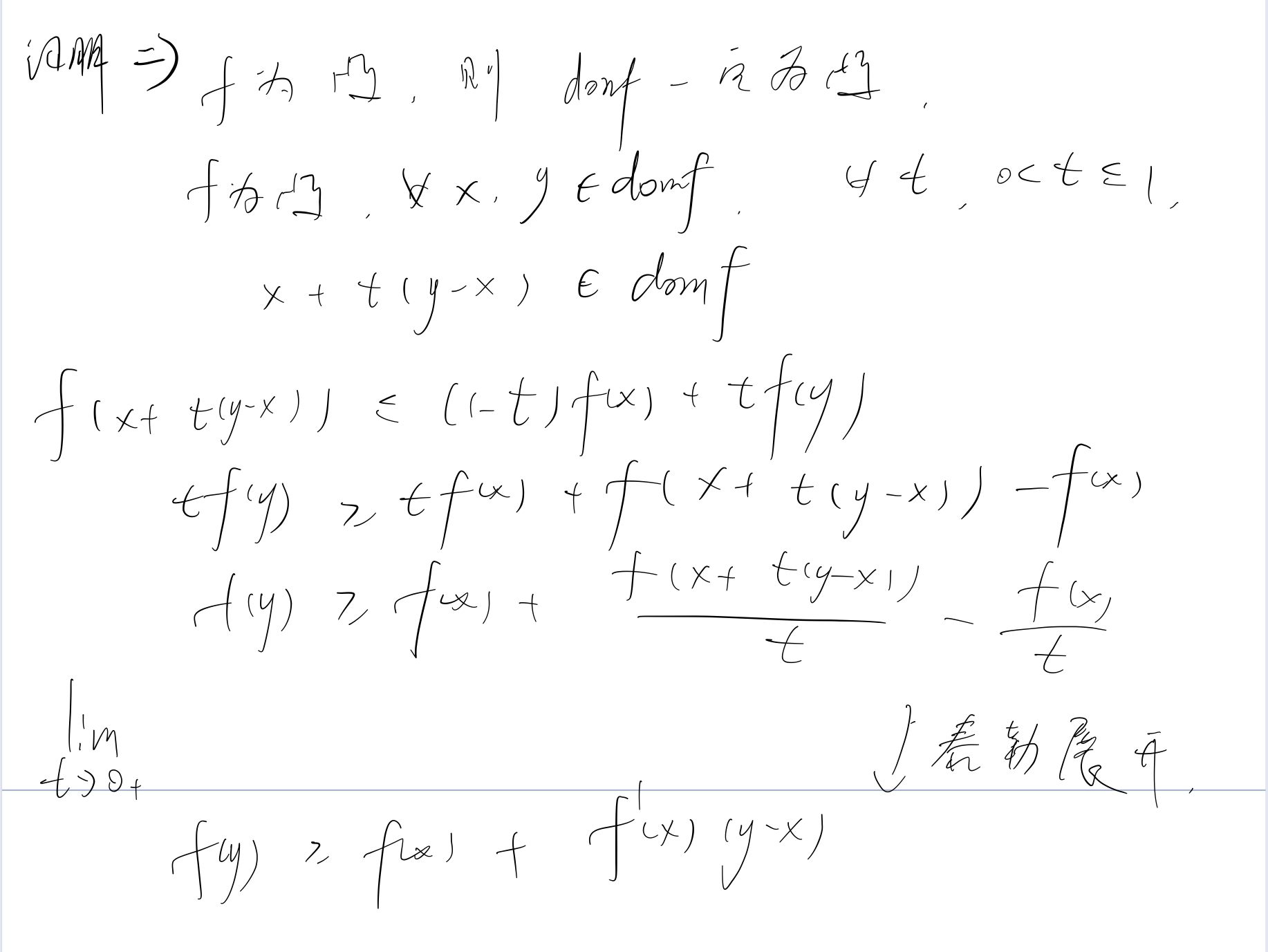
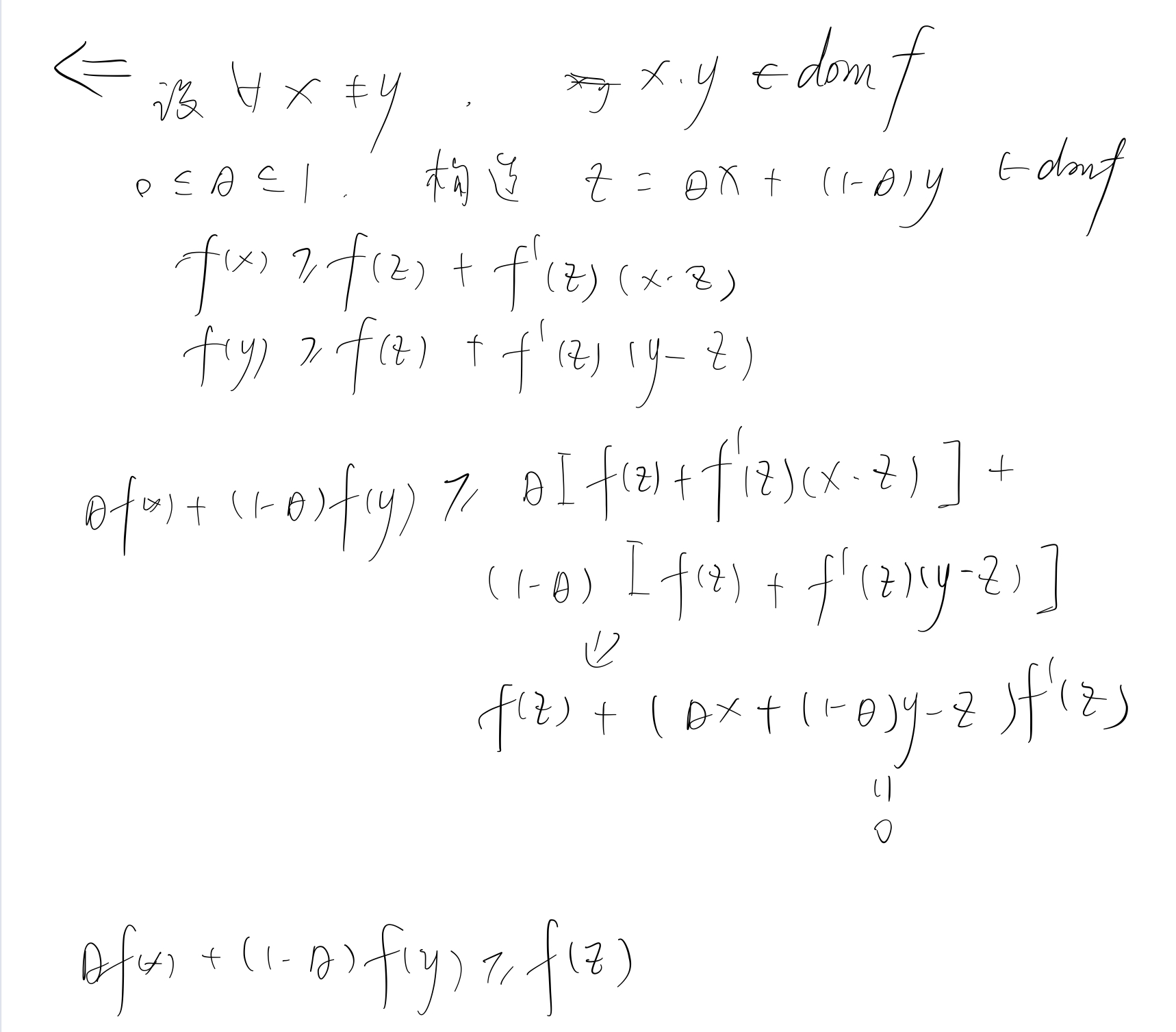


一些常见函数
二次函数
\[f: R^n \leftarrow R, dom f \in R^n\]
\[f(x)=\frac{1}{2}x^TPx + q^Tx + r\]
求其黑塞矩阵:\(\bigtriangledown^2 f(x)=P\),当\(P>0\)的时候,二次函数就是凸函数。
分数函数
\[f(x)=\frac{1}{x^2}, x \not= 0, x \in R\]
其二阶倒数\(f^{``}(x)=6x^{-4}>0\),虽然二阶导大于0,但是这个函数并不是凸函数。主要原因是因为:要定义域是凸集,且二阶导大于0的函数才是凸函数。这里定义域不是凸集。
仿射函数
\[f(x)=Ax + b, \bigtriangledown^2f(x)=0\]
故仿射函数即时凸函数,也是凹函数。
指数函数
\[f(x)=e^{ax}, x\in R\]
\[f^{``}(x)=a^2 e^{ax} > 0\]
故指数函数是凸函数。
幂函数
\[f(x)=x^a, x \in R_{++}\]
\[f^{``}(x)=a(a-1)x^{a-2}\]
\[ \bigtriangledown^2f(x) = \begin{cases} \geq 0, a \geq 1 或 a \leq 0 \\ \leq 0, 0 \leq a \leq 1 \end{cases} \]
绝对值幂函数
\[f(x) = |x|^p, x\in R\]
\[ f^{``}(x) = \begin{cases} p(p-1)x^{p-2}, x \geq 0 \\ p(p-1)(-x)^{p-2}, x < 0 \end{cases} \]
当\(p\geq 1\)时,该函数为凸函数。
对数函数
\[f(x)=log(x), x\in R_{++}\]
- 凹函数
负熵
\[f(x)=xlogx , x \in R_{++}\]
- 凸函数
范数
下面给出范数的定义:
\(R^n\)空间的范数\(p(x), x\in R^n\),满足三个性质:
- \(p(ax)=|a|p(x)\)
- \(p(x+y) \leq p(x)+p(y)\)
- \(p(x)=0 \leftrightarrows x=0\)
- 范数函数是凸函数。
零范数
零范数的定义是:\(||x||_0=非零元素的数目\)
- 该函数虽然名字有叫范数,但它不是范数,也不是凸函数。
极大值函数