凸函数与凸集

  对于《欠定线性系统与正则化》一节中的优化问题：

$(P_J):\min \limits_{\bf x} J({\bf x})\quad {\rm s.t.} \quad{\bf b=Ax}$

只要 $J(\cdot)$为严格凸的函数，都能保证只有唯一解， ${\mathcal l}_2$能够带来唯一解就是其中的一个例子。

1、凸集

【定义1】对于集合 $\Omega$， $\forall {\bf x}_1,{\bf x}_2\in \Omega$以及 $\forall t\in[0,1]$，若凸组合
${\bf x}=t{\bf x}_1+(1-t){\bf x}_2$也在 $\Omega$中，则 $\Omega$为凸集。

  显然，图1中的(a)为凸集，而(b)为凹集。

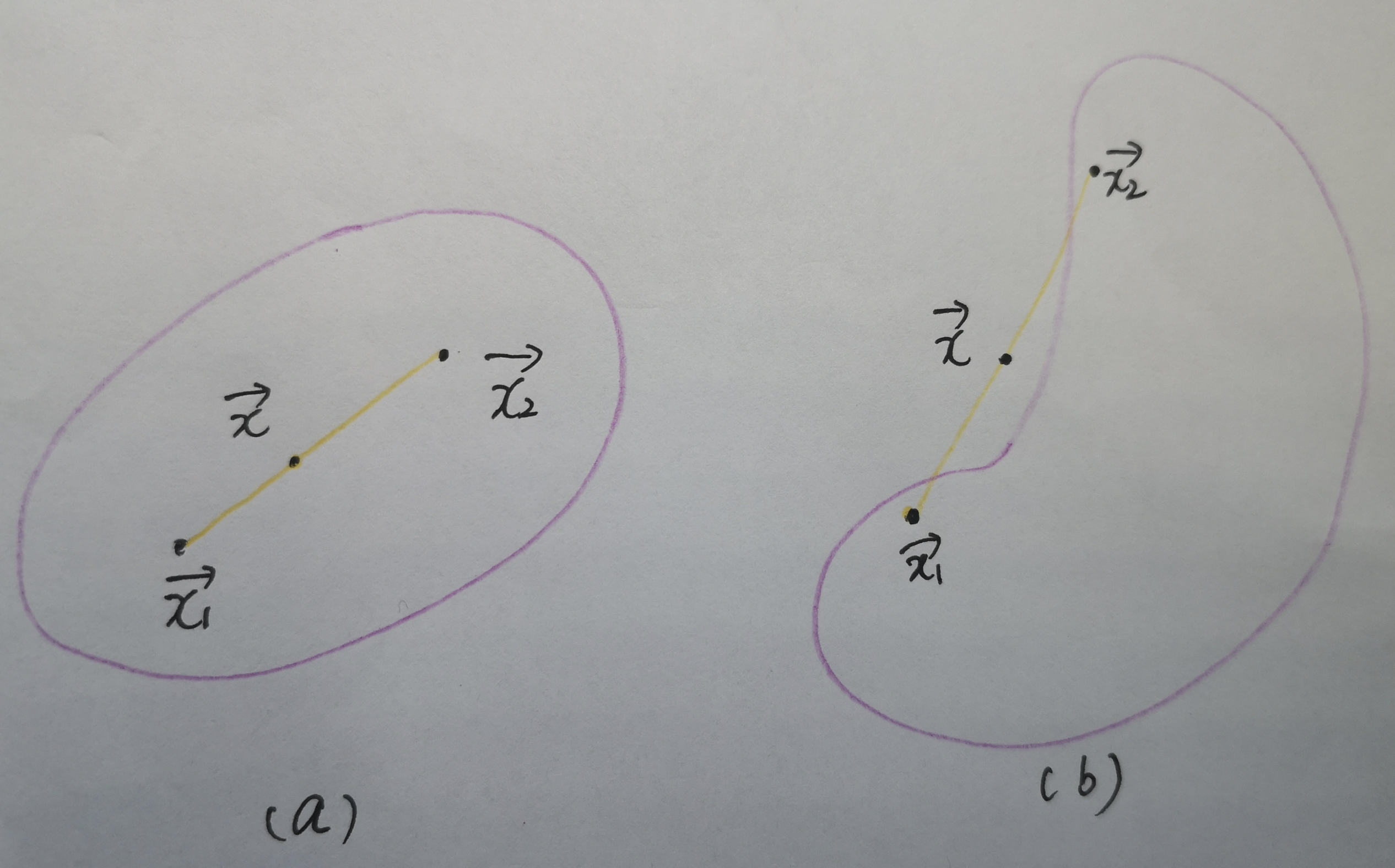
图1 凸集的定义

  下面我们用定义1来看看 ${\bf Ax=b}$的解集的凸性。设 $\Omega=\{{\bf x}|\bf Ax=b\}$，由 $\bf Ax=b$,可得 $\bf x=(A^{\rm T}A)^{-1}A^{\rm T}b$。显然， ${\bf x}=t{\bf x}_1+(1-t){\bf x}_2=\bf (A^{\rm T}A)^{-1}A^{\rm T}b\in \Omega$因此 ${\bf Ax=b}$的解集 $\Omega$为凸集。
  为了保证优化问题总体上是凸的，我们还必须保证惩罚函数 $J(\bf x)$也是凸的。所以我们先来看看凸函数的定义。

2、凸函数

【定义2】若函数 $J(\bf x):\Omega\rightarrow{\mathbb R}$为凸的，则 $\forall{\bf x}_1,{\bf x}_2\in \Omega$且 $\forall t\in[0,1]$，凸组合点 ${\bf x}=t{\bf x}_1+(1-t){\bf x}_2$满足
$J( t{\bf x}_1+(1-t){\bf x}_2)\le tJ({\bf x}_1)+(1-t)J({\bf x}_2).$

图2给出了凸函数的定义，从图中可以看出，当 $t$在0到1之间变化时， $\bf x$在 $\bf x_1$和 $\bf x_2$之间变化，而 $J( t{\bf x}_1+(1-t){\bf x}_2)$为函数 $J({\bf x})$上的点，它始终小于 $({\bf x}_1,J({\bf x}_1))$和 $({\bf x}_2,J({\bf x}_2))$两点连线上的点： $tJ({\bf x}_1)+(1-t)J({\bf x}_2)$。

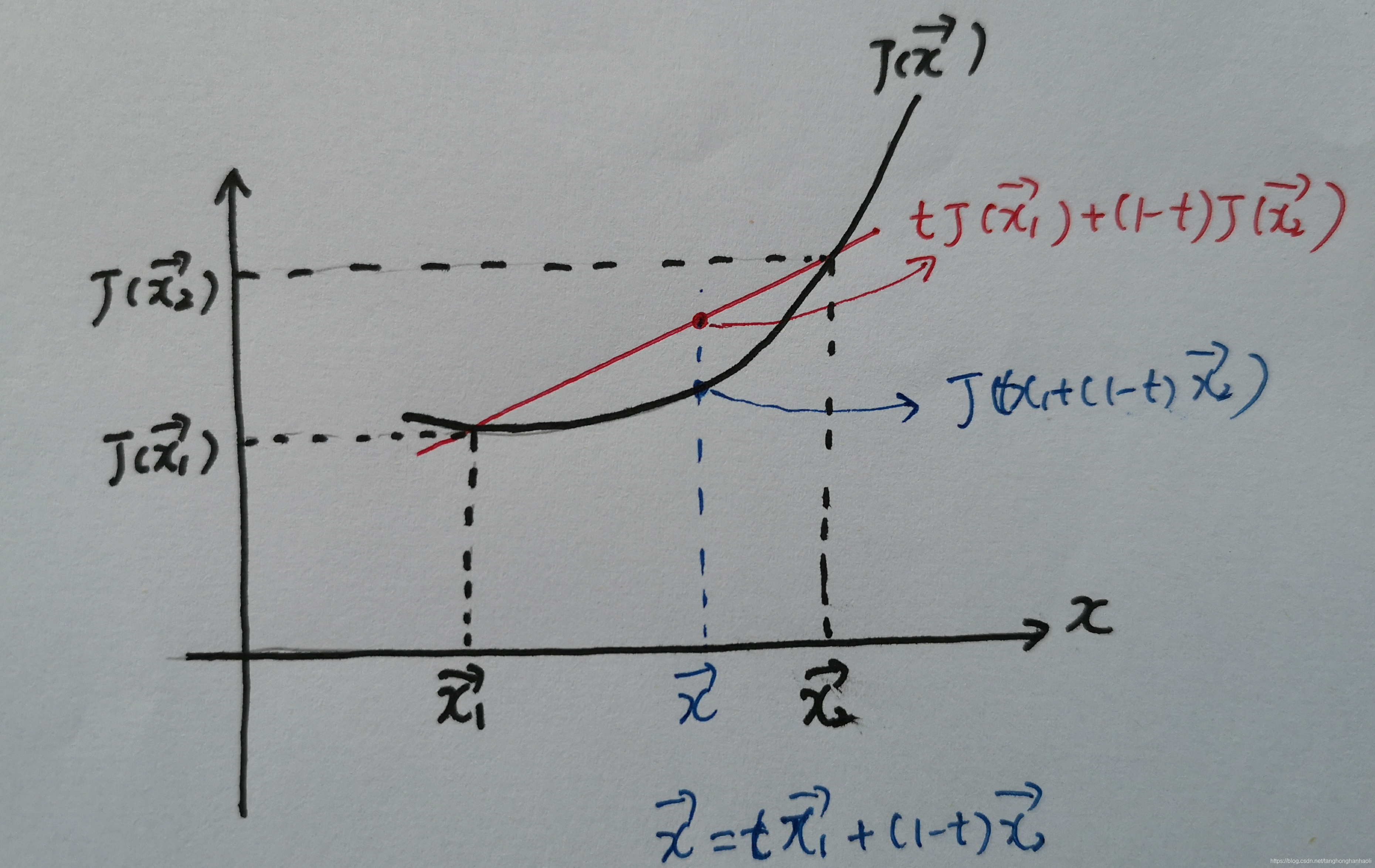
图2 凸函数的定义

  进一步，我们在《凸函数成立的一阶与二阶条件》一文中给出了凸函数成立的两个充要条件。利用二阶条件，即凸函数的Hessian阵半正定，我们知道 $\ell_2$-范数的平方是凸的，因为 $\triangledown^2||{\bf x}||_2^2=2{\bf I}$。事实上，由于对于任意的 ${\bf x}$， $\ell_2$-范数的平方的Hessian阵都是严格正定的，因此它是严格凸的，也就可以得到唯一解。

---

【参考文献】
[1] Michael Lead, Sparse and Redundant Representations, From Theory to Applications in Signal and Image Processing.

ps： $\ell$用来作为 $l$的花体很好看呀，输入\ell就OK啦。