凸函数和凸优化

前言

凸函数一直是一个头疼的事，并不是凸函数有多难，而是凸函数的定义一直是个模棱两可的概念，博主也是经常看了就忘，因此为了方便记忆，对凸函数及凸优化相关定义进行总结。
凸函数图像：
根据函数图像更加清晰地辨别凸函数的形状，然后对定义的认识才能更加的清晰。凸函数图像如下图所示：

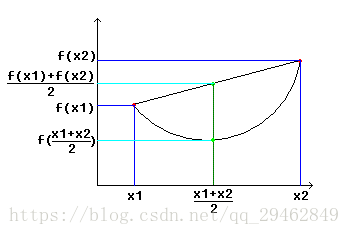
凸函数定义：
设$x_1$和$x_2$为函数f(x)定义域内的任意两个实数，且$x_1$ < t <$x_2$,恒有：

$f(\frac{x_1+x_2}{2})$ $\leq$ $\frac{f(x_1)+f(x_2)}{2}$

则称f(x) 是定义域上的凸函数。

凸函数的判定：
f(x) 在区间[a,b]上连续，在(a,b)内二阶可导，那么：
一阶判定条件: 设f(x)在凸集S上具有一阶连续偏导数，则f(x)为S上凸函数的充分必要条件是，对S中任意两点$x_1$和$x_2$，恒有：

$f(x_2)$ $\geq$ $f(x_1)$+ $\nabla$ $f(x_1)^T$( $x_2$ - $x_1$)

二阶判断条件：设f(x)在开凸集S上具有二阶连续偏导数，则f(x)为S上凸函数的充分必要条件是，f(x)的海赛矩阵在S上处半正定。

凸优化

实际建模中判断一个最优化问题是不是凸优化问题一般看以下几点：

• 目标函数f如果不是凸函数，则不是凸优化问题
• 决策变量x中包含离散变量（0-1变量或整数变量），则不是凸优化问题
• 约束条件写成g(x)\le0时，g如果不是凸函数，则不是凸优化问题

之所以要区分凸优化问题和非凸的问题原因在于凸优化问题中局部最优解同时也是全局最优解，这个特性使凸优化问题在一定意义上更易于解决，而一般的非凸最优化问题相比之下更难解决。

非凸优化问题如何转化为凸优化问题的方法：
1. 修改目标函数，使之转化为凸函数
2. 抛弃一些约束条件，使新的可行域为凸集并且包含原可行域