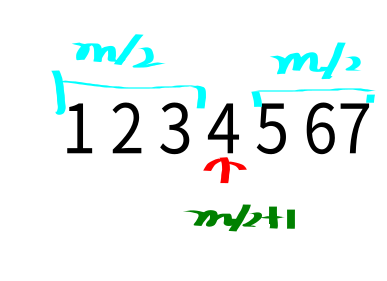序言
最近在用二分解决一些的问题的时候,
发现有一类问题-求出一个未知的序列的第K个数,这类问题对于二分边界的处理上存在不同的理解.
于是本文就这类问题进行探讨
原问题1 - poj3579
给出n个数的数组A,用这n个数每两个作差,将差值的绝对值作为一个新的数组B.这个数组有C(n,2) = n*(n-1)/2个元素.
找出B数组中的中位数.
同时n的范围为10^6,显然n^2的算法是超时和超内存的,考虑用二分来优化.
设 m = C(n,2) = n * (n-1) / 2.
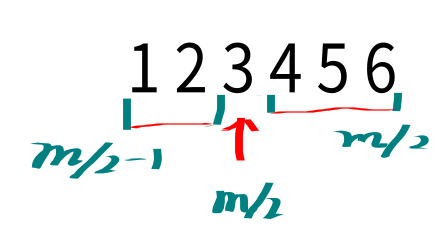
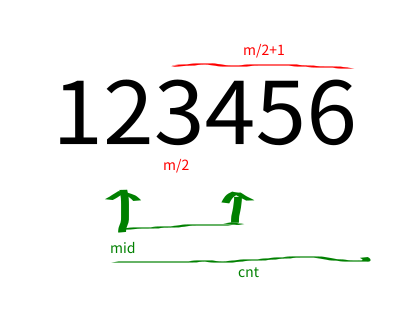
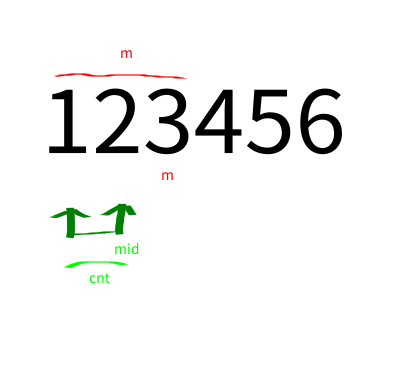
中位数定义:对于这m个数的数组B,如果m为偶数中位数为第m/2个.如果m为奇数中位数为第m/2+1个.
上图分别给出了当m为偶数和奇数的情况的中位数的情况.

我们这么做的原因就是为了分析大于,小于,等于中位数的个数有多少个
下面给出第一种解法:
通过二分枚举 mid ,mid 是我们要的中位数,对于每一个mid中位数,用lower_bound计算大于等于mid有多少个.
那么怎么计算B数组中大于等于mid的多少呢,因为B数组我们并不知道.
那么我们可以通过对A数组的二分查找,以达到计算在B数组中大于mid的个数.
因为是mid是其中两个数的差,值那么对于A[i] 来说,在B中满足大于mid的个数有 n + A - lower_bound(A+i,A+n,A[i] + mid);
读者可以自行理解下:
bool check(int mid){
ll cnt = 0,i = 0;
for(int i=0;i<n;i++) {
cnt += arr + n - lower_bound(arr+i+1,arr+n,arr[i] + mid);
}
return cnt >= (m/2+1);
}
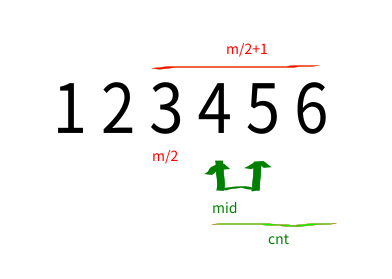
这个时候我们计算出来了大于等于mid的个数为cnt,我们看下上图,大于等于中位数的有m/2+1个,无论是奇数还是偶数
于是
当cnt < (m/2+1) 即 cnt <= m/2 时
如图:说明当前的mid一定不是中位数,则将right = mid - 1,需要向左区间去寻找(右开左闭区间) 即将当前mid直接舍去
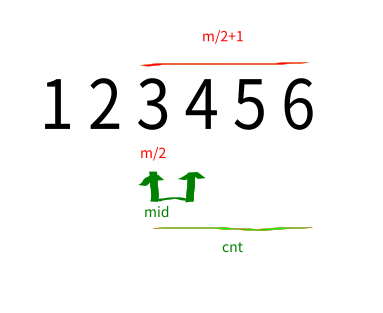
当cnt >= (m/2+1) 即 cnt > m/2 时
有两种情况. cnt == (m / 2 +1) 和 cnt >= (m / 2 + 1)
这个时候mid有可能就是中位数,而我们代码中直接将 left = mid + 1了 于是left 一定不是最优解,而right = left - 1 ,于是right一定是最优解,参照博客二分算法分析
给出代码
/**
给你n个数,然后求它们两两相减的绝对值,然后找出这些绝对值的中位数。 解题思路
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = 1e5+10;
int arr[maxn],n;
ll m;
bool check(int mid){
ll cnt = 0,i = 0;
for(int i=0;i<n;i++) {
cnt += arr + n - lower_bound(arr+i+1,arr+n,arr[i] + mid);
}
return cnt >= m/2+1;
}
int main()
{
while(~scanf("%d",&n)) {
for(int i=0;i<n;i++) scanf("%d",&arr[i]);
m = n * (n-1) / 2;
sort(arr,arr+n);
int left = 0,right = arr[n-1] - arr[0];
while(left <= right) {
int mid = (left + right) / 2;
if(check(mid)) left = mid + 1;
else right = mid - 1;
}
printf("%d\n",right);
}
}
第二种解法
对于上述问题我们可以有一个反向思路,我们也可以对于每一个可能的解mid算出小于等于他的B数组中元素的个数
于是check函数可以变成
bool check(int mid){
ll cnt = 0,i = 0;
for(int i=0;i<n;i++) {
cnt += (upper_bound(arr+i,arr+n,arr[i] + mid) - 1 - arr- i);
}
return cnt >= m;
}
有注意到这里的m 有别于上个解法的 m/2,
因为我们在计算小于等于mid的元素个数时,需要考虑奇偶了!
当m为偶数时,小于中位数的个数有 m/2-1 个.
当m为奇数时,小于中位数的个数有m/2个
于是对于m我们进行了这样的操作:
m = n * (n-1) / 2; if(m & 1) m++; m >>= 1;
偶数 m = m / 2,奇数 m = m / 2 + 1;
对于cnt < m的情况
此时的mid一定不是最优解,则需要增大mid 于是 left = mid + 1 ,left 右移
当cnt>=m时
此时的mid可能为中位数,答案,也可能不是,我们二分中直接让right = mid - 1
则right 一定不是最优解,而left 在二分结束时,left = right + 1,则left一定是最优解,参考同上
/**
给你n个数,然后求它们两两相减的绝对值,然后找出这些绝对值的中位数。 解题思路
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = 1e5+10;
int arr[maxn],n;
ll m;
bool check(int mid){
ll cnt = 0,i = 0;
for(int i=0;i<n;i++) {
cnt += (upper_bound(arr+i,arr+n,arr[i] + mid) - 1 - arr- i);
}
return cnt < m;
}
int main()
{
while(~scanf("%d",&n)) {
for(int i=0;i<n;i++) scanf("%d",&arr[i]);
m = n * (n-1) / 2;
if(m & 1) m++;
m >>= 1;
sort(arr,arr+n);
int left = 0,right = arr[n-1] - arr[0];
while(left <= right) {
int mid = (left + right) / 2;
if(check(mid)) left = mid + 1;
else right = mid - 1;
}
printf("%d\n",left);
}
}