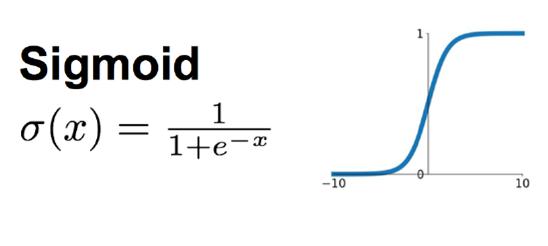逻辑斯谛回归(对数几率回归)

LR简介

逻辑斯谛回归是一种经典的线性分类方法，又被称为对数几率回归，其属于对数线性模型。

线性回归完成了数据的拟合，我们通过引入一个 $sigmoid$函数，即可在线性回归模型的基础上实现分类。

sigmoid函数定义如下
$y = \frac{1}{1 + e^{-z}}$

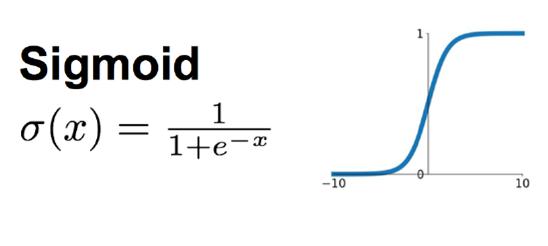
以二分类任务为例，取 $y\in \{0,1\}$，我们定义二项逻辑斯谛回归模型为如下条件概率分布：

$P(Y=1|x) = \frac{\exp(w\cdot x + b)}{1 + \exp(w\cdot x + b)}\\ P(Y=0|x) = \frac{1}{1 + \exp(w\cdot x + b)}$

一个事件的几率是指该事件发生的概率与不发生的概率的比值，如果事件发生的概率为 $p$，则该事件的几率为 $\frac{p}{1-p}$，则该事件的对数几率即为：
$\log \frac{p}{1-p}$

考虑逻辑斯谛回归模型，
$\log \frac{P(Y=1|x)}{1-P(Y=1|x)} = w\cdot x + b$

也就是说，输出 $Y=1$的对数几率是输入 $x$的线性函数。

损失函数

对于给定的训练数据集，我们采用极大似然估计法来估计模型的参数，似然函数为：
$\prod_{i=1}^N[P(y_i=1|x_i)]^{y_i}[1-P(y_i=1|x_i)]^{1-y_i}$
对数似然函数为：
$\begin{aligned} L(w,b) &= \sum_{i=1}^N[y_i\log P(y_i=1|x_i) + (1-y_i) \log (1- P(y_i=1|x_i))]\\ & = \sum_{i=1}^N[y_i\log \frac{P(y_i=1|x_i)}{1-P(y_i=1|x_i)} + \log (1-P(y_i=1|x_i)) ]\\ & = \sum_{i=1}^N[y_i(w\cdot x_i + b) - \log (1 + \exp(w\cdot x + b))] \end{aligned}$

然后对 $L(w,b)$取极大值，即可得到 $w$的估计值，通常情况下，我们将其转化为求解极小值问题.

$L(w,b) = -\sum_{i=1}^N[y_i(w\cdot x_i + b) - \log (1 + \exp(w\cdot x + b))]$
我们通常采用的方法是梯度下降法以及牛顿法.

我们用 $\theta$来替代参数.

梯度下降法的参数更新为：
$\theta \gets \theta - \alpha \frac{\partial L(\theta)}{\partial \theta}$
牛顿法的迭代形式为：
$\theta^{t+1} = \theta^{t} - (\frac{\partial^2L(\theta)}{\partial \theta^2})^{-1} \frac{\partial L(\theta)}{\partial \theta}$

采用向量形式表示则为：
$\theta^{t+1} = \theta^t - (\frac{\partial^2L(\theta)}{\partial \theta\partial\theta^T})^{-1}\frac{\partial L(\theta)}{\partial \theta}$

下面我们来推导关于 $\theta$的一阶和二阶导数：

对于代价函数采取如下形式考虑，
$L(\theta) = - [y\log \hat{y} + (1-y)\log(1-\hat{y})]$
其中， $\hat{y} = \frac{1}{1 + \exp(-z)}，z = \theta^Tx$.

根据链式求导法则
$\frac{\partial L}{\partial \theta} = \frac{\partial L}{\partial z}\frac{\partial z}{\partial \theta}$
$\frac{\partial L}{\partial z} = \frac{\partial L}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial z}$
我们有
$\frac{\partial L}{\partial \hat{y}} = \frac{\hat{y} - y}{\hat{y}(1-\hat{y})}$
$\begin{aligned} \frac{\partial \hat{y}}{\partial z} &= \Big(\frac{1}{1 + \exp(-z)}\Big)'\\ & = \frac{1}{1+\exp(-z)} - \frac{1}{\big(1 + \exp(-z)\big)^2}\\ & = \hat{y}(1-\hat{y}) \end{aligned}$
因此，我们得到了
$\frac{\partial L}{\partial z} = \frac{\partial L}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial z} = \hat{y} - y$
那么
$\begin{aligned} \frac{\partial L}{\partial \theta} &= \frac{\partial L}{\partial z}\frac{\partial z}{\partial \theta}\\ & = (\hat{y} - y)\frac{\partial z}{\partial \theta}\\ & = (\hat{y} - y)x \end{aligned}$
这里均由增广表示，因此我们得到了迭代公式
$\begin{aligned} \hat{\theta} &= \theta - \alpha\frac{\partial L}{\partial \theta} \\ & = \theta - \alpha(\hat{y}- y)x \end{aligned}$

二阶导数同理我们可以得到
$\frac{\partial^2L(\theta)}{\partial \theta\partial\theta^T} = xx^T\hat{y}(1-\hat{y})$

参考

知乎-对数几率回归
李航-统计机器学习
周志华-机器学习