逻辑回归不是回归算法，是分类算法，可以处理二元分类以及多元分类。
线性回归
线性回归的模型是求出特征向量Y和输入样本矩阵X之间的线性关系系数θ，满足Y = Xθ。此时Y是连续的，所以是回归模型。
对应n维样本数据，对应的模型是这样的：
其中θ为模型参数。
一般用均方误差作为损失函数，损失函数的代数法表示如下：
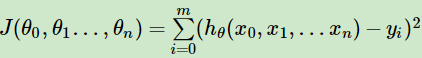
用矩阵形式表示为：
采用梯度下降法，则θ的迭代公式为：
如果采用最小二乘法，则θ为
在这里最小二乘看上去比梯度下降更简便，但是最小二乘有很多局限性：
- 需要计算
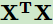的逆矩阵，有可能这个逆矩阵不存在，这时就不能使用最小二乘，但梯度下降仍然能够使用。可以通过对样本数据进行整理，去掉冗余特征，使行列式不为0，就可以继续使用最小二乘。 - 当样本特征非常大时，计算
的逆矩阵是一个非常耗时的工作，甚至不可行。此时梯度下降仍然可以使用。或者通过主成分分析降维后再最小二乘。 - 如果拟合函数不是线性的，就无法使用最小二乘，此时梯度下降仍然可以使用
线性回归的正则化
Lasso回归
线性回归的L1正则化通常称为Lasso回归，和一般线性回归的区别在于损失函数增加了一个L1正则化的项，同时有一个常数系数α来调节损失函数的均方差项和正则化项的权重，具体Lasso回归的损失函数表达式如下：
Lasso回归可以使一些特征系数变小，甚至一些绝对值较小的系数直接变为0，增强模型泛化能力。
Lasso回归的求解办法一般有坐标轴下降法和最小角回归法。但Lasso也有L1范数的缺点，它虽然是凸函数，但并不是处处可微分。
Ridge回归
线性回归的L2正则化通常称为Ridge回归。损失函数表达式如下：
Ridge回归在不抛弃任何一个特征的情况下缩小了回归系数，使得模型相对而言比较稳定，但和Lasso回归相比，会使模型的特征留的特别多，模型解释性差。
Ridge回归一般可以直接采用最小二乘法，令J(θ)的导数为0：
则最后的θ的结果：
， 其中E为单位矩阵。
也可以用梯度下降法进行表示
可以看出，在正则化系数越大的情况下，回归系数越小。当正则化系数大到一定的程度时，所有特征系数会越来越趋于0。从模型的复杂度上来解释，更小的权值代表复杂度更低，也就是说θ越小，网络复杂度越低，但是没办法让它全为0，所以没法做特征选择。
接上，上面的Y是连续的，如果想要Y是离散的，就再做一次函数转换变为g(Y)。如果使g(Y)在某个实数区间的时候为类别A，另一个实数区间的时候为类别B。就得到一个分类模型。如果类别只有两种，就是二元分类模型。
Ridge的优点包含了L2范数的优点，它是凸函数，且处处可微分。
二元逻辑回归
这个函数g一般取为sigmoid函数，形式如下：
可以看到，当z趋近正无穷，g(z)趋于1，而当z趋于负无穷时，g(z)趋于0。非常适合于分类概率模型。
另外还有一个很好的导数性质：
扯一些题外话，为什么逻辑回归叫对数几率回归，可跳过：
在使用Tensorflow时，我们可能经常会看到Logits这个东西，它其实应该分开读log it，这个it指的就是几率(Odds)，而Log it指的就是对数几率。
我们知道概率是P(A) = 发生事件A的次数 / 所有事件的次数
而几率 Odds(A) = 发生事件A的概率/不发生事件A的概率 = P(A)/1-P(A)
那对数几率就是
，这里是自然对数，它的图像是
我们用θ将P进行表示：
这不就是我们的sigmoid函数嘛？
而θ就是我们的对数几率，这就是为什么使用了sigmoid函数的逻辑回归叫做对数几率回归的原因。
顺便值得一提的是，将Logit(θ，对数几率)输入sigmoid函数时为二分类概率，输入softmax函数时（此时Logit是一维向量）便得到了多分类概率。
线性回归： Y = θX
令z = θX，则 
。其中x为样本输入，
为模型输出，理解为某一分类的概率大小。而θ为分类模型的模型参数。可以通过设置阈值，比如0.5，当比阈值大时，则y为1，反之则y为0。
的值越小，则分类为0的概率越高，反之，值越大的话，分类为1的概率越高。如果靠近临界点（阈值），则分类准确率下降。
也可以写成矩阵的模型：
，其中
为模型输出，为mx1的维度。X为样本特征矩阵，为mxn维度，θ为模型系数，为nx1向量。
二元逻辑回归的损失函数
线性回归的输出是线性的，所以可用误差平方和来定义损失函数。但是逻辑回归不是连续的，但是可以用最大似然估计法来推导出损失函数。
如果输出是0和1两类，假定输入样本x，用表示训练样本x条件下预测y = 1的概率，则
为相应样本预测y = 0的概率。
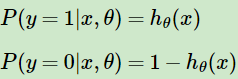
可以看出符合样本符合0-1分布（伯努力分布），将其合并则有概率分布表达式
，y为0时则是预测y = 0的概率，y为1时预测y = 1的概率。
有了概率分布表达式，则可以通过极大似然估计来求解需要的模型系数了。
极大似然估计：最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大。打个比方：一个袋子中有20个球，只有黑白两色，有放回的抽取十次，取出8个黑球和2个白球，计算袋子里有白球黑球各几个。那么我会认为我所抽出的这个样本是被抽取的事件中概率最大的。设取黑球的概率为p, p(黑球=8) = p^8*（1-p）^2,让这个值最大。极大似然法就是基于这种思想。
于是，逻辑回归的似然函数的代数表达式就为极大似然估计，我们要让以下损失函数最大：
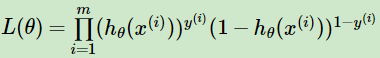，其中m为样本个数。
接着对似然函数对数化，得到对数似然损失函数表达式为：
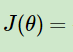
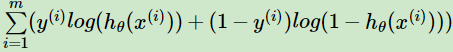
这其实正好也是二分类模型的交叉熵代价函数。
将sigmoid代入，最后得到的式子为：
，这其实就是Logistic Loss的其中一种写法，此时
。
当
，可以写成另外一种形式，
。可见当yi均为1时两个形式相等，而第一个形式当yi为0时，对应第二个形式yi为-1。
接下来，我们要找到使损失函数最大的参数θ。
通过取反，转换为找到损失函数最小时的参数θ，这个时候就可以用梯度下降法：
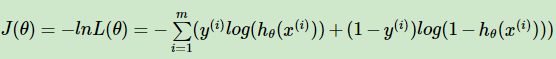
其矩阵形式为：
为什么用极大似然估计而不用最小二乘法？
实际上也可以使用最小二乘，但是最小二乘得到的权重效果比较差，因为使用最小二乘法，目标函数就是差值的平方和，是非凸的，不容易求解，容易陷入到局部最优解。
如果使用极大似然估计，目标函数就是对数似然函数，是关于(w, b)的高阶连续可导凸函数，可以方便通过一些凸优化算法求解，比如梯度下降、牛顿法等。
二元逻辑回归损失函数的优化方法
常见的有梯度下降法，坐标轴下降，牛顿法等。
这里使用梯度下降法进行推导：
二元逻辑回归正则化
常见的有l1正则化和l2正则化。
l1正则化增加了l1范数作为惩罚，超参数α作为惩罚系数，调节罚项大小。这里用矩阵形式的损失函数来表示
l1正则化一般用坐标轴下降法和最小角回归法。
l2正则化损失函数表达式为：
优化方法和普通的逻辑回归类似。
二元逻辑回归的推广：多元逻辑回归
二元逻辑回归推广到多元逻辑回归，比如总是认为某种类型为正值，其余为0值（1-vs-rest），我们可以训练k个二分类的逻辑回归分类器，第i个分类器用以区分每个样本是否可以归为第i类。
可以假设每个样本属于不同标签的概率服从于几何分布，使用多项逻辑回归（softmax regression）来进行分类
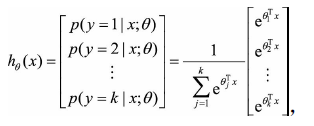
其中
为模型的参数。一般来说多项逻辑回归会有参数冗余的特点，即将
同时加减一个向量后预测结果不变。特别的，当类别数为2时：
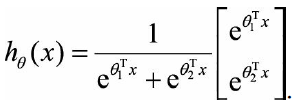
利用参数冗余的特点，将所有参数减去
，变成：
这其实就是逻辑回归的形式，可以看出二分类逻辑回归实际上是多分类逻辑回归的特例。
多元回归的推导和二元回归类似。
调参
penalty: 正则化选择参数。可选“l1”或“l2”，默认是l2的正则化。如果L2正则化还是过拟合，可以考虑L1正则化。
solver: 优化算法选择参数。默认“liblinear”，内部使用坐标轴下降法来迭代优化损失函数。“lbfgs”，拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。“newton-cg”也是牛顿法家族的一种。“sag”即随机平均梯度下降，梯度下降法的变种，和普通下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本多的时候。
multi_class：有ovr（默认）和multinomial两种选项。ovr即one-vs-rest（所有都可以看做二元逻辑回归。具体做法是，对于第K类的分类决策，我们把所有第K类的样本作为正例，除了第K类样本以外的所有样本都作为负例，然后在上面做二元逻辑回归，得到第K类的分类模型。其他类的分类模型获得以此类推），而multinomial即前面提到的many-vs-many(MvM，这里举MvM的特例one-vs-one(OvO)作讲解。如果模型有T类，我们每次在所有的T类样本里面选择两类样本出来，不妨记为T1类和T2类，把所有的输出为T1和T2的样本放在一起，把T1作为正例，T2作为负例，进行二元逻辑回归，得到模型参数。我们一共需要T(T-1)/2次分类)。如果是二元逻辑回归，ovr和multinomial并没有任何区别，区别主要在多元逻辑回归上。
class_weight: 标示分类模型中各种类型的权重，可以不输入，即不考虑权重，或者说所有类型的权重一样。“balanced”，那么类库会根据训练样本量来计算权重，某类样本量越多，则权重越低，样本量越少，则权重越高。
sample_weight: 对于样本不平衡问题，可以通过sample_weight来调节每个样本权重。如果上面两种方法都用到了，那么样本的真正权重是class_weight*sample_weight。
小结
逻辑回归是基于伯努利分布假设的概率模型，通过极大似然估计的假设，输出y=1的概率。逻辑回归也可以看做一个单层神经网络添加sigmoid函数进行分类。
逻辑回归严格来说属于广义线性模型，是非线性模型，但是在没有其他条件下只能对线性可分的数据进行分类。通过对数据进行升维（非线性映射），之后线性可分，可以使逻辑回归进行非线性分类。
逻辑回归是解决工业规模问题最流行的算法。但在工业界很少将连续值作为逻辑回归的模型的特征输入，而是将连续特征离散化为一系列0,1特征交给逻辑回归模型，这样做的优势有：
1、易于模型快速迭代
2、稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展
3、离散后的特征对异常数据有很强鲁棒性：比如大于30岁是1,300岁还是1
4、简化逻辑回归模型的作用，降低过拟合的风险
优点：
- 适合需要得到一个分类概率的场景
- 计算代价小，在时间和内存需求上相当高效。可应用于分布式数据
- 对于小噪声的鲁棒性很好，并且不会受到轻微的多重共线性的特别影响（严重多重共线性则可以使用逻辑回归结合L2正则化来解决。但是若想得到一个简约模型，L2正则化并不是最好的选择，因为它建立的模型涵盖了全部的特征）
缺点：
- 容易欠拟合，分类精度不高
- 数据特征有缺失或者特征空间很大时表现效果并不好
