线性变换和基变换

在最初理解将PCA作用于图形时，一直卡在为什么PCA获取的协方差矩阵（3*3）可以作用向量完成特定的旋转和缩放操作。后来才发现是对矩阵的了解不够透彻，在明白矩阵到底做了什么之后，才知道为什么这些博士当时能想到这么精妙的方法。在这里，最主要的是线性变换和基向量的理解。

线性变换

我们可以把线性变换理解为一种函数，我们输入一个向量，可以产生一个新的向量，

如上图所示，如果我们如果将二维中所有的点作为该函数的输入，那么所有输出的点就正好构成了一个新的二维空间，过程如下图：

那么如何确定这个变换呢，我们举一个例子，我们取 $\overrightarrow{v}=-1i+2j$ 。经过一个如下图所示的变换：

我们发现变化后的 $\overrightarrow{v}$ 正好等于-1乘变化后的i加上2乘变化后的j。即 $\overrightarrow{v}_{tran}=-1i_{tran}+2j_{tran}$ 。而且 $i_{tran}=\left ( 1,-2 \right )$ ， $j_{tran}=\left ( 3,0 \right )$ 。

$\overrightarrow{v}_{tran}=-1\begin{bmatrix} 1\\-2 \end{bmatrix}+2\begin{bmatrix} 3\\0 \end{bmatrix}=\begin{bmatrix} 1 &3 \\ -2 & 0 \end{bmatrix}\begin{bmatrix} -1\\2 \end{bmatrix}=\begin{bmatrix} 5\\2 \end{bmatrix}$ 。

我们可以发现该变换矩阵正是:

$\large I=\begin{bmatrix} 1 &3 \\ -2 & 0 \end{bmatrix}$

即由 $i_{tran}$ 和 $j_{tran}$ 为列向量构成的矩阵。到这里，我们就可以理解所有的二，三维的矩阵了，它都是将一个向量转换为另一个向量，但到这里还是不够的，我们接下来讲解一下基变换。

基变换

什么是基呢，假设2维平面内有如图所示向量：

我们称其为（3，2）向量，但是为什么是（3，2）呢，因为我们默认水平方向每格为i，竖直方向每格为j，（3，2）即3i+2j。

那如果我们想用另一种方式表示该向量呢。

我们可以定义如图所示的另一对向量b1,b2。用它们来表示刚才的（3，2）向量。结果显示该向量为（5/3，1/3）。即5/3b1+1/3b2。因此，之前提到的i，j以及现在的b1,b2就是我们的基向量。

我们会发现，b1,b2在我们通常的正交坐标系下为（2，1），（-1，1）。但在其自己的坐标系下则是（1，0），（0，1）。如下图所示：

那么这两个不同的空间的向量如何进行转换呢？

我们暂称b1,b2为基的空间为B空间。i，j的空间为A空间。比如B空间下的（-1，2）是如何转换到A空间的呢。

如上图所示因为B空间向量（-1，2）为-1b1+2b2。而b1=（2，1），b2=（-1，1），所以可得在A空间中该向量为：

$-1\begin{bmatrix} 2\\ 1 \end{bmatrix}+2\begin{bmatrix} -1\\ 1 \end{bmatrix}=\begin{bmatrix} -4\\ 1 \end{bmatrix}$

$=\begin{bmatrix} 2 &-1 \\ 1& 1 \end{bmatrix}\begin{bmatrix} -1 \\ 2\end{bmatrix}$

其中矩阵：

$I=\begin{bmatrix} 2 &-1 \\ 1& 1 \end{bmatrix}$

我们发现其列向量正好由b1，b2构成。该矩阵I也成为基变换矩阵。这里你是不是发现了，这个基变换矩阵不就是我们之前线性变换矩阵嘛。其实正是这样的，我们的线性变换矩阵都可以理解为：将空间中的一个向量转换为另一个空间中的向量。而基变换矩阵也可以理解为：将当前向量做一定的线性变换。因此线性变换矩阵和基变换矩阵则代表的是同一个东西。

那我们怎么从A空间中的向量变换为B空间中的向量呢。我们只需要把i，j转换为b1，b2的形式获得新的基变换矩阵即可。这时候我们就可以用到逆矩阵：

$I^{-1}=\begin{bmatrix} 2 &-1 \\ 1& 1 \end{bmatrix}^{-1}$

通过对刚才的I矩阵求逆，就可以把向量丛A空间转换为B空间了。

接下来我们则提一下PCA是怎么用于流体表面模拟的。

首先，我们想获取一个在A空间中的逆时针旋转90度的矩阵，如下图所示：

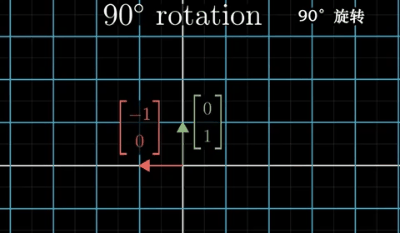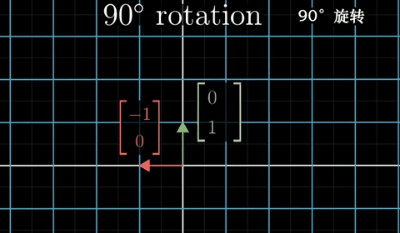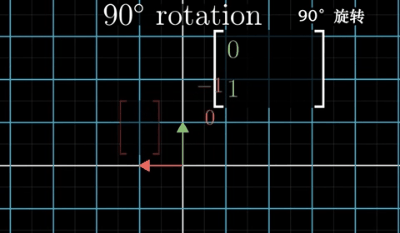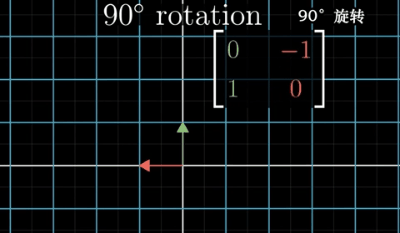
其中绿色向量是旋转后的i向量，红色向量是旋转后的j向量。我们边可以获得旋转矩阵：

$I=\begin{bmatrix} 0 &-1 \\ 1&0 \end{bmatrix}$

因此I矩阵则实现了A空间中的向量逆时针旋转90。那么我们要是在B空间下想做A空间的I变换（如下图所示变换）怎么办呢？

这时，我们不妨这样尝试，假设我们想让一个B空间的向量 $\overrightarrow{v}$ 实现上图变换，我们可以首先将该向量转换至A空间：

$\begin{bmatrix} 2 &-1 \\ 1& 1 \end{bmatrix}\overrightarrow{v}$ ，

然后将其做I矩阵变换：

$\begin{bmatrix} 0 &-1 \\ 1&0 \end{bmatrix}\begin{bmatrix} 2 &-1 \\ 1& 1 \end{bmatrix}\overrightarrow{v}$

得到便是向量 $\overrightarrow{v}$ 变换后在A空间的表示，我们然后将其变换为B空间：

$\begin{bmatrix} 2 &-1 \\ 1& 1 \end{bmatrix}^{-1}\begin{bmatrix} 0 &-1 \\ 1&0 \end{bmatrix}\begin{bmatrix} 2 &-1 \\ 1& 1 \end{bmatrix}\overrightarrow{v}$

到这里，我们的 $\overrightarrow{v}$ 向量便是经过A空间I变换的B空间向量了。了解到这里，我们之后就能明白为什么通过PCA获取的矩阵能使流体表面平滑了。

0小龙虾0

发布了22 篇原创文章 · 获赞 22 · 访问量 2584

私信关注