机器学习——多变量线性回归

1.多功能

在单变量线性回归问题中，我们只有一个特征量x；比如经典的房价预测问题，当时我们只有一个特征量：即房屋的面积x，曾设预测函数为： $h(θ) = θ_0 + θ_1x$
但是，在真实情况下，房子的价值并不仅仅只受面积的影响，还受到其他的许多因素的影响：比如说房屋的楼层数、卧室的数量、交通的便利指数、房屋的使用时间等等共同决定，因此，引入多变量就非常具有实际意义。

下面介绍我们的符号约定（也是吴恩达老师未来会在课程中使用的符号）：
我们令： $x^{(i)}$表示第i个样本；令 $x_j$表示每一个样本所具有的特征， $x^{(i)}_j$表示第i个样本的第j个特征量。例如： $x^{(2)} = \begin{bmatrix}x_1 \\ x_2\\ \vdots \\x_n\end{bmatrix}$
就表示第二个样本所具有的全部特征量

有了多变量，那么我们的预测函数就变为了： $h_θ(x) = θ_0 + θ_1x_1 + θ_2x_2 + \cdots + θ_nx_n$
这里，为了后面的方便，我们令 $x_0^{(i)}$ = 1（即增加一个为1的第0个特征）

那么，对于某一个样本而言，其向量形式就变成了这样： $\vec{X} = \begin{bmatrix}x_0 \\ x_1 \\ x_2\\ \vdots \\x_n\end{bmatrix}$
n+1维
同理，θ的向量形式就变成了： $\vec{θ} = \begin{bmatrix}θ_0 \\ θ_1 \\ θ_2\\ \vdots \\θ_n\end{bmatrix}$
也是n+1维
那么，我们来看看 $h_θ(x) = θ_0 + θ_1x_1 + θ_2x_2 + \cdots + θ_nx_n$能否换成下面的形式：
$h_θ(x) = \vec{θ}^TX$（用矩阵乘法的形式表达，非常简洁）
$θ^TX = [θ_0, θ_1, \cdots, θ_n] \begin{bmatrix}x_0 \\ x_1 \\ x_2\\ \vdots \\x_n\end{bmatrix}$

2.多元梯度下降法

还记得我们的损失函数：cost: $J(θ_0, θ_1, \cdots, θ_n) = \frac{1}{2m}\sum_{i = 1}^m(h_θ(x^{(i)} - y^{(i)})^2$
当然，我们现在可以用: $J(\vec{θ})$来代替 $J(θ_0, θ_1, \cdots, θ_n)$

那么，我们的梯度下降法是这样的： $θ_j := θ_j - α\frac{\partial{J(\vec{θ})}}{\partial{θ_j}}$
这里的求导并不复杂，我就简单介绍一下步骤：

1. 计算： $\frac{\partial{J(\vec{θ})}}{\partial{h_θ(x^{(i)})}}$； $\frac{\partial{J(\vec{θ})}}{\partial{h_θ(x^{(i)})}} = \frac{1}{m} \sum_{i = 1}^m(h_θ(x^{(i)} - y^{(i)})$
2. 计算： $\frac{\partial{h_θ(x^{(i)})}}{\partial{θ_j}}$,由上面的预测函数： $h_θ(x) = θ_0 + θ_1x_1 + θ_2x_2 + \cdots + θ_nx_n$可知： $\frac{\partial{h_θ(x^{(i)})}}{\partial{θ_j}} = x_j$
   因此， $\frac{\partial{J(\vec{θ})}}{\partial{θ_j}} = \frac{1}{m} \sum_{i = 1}^m(h_θ(x^{(i)} - y^{(i)})x_j$

2.1.多元梯度下降法演练Ⅰ- 特征缩放

我们想要不同的特征的取值在相近的范围内。这样做的目的是使得梯度下降法能够更快地收敛
比如在房价预测的例子中：
如果有两个特征：1.房子的面积；2.卧室的数量
如果第一个特征的取值范围在0~ 2000，而第二个特征的取值范围只是0~5,那么，我们我们的 $θ_1,θ_2$的等值曲线可以就非常曲折瘦高。这样梯度下降法可能会花上很长的时间去逼近最优解

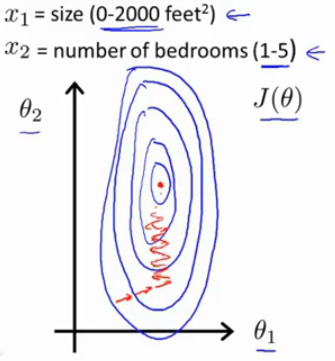
但是，如果我们进行一下特征缩放，也就是将这两个取值范围相差很大的特征通过一些处理，使得它们的取值范围接近，比如我们可以这样做： $x_1 = \frac{size}{2000}\\ x_2 = \frac{number \space of \space bedroom}{5}$
那么，此时 $x_1$的取值范围被缩放成了[0,1]， $x_2$的取值范围也被缩放成了[0,1]，那么 $θ_1，θ_2$的等值曲线就变成了长和宽都接近的近似的同心圆，这样我们梯度下降可以快速收敛

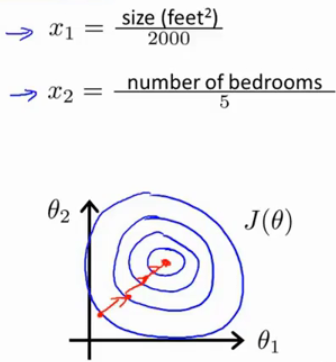
我们喜欢将特征缩放到-1和1的范围内，对于其他不同的x，可能需要通过乘以或除以不同的数，让他们缩放到合适的区间，当然，不一定非要等于-1和1，接近就行

扫描二维码关注公众号，回复： 8791142 查看本文章

下面介绍一下特征缩放的常用方法：均值归一化
均值归一化：即如果特征是 $x_j$，我们就用 $\frac{x_j - μ_j}{S_i}$去替换 $x_j$，让新的 $x_j$的均值为0，下面解释一下这些符号的意思：
$μ_j$：是所有样本中 $x_j$的均值
$S_j$：是特征值 $x_j$的取值范围[min, max]的长度，即max - min

其实，在实际编程中，还有几个常用的缩放范围，比如[-3,+3],[- $\frac{1}{3}, +\frac{1}{3}$]…

2.2.多元梯度下降法Ⅱ - 学习率α

在我们梯度下降中变量更新的式子中，用到了学习率α（我们需要在一开始自己设定）

通常，我们会画出 $J(\vec{θ})$的曲线图，通过曲线的变化情况来判断我们的算法有没有正常工作，一般来讲， $J(\vec{θ})$的值会随着迭代次数慢慢下降，但是我们也可能会遇到下面的情况：

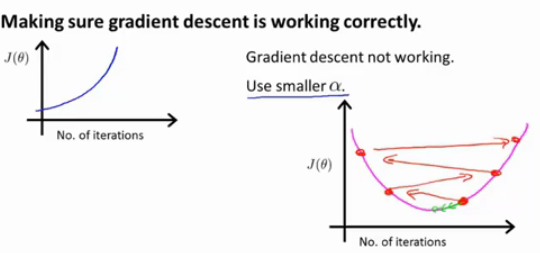
也就是我们的损失函数的曲线不降反升：这时我们可以尝试换用更小的学习率
为什么呢？

假设我们的cost function是二次函数，我们需要找到最小值，假设一开始我们的点在最小值右侧附近，如果学习率过大，那么该点可能在下一次迭代中会冲过最小值点，到达右侧上端，在后面的迭代中又会继续冲到更上面，这就导致cost值越来越大

还有一种情况，就是cost值一会降，一会升，一会又降，一会又升…
这种情况下，也是尝试降低学习率，但在吴恩老师的课程中没有给出证明，因此，用下面的图总结一下：

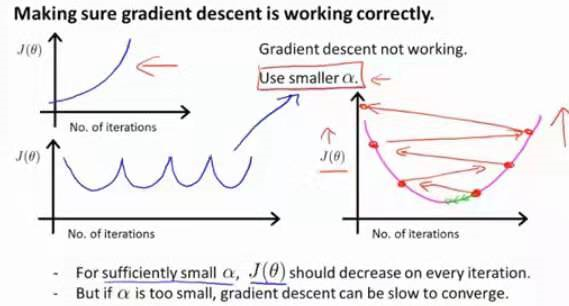
事实证明：如果α取得足够小，那么每一次的cost应该都会下降，但是我们也不希望α特别小，否则你的算法将收敛得很慢

3.特征和多项式回归

4. 正规方程（区别于迭代方法的直接解法）

首先，如果我们的cost function： $J(\vec{θ})$ = $aθ^2 + bθ + c$
那么，我们知道要找最小值就是对 $θ$求导，然后让导数置零

对于复杂的cost function：
$J(θ_0, θ_1, \cdots, θ_n) = \frac{1}{2m}\sum_{i = 1}^m(h_θ(x^{(i)} - y^{(i)})^2$
我们也可以分别对不同的 $θ$求偏导，然后令导数等于0，迭代计算不同 $θ$的最优值

但是，今天所介绍的正规化方法，是对于多变量线性回归的快捷解法：

首先，我们构造设计矩阵：每一行包含一个不同的样本。每一列对应于不同的特征。
原本以恶搞样本的矩阵是这样的： $x = \begin{bmatrix}x_0^{(i0}\\x_1^{(i)}\\ \vdots \\ x_n^{(i)}\end{bmatrix}$
那么，全体样本的X矩阵就是这样的：
$\vec{X} = \begin{bmatrix}——& (x^{(1)})^T & —— \\ ——& (x^{(2)})^T & —— \\ & \vdots \\——& (x^{(m)})^T & ——\end{bmatrix}$
这和我们之前所学习的神经网络的输入矩阵有一点不同

然后，对于y，我们这样构造： $\vec{Y} = \begin{bmatrix}y^{(1)}\\y^{(2)}\\ \vdots \\ y^{(i)}\end{bmatrix}$

那么， $θ$的最优解可以通过下面的式子一步到位地求出来： $\vec{θ} = (\vec{X}^T\vec{X})^{-1}\vec{X}^T\vec{Y}$

下面介绍特征方程和梯度下降各自的优缺点：
Gradient Descent：
优点：即使特征数n非常大的时候也非常有效
缺点：需要自己选择学习率；需要很多次的迭代
Normal Equation：
优点：不需要选择学习率；不需要多次迭代
缺点：需要计算 $(\vec{X}^T\vec{X})^{-1}$，所以当n很大的时候非常浪费时间
说明：

1. 正规方程只适用于线性回归，而梯度下降适用于大部分场合
2. 如果使用了正规方程，那么可以不需要做特征缩放
3. 如果特征数n是几百个（或者上千个），选择特征方程；如果特征数非常大比如 $10^6$…，那么选择梯度下降法