机器学习（三）——多变量线性回归

一、前言：

二、模型描述：

1.Hypothesis：

一、前言：

吴恩达第五章多线性变量回归笔记（所有例子均来自吴恩达机器学习视频课的内容）
在所有公式中，n为特征个数，m为样本数量

二、模型描述：

与前面单变量线性回归类似，只是input值的个数，即特征的个数从一个变成了多个。

在上个单变量线性回归中，只采用了一个特征，房子尺寸，这里我们多添加了房间个数、楼层数以及房子的"年龄"。分别将这三个变量设为x1,x2,x3,x4。结果设为y。

1.Hypothesis：

$H_\Theta (x)=\Theta _0+\Theta _1x_1+\Theta _2x_2+....+\Theta _nx_n$

用矩阵表示：

由此得：

$\large H_\Theta (x)=\Theta ^\tau x$

2.Cost Function:

$\large J(\Theta _0,\Theta _1)=\frac{1}{2m}\sum_{i=1}^m (h\Theta (x^{i})-y^{i})$

三、多元梯度下降法

多元线性回归的代价函数和单变量的回归的代价函数是一样的,都是原参数减去学习率与原参数在代价函数上的偏导的乘积：

repeat until convergence{

$\large \Theta _j:=\Theta _j-\alpha \frac{\partial J(\Theta_0,\cdots,\Theta _n )}{\partial \Theta _j}$

}

(全部同时更新)

1.特征放缩

虽然多元线性回归的梯度下降方法和单变量回归没有太大的差别，但是多元线性回归涉及到单变量回归没有的问题，就是多个特征值的取值差别过大，导致模型很难拟合。因此需要运用特征缩放的方法对数据进行预处理。

特征缩放其实很简单，比如我们的两个变量房屋的面积和房间数。房屋的面积的范围在0-2000英寸，而我们的房间数在1-5间，这两个特征值就相差过大，导致梯度下降的困难。

只需要把房屋面积除以2000，房间数除以5，这样两个特征值的范围就在0-1之间，梯度下降就更加容易。

通常放缩得范围有如下几种：

-1 ~ 1
-3 ~ 3
-1/3 ~ 1/3

2.学习率α的选择：

可以绘制出梯度下降迭代的次数和代价函数值的关系图，来判断函数是否收敛，从而判断这个学习率是否合适。

若学习率合适，则图像如下图所示

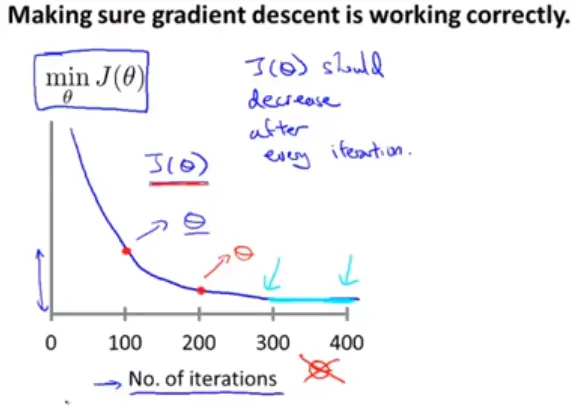
假如图像函数曲线随着迭代次数增加而上升，说明我们的学习率过大。

假如曲线是忽上忽下，则说明我们的学习率偏小。

根据图像我们就可以找到方向修改我们的学习率到合适的大小。通常学习率的改变方式是每十倍取值，比如0.001偏小了，则采取0.01，再偏小再取0.1。也可以采取每三倍的取值。

四、特征与多项式回归

很多时候采取的数据集的数据分布不是直线型的，可能是曲线，也可能是其他图形，此时就需要拟合非直线型的函数

比如这个房屋面积与价格的数据，我们可以看出来像一条抛物线，可以用二次模型去拟合。但是由一定数学知识就可以知道，当size超过一定值时，Price会随着Size的增大而减小，显然是与实际情况不相符的。此时便需要采取更加合理的三次模型。

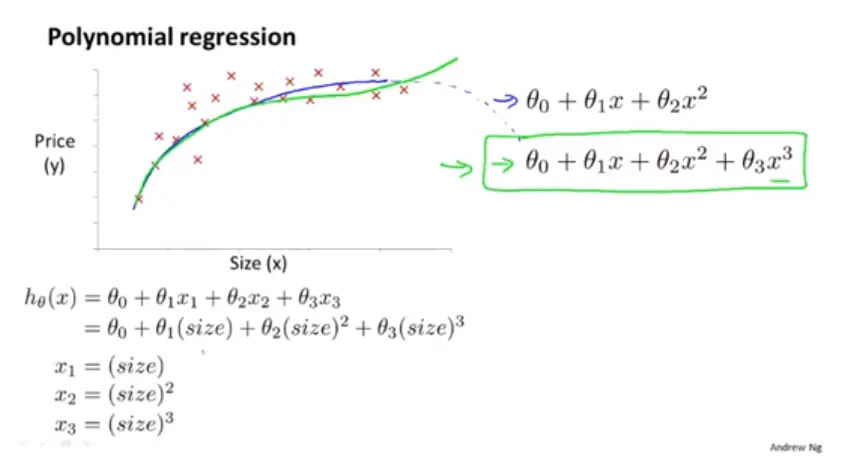
此时函数就转化成用x1,x2,x3建立的模型。拟合度更高。

采取多次模型，特征放缩更为重要！

五、正规方程（区别于梯度下降法）

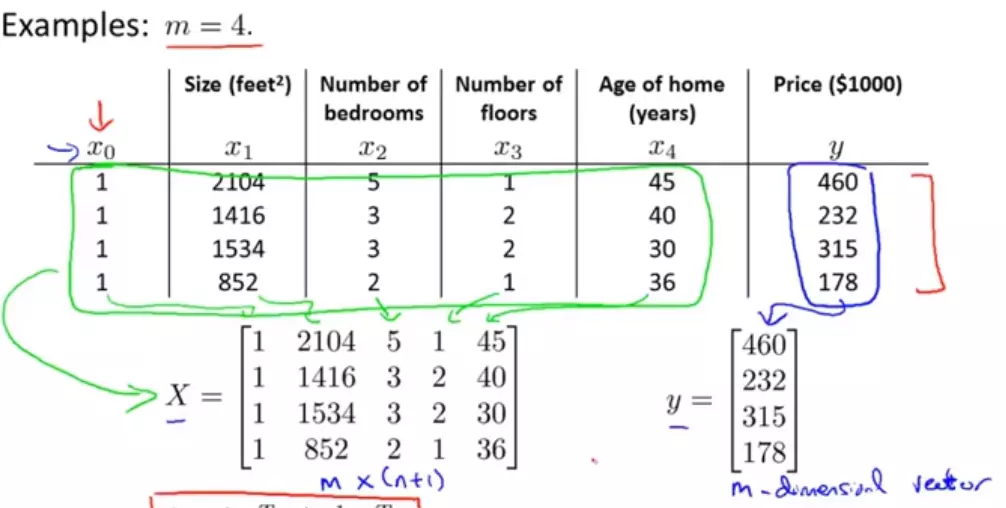
在得到矩阵X与矩阵y时，可以通过一下公式的到最佳θ值（数学原理视频也没解释我也不懂）

$\large \Theta =(X^TX)^{-1}X^{T}y$

用这种方法不需要进行特征缩放

六、梯度下降法与正规方程法的比较

梯度下降法	正规方程法
需要选择学习率α（缺点）	不需要选择学习率α（优点）
需要迭代（缺点）	不需要迭代（缺点）
当特征数n非常大时，效率高（优点）	当特征数n非常大时，效率低（优点）