机器学习最好的公开课——多变量线性回归

本文为目前机器学习最好公开课——吴恩达机器学习的学习总结，我们讲解多变量线性回归模型。

多变量

还记得我们在一元线性回归模型中房屋价格预测的例子吗？在这里我们对这个例子继续进行扩展，我们将影响房屋价格的特征变为了 4 个。

我们用 $x_1,x_2,x_3,x_4$ 分别表示 4 个特征，然后进行一些定义方便后面的叙述：

• $n$：表示特征数量，这里为 4；
• $x^{(i)}$：表示第 $i$ 个训练样本的输入值，即一个特征向量；
• $x^{(i)}_j$：表示第 $i$ 个训练样本的第 $j$ 个特征。

例如 $x^{(2)}$ 表示 $\left[ \begin{matrix} 1416\\ 3 \\ 2 \\ 40 \end{matrix} \right]$， $x^{(2)}_2$ 表示 3。

现在，我们重写假设函数。因为输入涉及了多个特征，因此我们需要增加多个参数。因此多变量线性回归的假设函数为：
$h_\theta(x)=\theta_0+\theta_1x_1+…+\theta_nx_n$
这里为了方便起见，我们定义 $x_0=1$，从而将上式写为内积的形式：
$h_\theta(x)=\theta_0x_0+\theta_1x_1+…+\theta_nx_n=\left[ \begin{matrix} \theta_0 & \theta_1 & … & \theta_n\\ \end{matrix} \right]·\left[ \begin{matrix} x_0\\ x_1 \\ … \\ x_n \end{matrix} \right]=\vec{\theta^T}·\vec{x}$
其中 $\vec{\theta}=\left[ \begin{matrix} \theta_0\\ \theta_1 \\ … \\ \theta_n \end{matrix} \right],\vec{x}=\left[ \begin{matrix} x_0\\ x_1 \\ … \\ x_n \end{matrix} \right]$。

于是，我们便可以用更紧凑的方式表示假设函数了。

多变量的梯度下降

首先简单回顾一下我们前面讲的单变量线性回归模型，就能更好的理解这部分的内容了。

多变量线性回归的假设函数为：
$h_\theta(x)=\vec{\theta^T}·\vec{x}=\theta_0x_0+\theta_1x_1+…+\theta_nx_n$
我们将参数表示为 $\vec{\theta}$ 的形式。则代价函数为：
$J(\vec{\theta})=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2$
于是对应梯度下降为：
$\theta_j:=\theta_j-α\frac{\partial}{\partial\theta_j}J(\vec{\theta})$
我们对导数项进行求解得到：
$\theta_j:=\theta_j-α\frac{1}{m}\sum_{i=1}^m(h_θ(x^{(i)})-y^{(i)})^2x^{(i)}_j$
当 $j=0$ 时， $x^{(i)}_0$ 定义为 0，与一元梯度下降的形式相同。

接下来我们将介绍一些梯度下降算法的使用技巧。

梯度下降实践 I：特征缩放

一个机器学习问题有多个特征，若能保证多个特征的取指在相近的范围内，梯度下降法可以更快的收敛。

我们首先看一个例子，通过这个例子对特征缩放进行介绍。

为了便于讨论，我们仍在这里令 $\theta_0=0$。我们直接画出代价函数的等高线图：

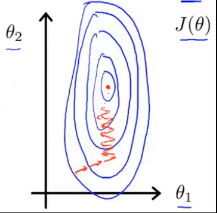
我们画出的图像是又高又瘦的椭圆，在这种情况下算法的收敛速度会很慢，并且可能来回波动才能达到最终结果。解决这个问题的一种方法是进行特征缩放。如果我们定义 $x_1=\frac{size}{2000},x_2=\frac{\#bednums}{5}$（其中 # 表示数量），则对应代价函数的等高线图为：

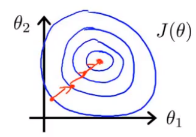
可见图像为一个近似的圆，且近似满足 $0\le x_1\le 1,0\le x_2\le 1$，可以从数学上证明，算法在这种情况下比上面那种情况能更快的收敛。其实我们只需要将特征的取值近似约束在 -1 到 1 之间即可，我们可以对近似稍作规定，如果取值范围大于 -3 到 3 或者小于 $-\frac{1}{3}$ 到 $\frac{1}{3}$，那我们就需要注意了。

在特征缩放中，我们有时还会进行均值归一化，将 $x_i$ 替代为 $x_i-μ_i$（ $μ_i$ 表示均值），使得 $x_i$ 为 0，当然无需将其运用到 $x_0$ 中。于是我们可以定义 $x_1=\frac{size-1000}{2000},x_2=\frac{\#bedrooms-2}{5}$，此时我们得到的特征大致范围为 -0.5 到 0.5。通常，我们会进行变换 $x_i \leftarrow \frac{x_i-μ_i}{S_i} $，其中 $S_i$ 可以为最大值减去最小值，也可以是变量的标准差。

通过使用这个简单的方法，我们可以加快梯度下降的收敛速度，收敛所需的迭代次数将会更少。

梯度下降实践 II：学习率

这部分我们讲解梯度下降算法如何进行 Debug 以及如何选择合适的学习率 $α$。

通常在调试的时候，我们可以画出 $J(\theta)$ 与迭代次数的关系图，其中 $J(\theta)$ 表示当前迭代次数对应的参数值的代价函数。这种方法有 3 点好处。

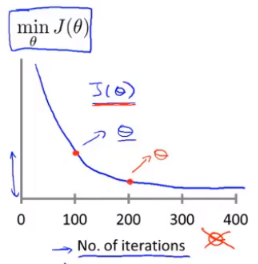
1. 判断算法收敛。

   我们可以看到迭代次数为 300 和 400 之间的线近似平坦，因此我们也可以通过观察曲线来判断算法是否已经收敛。其实我们还可以通过自动收敛测试来判断收敛，例如设定阈值 $\epsilon$，当代价函数值小于阈值时，则认为已经收敛，但是使用这种方法时阈值 $\epsilon$ 很难设定，更便捷的方法还是观察图像。

2. 判断算法是否正常运行

   算法正常运行时的函数图像如上图所示，如果出现了下图中代价函数递增或代价函数值上下波动的情况，则算法可能出错了。

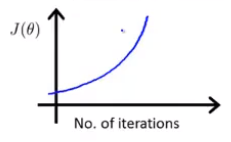
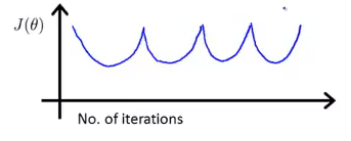
3. 选择合适的学习率

   数学家已经证明，当学习率 $α$ 很小的时候，梯度下降算法一定会收敛。因此如果出现了上图中的两种情况，很可能是学习率选的太大。下图中的红色线表示选择了过大的学习率，蓝色线表示选择了过小的学习率。

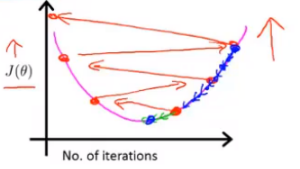
当我们选择学习率时，我们通常可以选择 …, 0.001, 0.01, 0.1, 1, … 这种相差 10 倍的取值，或者在每 10 倍中增加一个 3 倍的取值： …, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, …

特征与多项式回归

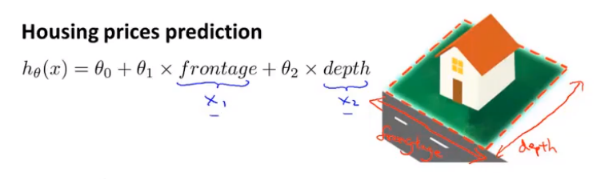
其实，特征的选择也有一定的技巧。我们看一个例子。还是一个房价预测的问题，此时我们得到的变量是房屋的长和宽，但我们可以不用长和宽作为我们的特征 $x_1,x_2$，我们可以定义一个新的特征 $Area=x_1\times x_2$ 表示房屋的面积，影响我们房屋价格的因素应该是面积，而不是特定的长和宽。因此我们需要知道的是，我们可以巧妙地选择特征从而获得更好的模型。

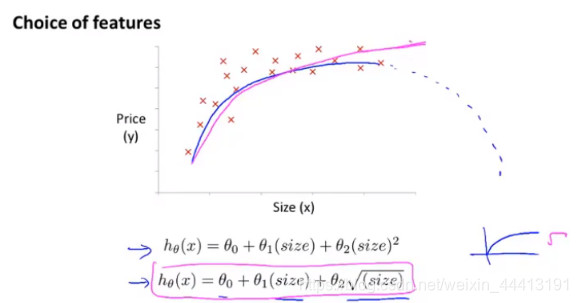
多项式回归是一个与特征选择思想类似的一个方法。如下图是我们得到的面积和房屋价格关系的数据集，显然它不是线性的，但如果我们用二次函数拟合（蓝色曲线），房屋价格随着面积的增加反而会下降，这显然不合理，因此我们可能会考虑选择三次函数进行拟合（绿色曲线），显然得到更好的拟合结果。于是，我们需要对我们的线性回归模型做一些小的修改：

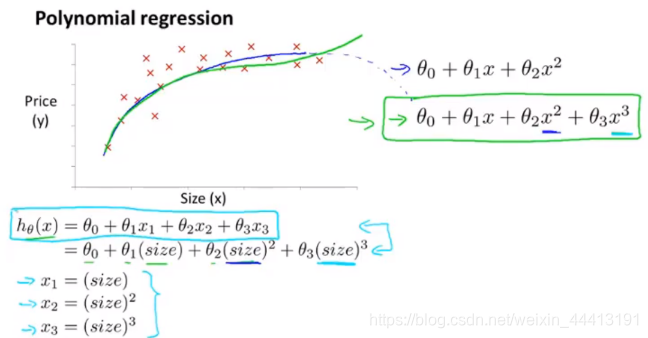
这样一来，我们就能够将多项式函数转换为线性模型进行求解。我们需要注意的是，如果我们采用了多项式回归的方法，我们的特征缩放操作就变得尤为重要，因为面积的二次方和三次方会相差很多个数量级，我们需要对特征进行缩放从而让特征之间可比。

再说一点，我们也可以通过观察数据集从而选择好的拟合函数。在房屋价格预测的例子中，我们预期得到的拟合曲线是面积足够大时，图像的斜率会变小，这时根号函数相对于二次和三次函数是一种更好的选择。

正规方程

在一些线性回归问题中，正规方程会给我们一个求得最优值的更好的方法。当我们使用梯度下降算法时，我们需要很多次迭代才能找到最优解，但正规方程可以一次性地直接求得最优解。

我们令 $x^{(i)}=\left[ \begin{matrix} x_0^{(i)}\\ x_1^{(i)} \\ … \\ x_n^{(i)} \end{matrix} \right]∈R^{n+1},X=\left[ \begin{matrix} (x^{(1)})^T\\ (x^{(2)})^T \\ … \\ (x^{(m)})^T \end{matrix} \right],y=\left[ \begin{matrix} y^{(1)}\\ y^{(2)} \\ … \\ y^{(m)} \end{matrix} \right]$

这里我们不加证明的直接给出正规方程求解最优解的公式：
$\theta=(X^TX)^{-1}X^Ty$
在 Octave 中，我们只需要一行代码解决：

pinv(x'*x)*x'*y

并且在正规方程中，我们无需进行特征缩放。

那么我们应该如何选择该使用梯度下降法和正规方程法呢？在这里我们对两个方法的特点用一个表格进行总结，以作参考。

	梯度下降法	正规方程法
优点	在 $n$ 很大时能够正常运行	无需选择学习率 $α$ 一次计算即可得到结果
缺点	需要选择学习率 $α$ 需要多次迭代	在 $n$ 很大时， $(X^TX)^{-1}$ 是求解 $n\times n$ 矩阵的逆，时间复杂度为 $O(n^3)$

从表格中可以看出，两种方法选择的决定性依据就是 $n$ 的大小。一般当 $n<10000$ 时，我们考虑使用正规方程法；然而当 $n>10000$ 时，我们可能就需要考虑使用梯度下降法了。

在我们后面学习一些复杂的算法时，正规方程法在很多情况下无法求解，这时我们仍需要使用梯度下降法。但对于这个特定的线性回归模型，正规方程法则是梯度下降法的一种很好的替代方案。

正规方程与不可逆性

在回顾线性代数的文章中，我们提到了一种不可逆的矩阵，称为奇异矩阵或退化矩阵。我们思考一个问题，如果在正规方程法中求解 $(X^TX)^{-1}$ 时， $X^TX$ 的是一个奇异矩阵，我们该怎么办呢？

其实我们大可不必担心这种情况，因为这种情况一般不会发生，并且我们在 Octave 中使用的 pinv 实际上是求解伪逆（inv 用来求逆），从数学上可以证明 pinv 求解得到的 $\theta$ 是一个正确的值。

发生这种情况的原因有 2 种。

一是存在冗余特征。例如 $x_1,x_2$ 分别表示以英尺和平方米为单位的房屋面积，此时 $x_1,x_2$ 间存在线性关系 $x_1=(3.28)^2x_2$，此时我们只需要删除冗余特征就可以解决问题；

另一个原因是特征太多（ $m≤n$）。例如 $n=100$，而 $m=10$，相对于 100 个特征来说，10 个样本过于少了。我们可以删除一些无用的或相关性小的特征，也可以进行正则化减少特征数量。关于正则化的知识我们后面将会介绍。

至此，我们有关线性回归的相关知识就介绍到这里，这个简单的模型已经能够很好的解决我们平时遇到的许多问题了，更为复杂的算法我们将在后续进行介绍。