逻辑回归

从分类问题思考:线性回归与逻辑回归

分类问题
0:Negative class
1:Positive Class
二分类问题开始
将已知数据分类 0 1
采用算法 线性回归
假设函数 hx = theta0 + theta1*x1 + ... + thetaN * xN
设置阈值---什么情况下属于1类 or 0类
        > 0.5 1
        < 0.5 0
所有的点 
对于分类问题应用线性回归并不是好办法

还有一个有趣的事情:
classification： 0 or 1
but 假设函数可以 大于1 or 小于0

接下来使用逻辑回归算法进行分类
logistic regression 逻辑回归
逻辑回归:实际上是一种分类算法

机器学习三要素模型策略算法

逻辑回归假设函数 – 模型

logistic regression model
目标:
    将假设函数值限定在[0,1]之中
    如果 >= 0.5 属于 1类
    反之 属于0类
    want 0< hx < 1

逻辑回归的假设函数的表达式是什么?
逻辑回归的假设函数与线性回归的假设函数不同 
带入了越阶函数 sigmoid function
线性回归hx = theta^T*x
逻辑回归hx = g(theta^T*x)

逻辑回归 – 从线性回归假设函数逐步优化

假设函数 : $h\theta(x) = \theta^T x$ 逻辑回归的目标是分类输出 0 or 1 引入 sigmoid function 即: $h\theta(x) = g(\theta^T x)$ $g(z) = \frac {1}{1+\rho^(-z)}$ 模型的解释对于新输入样本x的y等于1的概率的估计值即为: $g(z) = \frac {1}{1+\rho^(-\theta^T x)}$

总结: 
    逻辑回归的假设函数是什么
    定义逻辑回归的假设函数的公式是什么

逻辑回归模型假设函数的推导
这里写图片描述
如何从解释该模型模型转化的思路

决策边界

决策边界：假设函数在计算什么
目标:预测分类问题
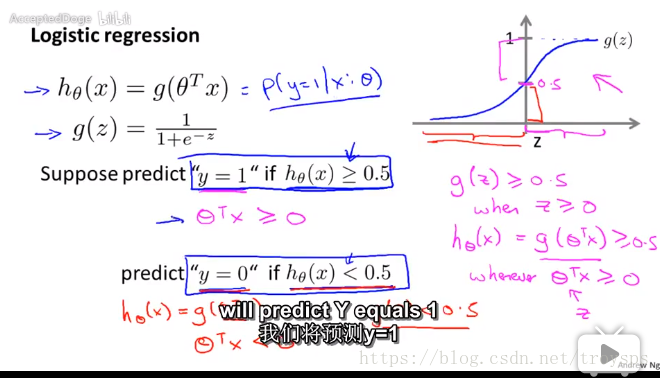
suppose predict “y=1” if $h\theta(x) >= 0.5$
即 $\theta^T x >= 0$
“y=0” if $h\theta(x) < 0.5$
即 $\theta^T x < 0$

$h\theta(x) = g(\theta^T x) = p(y=1|x;\theta)$
$g(z) = \frac{1}{1+e^{-z}}$

什么是决策边界
决策边界时假设函数的一个属性包含 $\theta$ 数据集分平面
一旦确定 $\theta$ 参数决策边界就确定

决策边界可以是线性也可以是非线性
并不是用训练集来训练$\theta$ 而是拟合$\theta$

总结与思考: 什么范围内的假设函数可以选择
如何确定决策边界

非线性的决策边界
这里写图片描述

逻辑回归的代价函数

traning set
${(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), ..., (x^{(m)}, y^{(m)})}$
m examples x 属于 [x_0, x_1,…,x_n].T
$R^{n+1} x_0=1 y属于{0,1}$
逻辑回归的假设函数为: $h\theta(x) = \frac{1}{1+e^{-z}} = \frac{1}{1+e^{-\theta^T x}}$
线性回归的代价函数
linear regression cost function :
$J(\theta) = \frac{1}{m}\sum \limits_{i=1}^{m} \frac{1}{2}(h\theta(x^{(i)}) - y^{(i)})^2$
可以推导为: $Cost(h\theta(x^{(i)}),y^{(i)}) = \frac{1}{2}(h\theta(x^{(i)})-y^{(i)})^2$
即为: $Cost(h\theta(x), y) = \frac{1}{2}(h\theta(x) - y)^2$

由于 $h\theta(x)$ 为复杂线性函数开平方推导会造成非凸函数以及局部优化

因此期望是凸函数
可得逻辑回归的代价函数为
$Cost(h\theta(x), y) = -log(h\theta(x)) if y = 1$
$Cost(h\theta(x), y) = -log(1-h\theta(x)) if y = 0$

特性:当y=1时 if $h\theta(x)=1$ cost=0
else: $h\theta(x)=0$ 代价函数无穷大

当y=0时 if $h\theta(x)=1$ 代价函数无穷大
else cost=0
代价函数作为惩罚系数

逻辑回归代价函数推导1
这里写图片描述
逻辑回归代价函数推导2 凸函数与非凸函数

逻辑回归代价函数推导3

Simplified cost function and gradient descent

化简代价函数及梯度下降法

——问题如何使用梯度下降法拟合函数
——线性回归和逻辑回归是一个梯度下降算法么
——如何检测梯度下降确保他是收敛的

将代价函数再化简
$J(\theta) = \frac{1}{m} \sum\limits_{i=1}^{1}Cost(h\theta(x^{(i)}), y^{(i)})$
$Cost(h\theta(x), y) = -log(h\theta(x)) if y = 1$
$Cost(h\theta(x), y) = -log(1-h\theta(x)) if y = 0$

Note! y=0 or 1 always

$Cost(h\theta(x), y) = -ylog(h\theta(x)) - (1-y)log(1-h\theta(x))$
将代价函数优化为1行
即： $j(\theta) = \frac{1}{m}Cost(h\theta(x^{(i)}), y^{(x)}) = -\frac{1}{m}[\sum\limits_{i=1}^{m}y^{(i)}log(h\theta(x^{(i)})) + (1-y^{(i)})log(1-h\theta(x^{(i)}))$

问题:如何不断的拟合 $\theta$ 期望为 $\min J(\theta)$ 最小化代价函数 — 使得拟合模型

易于分类
目标对新的输入变量x输出正确的预测
下一步目标如何最大限度最小化代价函数 — 向量化实现
这里写图片描述

下一步目标如何最大限度最小化代价函数 — 向量化实现
采用梯度下降法
$j(\theta)= -\frac{1}{m}[\sum\limits_{i=1}^{m}y^{(i)}log(h\theta(x^{(i)})) + (1-y^{(i)})log(1-h\theta(x^{(i)}))$
want $\min J(\theta)$ :
$repeat{ \theta_j := \theta_j - \alpha \sum\limits_{i=1}^{n} (h\theta(x^{(i)}) - y^{(i)})x^{(i)} }$

问题: 线性回归和逻辑回归是一个梯度下降算法么
    完全不是 两者的假设函数不同
问题: 如何监测梯度下降 确保它收敛
    带入了代价函数 偏导数 实质上 会想最优或者局部最优点梯度下降


    小结: 假设函数 sigmoid
        代价函数 化简 -- 非凸性函数转化为凸性函数
        梯度下降法

高级优化算法 optimization algorithm

$cost function J(\theta)$ 代价函数
$want \min J(\theta)$ 目标最小化代价函数
给定 $\theta$ 用计算机实现计算
— $\theta$ 代价函数
—$代价函数的偏导数确保收敛性—计算代价函数及代价函数的收敛性

梯度下降法
$repeat{ \theta_j = \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta) }$
$\frac{\partial}{\partial \theta_j} J(\theta) = \sum\limits_{i=1}^{m}(h\theta(x^{(i)}) - y^{(i)})x_j^{(i)}$
除了梯度下降法还有
共轭梯度法 conjugate gradient
变尺度法 BFGS
限制尺度法 L-BFGS

    这些算法都是对代价函数的不同优化
    优点: 不需要手动计算学习速率
            收敛速度快于梯度下降法
    缺点:
            过于复杂

obtave 如何使用梯度下降法计算
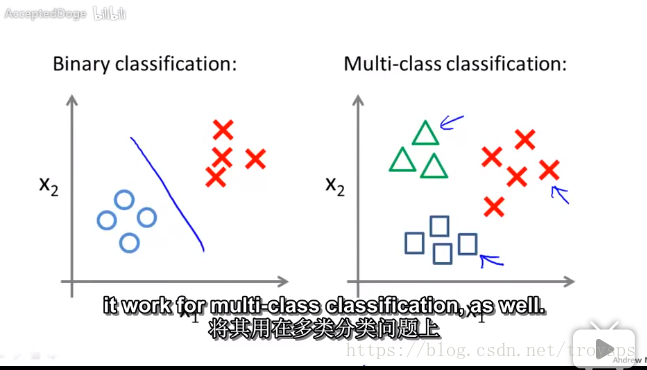
这里写图片描述

多分类问题

本质上来说 求得是 $\max p(y=i|x_i, \theta) i=1,2,3....$
概率最大化问题

这里写图片描述
参考文献
斯坦福机器学习课程吴恩达

logistics regression原理与线性回归