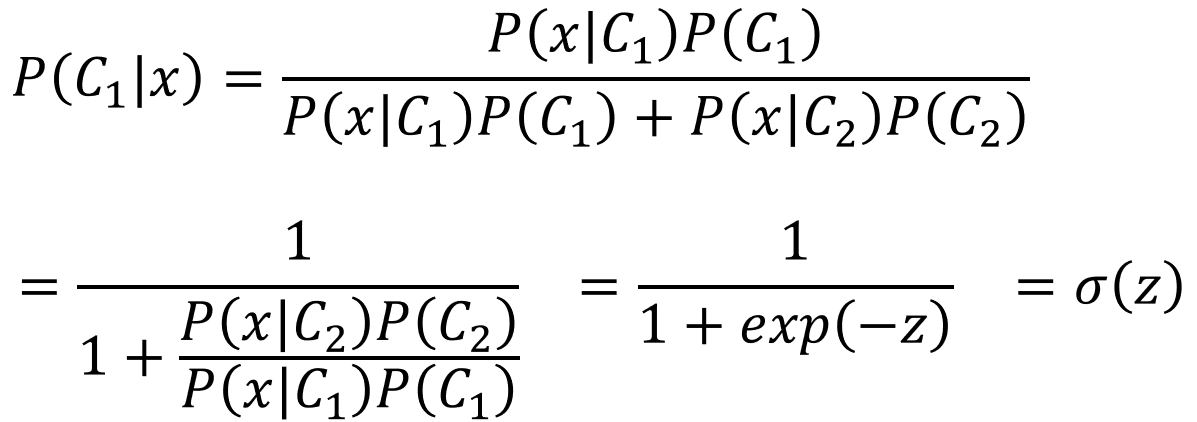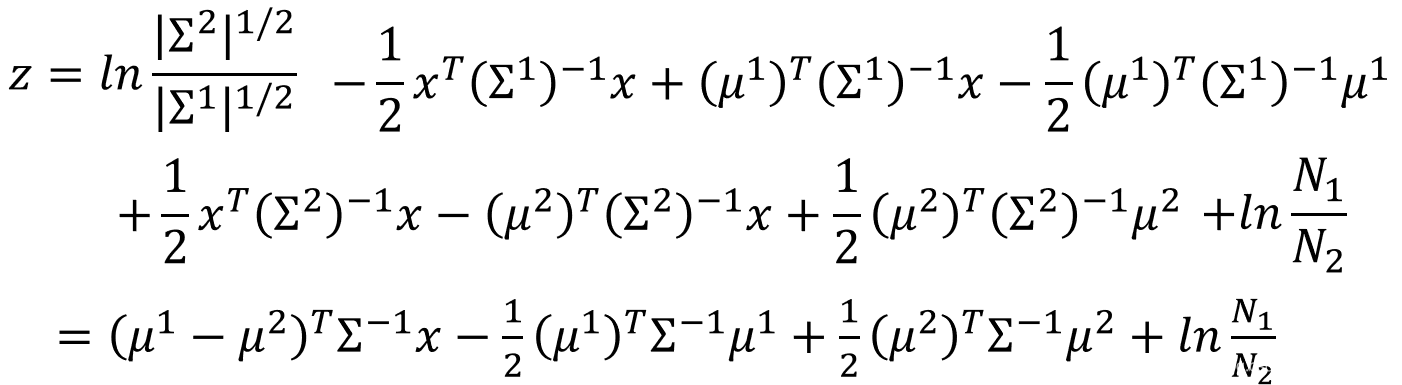[Machine Learning] 逻辑回归（Logistics Regression）

引言

Logistics回归，虽然这个算法从名字上来看是回归算法，但实际上是一个分类算法。

Logistics回归是在线性回归的基础上，使用sigmoid函数，将线性模型 $\omega x+b$ 的结果压缩到 $[0,1]$ 之间，使其有概率意义。

Logistics回归本质仍然是一个线性模型，虽然在线性模型 $\omega x+b$ 的基础上加入sigmoid函数后使其非线性化，但是这个非线性化的作用只是为了分类（Classification），并非为了将样本数据进行特征变换（Feature Transformation），因此，Logistics只能解决线性可分的问题。

Logistics回归属于概率性判别式模型，即：

Logistics回归模型是具有概率意义的
Logistics回归并没有对数据的分布进行建模，也就是说，Logistics Regression并不知道数据的具体分布，而是直接将判别函数，或者说是分类超平面求解了出来。（具体可参考《[Machine Learning] 生成模型 & 判别模型（Generative & Discriminative Model）》一文）

思维引导

以下内容涉及贝叶斯公式、后验概率等内容，想具体了解可参考《[Machine Learning] 贝叶斯公式 & 全概率公式（Bayes Rule & Total Probability Theorem）》一文

一般来说，分类算法都是求解 $p(C_k|x)$ ，即对于一个新的样本，计算其条件概率 $p(C_k|x)$ 。这个可以看作是一个后验概率，其计算可以基于贝叶斯公式得到：

$p(C_k|x) = \frac{p(x|C_k)p(C_k)}{\sum_{k=1}^Kp(x|C_k)p(C_k)}$

其中 $p(x|C_k)$ 是类条件概率密度， $p(C_k)$ 是类的先验概率。使用这种方法的模型，称为是生成模型，即： $p(C_k|x)$ 是由 $p(x|C_k)$ 和 $p(C_k)$ 生成的。

尝试生成模型做分类

如果有n个特征数为m的样本数据（已分为两类），即：

$((X^1,y^1),(X^2,y^2),...,(X^n,y^n))$

其中 $X^i = (x^i_1,x^i_2,...,x^i_m)(i = 1,2,...,n)$ ， $y^i\in \{0,1\}$

现在出现了一个新的样本 $X$ ，让你判断这个 $X$ 属于哪一类？（0还是1）

如果我们用生成模型的话，假设CLass 1代表1类，Class 2代表0类，由贝叶斯公式：

$p(C_1|x) = \frac{p(x|C_1)p(C_1)}{p(x|C_1)p(C_1)+p(x|C_2)p(C_2)}$

其实这个上面的这个式子，我们可以试着推导一下，即:

其中， $z =ln \frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)}$ ，突然发现，我们一不小心推导出了一个sigmoid函数，但是我们先不管，我们继续用生成模型。

那么现在我们只要确定了 $z$ 中的 $P(x|C_1)、P(x|C_2)、P(C_1)、P(C_2)$ ，我们就可以确定后验概率 $p(C_1|x)$ 。

假设Class 1的数量为 $N_1$ ，Class_2的数量为 $N_2$ 。

确定 $P(C_1)$

$P(C_1) = \frac{N_1}{N_1+N_2}$
确定 $P(C_2)$

$P(C_2) = \frac{N_2}{N_1+N_2}$
确定 $P(x|C_1)、P(x|C_2)$

由于已知样本数量有限，所以我们无法通过已知样本数据确定样本的分布情况，那我们应该怎么做呢？（可参考《[Machine Learning] 极大似然估计（Maximum Likelihood Estimate）》）

我们假设样本满足高斯分布（只是举个例子，只要满足指数族分布即可），即：

提示： $\mu,\Sigma$ 是参数，可用极大似然估计做参数估计得出！
确定 $z$

--------------------------------Warning Of Math--------------------------------

综上，我们可以推导：

其中，又有：

--------------------------------End Of Warning--------------------------------

因此，最终有：

这里会发现，这个式子很复杂很复杂，我们可以做这样的假设： $\Sigma_1 = \Sigma_2 = \Sigma$ ，即两个高斯分布共享相同的协方差矩阵（Covariance Matrix），这样做的理由是：
- 协方差矩阵的大小与特征数m有关，即如果特征数为2，则协方差矩阵大小为 $2\times2$ ，如果特征数为100，则协方差矩阵大小为 $100\times100$ ，因此，协方差矩阵的大小与特征数的平方成正比。
- 协方差矩阵是Model要学习的参数，但是协方差矩阵的大小与特征数的平方成正比，如果特征数很大，那么要学习的参数就很多，在《[Machine Learning] 欠拟合 & 过拟合（Underfitting & Overfitting）》一文中提到过，参数过多，可能会导致过拟合现象，从而使得测试集数据效果大打折扣。
因此，共享相同的协方差矩阵可以减少参数，有效减少过拟合产生的影响。

现在，我们化简 $z$ 后发现：

如果我们令：
$\omega^T = (\mu^1-\mu^2)^T\Sigma^{-1}$

$b = -\frac{1}{2}(\mu^1)^T\Sigma^{-1}\mu^1 + \frac{1}{2}(\mu^2)^T\Sigma^{-1}\mu^2 + ln\frac{N_1}{N_2}$

最终，我们可以得到一个式子（其实不共享协方差矩阵也可以得到这个结果，只是为了提供一种降低过拟合现象影响的思路）：

$P(C_1|x) = \sigma(\omega\cdot x+b)$

等等！那我们可不可以直接通过学习 $\omega(Size:1\times m)$ 和 $b(Size:1\times m)$ 来确定 $P(C_1|x)$ 呢？这样子就不用大费周章的使用生成模型去学习估计参数 $\mu_1(Size:1\times m),\mu_2(Size:1\times m),\Sigma(Size:m\times m)$ （况且参数这么大，还有可能过拟合）。

答案是可以的！这样子直接确定 $P(C_1|x)$ 的模型叫做判别模型。同时，上式的模型也就是我们今天要说的模型：Logistics回归模型。

Logistics回归的优点

直接对分类的概率建模，无需实现假设数据分布（比如刚才的生成模型中我们假设了高斯分布），从而避免了假设分布不准确带来的问题；
不仅可预测出类别，还能得到该预测的概率，这对一些利用概率辅助决策的任务很有用；
$z$ 函数（也叫对数几率函数）是任意阶可导的凸函数，有许多数值优化算法都可以求出最优解。

Logistics Regression

Step1：Function Set

由上图，所以Logistics回归的Model为：

$P_{\omega,b}(C_1|x) = f_{\omega,b}(x) = \sigma(z)$

$z = \omega x+b = \sum_i\omega_i x_i +b$

$\sigma(z) = \frac{1}{1+\exp(-z)}$

Step2：Goodness of a function

逻辑回归模型的数学形式确定后，剩下就是如何去求解模型中的参数。在统计学中，常常使用极大似然估计法来求解，即找到一组参数 $\omega^*,b^*$ ，使得在这组参数下，我们的数据的似然度（概率）最大。

使得似然函数：

$L(\omega,b) = f_{\omega,b}(x^1)f_{\omega,b}(x^2)(1-f_{\omega,b}(x^3))…f_{\omega,b}(x^N)$

有：

$\omega^*,b^* = arg\max_{\omega,b}$

为了更方便求解，我们对等式两边同取对数，写成对数似然函数：

$-lnL(\omega,b) = -[lnf_{\omega,b}(x^1) + lnf_{\omega,b}(x^2) + ln(1-f_{\omega,b}(x^3)) + … + lnf_{\omega,b}(x^N)]$

有：

$\omega^*,b^* = arg\max_{\omega,b}L(\omega,b) = arg\min_{\omega,b}-lnL(\omega,b)$

现在做出如下假设：

其中， $\hat{y}^i$ 表示实际值。

则有：

$\ \ \ \ \ -lnL(\omega,b) = -[lnf_{\omega,b}(x^1) + lnf_{\omega,b}(x^2) + ln(1-f_{\omega,b}(x^3)) + … + lnf_{\omega,b}(x^N)]$

$= \sum_n-[\hat{y}^nlnf_{\omega,b}(x^n) + (1-\hat{y}^n )ln(1-f_{\omega,b}(x^n))]$

上式即为交叉熵损失函数（CrossEntropy Loss），为什么不用Square Loss呢？具体可参考《[Machine Learning] 交叉熵损失函数 v.s. 平方损失函数（CrossEntropy Loss v.s. Square Loss）》一文。

Step3：Find the best Function

$\frac{\partial(-lnL(\omega,b))}{\partial{\omega_i}} = \sum_n-[\hat{y}^n\frac{\partial lnf_{\omega,b}(x^n)}{\partial{\omega_i}} + (1-\hat{y}^n )\frac{\partial{ln(1-f_{\omega,b}(x^n))}}{\partial{\omega_i}}]$

其中：

$\frac{\partial lnf_{\omega,b}(x^n)}{\partial{\omega_i}} = \frac{\partial lnf_{\omega,b}(x^n)}{\partial z}\frac{\partial z}{\partial{\omega_i}}= \frac{\partial ln\sigma(z)}{\partial z}\frac{\partial (\sum_i\omega_i x_i^n +b)}{\partial{\omega_i}}$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \frac{1}{\sigma(z)}\frac{\partial \sigma(z)}{\partial z}x_i^n = (1-\sigma(z))x_i^n = (1-f_{\omega,b}(x^n))x_i^n$

$\frac{\partial ln(1-f_{\omega,b}(x^n))}{\partial{\omega_i}} = \frac{\partial ln(1-f_{\omega,b}(x^n))}{\partial z}\frac{\partial z}{\partial{\omega_i}}= \frac{\partial ln(1-\sigma(z))}{\partial z}\frac{\partial (\sum_i\omega_i x_i^n +b)}{\partial{\omega_i}}$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =- \frac{1}{1-\sigma(z)}\frac{\partial \sigma(z)}{\partial z}x_i^n = -\sigma(z) x_i^n = -f_{\omega,b}(x^n)x_i^n$

则：

$\ \ \ \ \ \ \ \ \frac{\partial(-lnL(\omega,b))}{\partial{\omega_i}} = \sum_n-[\hat{y}^n\frac{\partial lnf_{\omega,b}(x^n)}{\partial{\omega_i}} + (1-\hat{y}^n )\frac{\partial{ln(1-f_{\omega,b}(x^n))}}{\partial{\omega_i}}]$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \sum_n-[\hat{y}^n(1-f_{\omega,b}(x^n))x_i^n + (1-\hat{y}^n )(-f_{\omega,b}(x^n)x_i^n)$

$= \sum_n-(\hat{y}^n-f_{\omega,b}(x^n))x_i^n$

因此， $\omega_i$ 的更新公式为：

$\omega_i \leftarrow \omega_i-\eta \sum_n-(\hat{y}^n-f_{\omega,b}(x^n))x_i^n$

Logistics Regression v.s. Linear Regression

对比逻辑回归和线性回归，可以发现他们的参数更新公式是一致的！

但是逻辑回归是用于处理分类问题，线性回归是用来处理回归问题！

Oh_MyBug

发布了36 篇原创文章 · 获赞 3 · 访问量 6230

私信关注