人工智能10大算法-逻辑回归(logistics regression)

逻辑回归是一个二分类问题

二分类问题

二分类问题是指预测的y值只有2个取值(0或1),二分类问题可以扩展到多分类问题.例如:我们要做一个垃圾邮件过滤系统, $x^i$是邮件的特征,预测的y值就是邮件的类别,是垃圾邮件还是正常邮件.对于类别我们通常称为正类(positive class)和负类(negative class),垃圾邮件的例子中,正类就是正常邮件,负类就是垃圾邮件

逻辑回归

Logistic函数

如果我们忽略二分类问题中y的取值是一个离散的取值(0或1),我们继续使用线性回归来预测y的取值.这样会导致y的取值并不为0或1.逻辑回归使用一个函数来归一化y值,使y的取值在(0,1)之间,这个函数称为Logistic函数(Logistic function),也称为Sigmoid函数,公式如下
g(z) = $\frac{1}{1 + ^{e^{-z}}}$
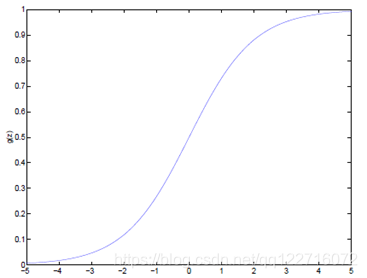
Logistic函数当z趋近于无穷大时,g(z)趋近于1;当z趋近于无穷小时,g(z)趋近于0
Logistic函数图如下:

Logistic函数求导时有一个特征
$g^/$(z) = $\frac{d}{dz}$ $\frac{1}{1+e^{-z}}$
= $\frac{1}{(1+e^{-z})^2}$( $e^{-z}$)
= $\frac{1}{1+e^{-z}}$(1- $\frac{1}{(1+e^{-z})}$)
=g(z)*(1-g(z))

逻辑回归表达式

逻辑回归本质上是线性回归,只是在特征到结果的映射中加入了一层函数映射,即先把特征线性求和,然后使用函数g(z)将最为假设函数来预测.g(z)可以将连续值映射到0和1之间.线性回归模型的表达式代入g(z),就得到逻辑回归的表达式:
$h_\theta(x) = g(\theta^Tx) = \frac{1}{1 + e^{-\theta}}$
这里为什么用 $h_\theta(x)$:hyperthesis:假设
令 $x_0 = 1$，
$\theta^Tx = \theta_0 + \sum_{j=0}^{n}\theta_jx_j$

逻辑回归的软分类

现在我们将y的取值 $h_\theta(x)$通过Logistic函数归一化到(0,1)间,y的取值特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
$P(y=1|x;\theta) = h_\theta(x)$
$P(y=0|x;\theta) = 1-h_\theta(x)$
对上面的表达式合并:
$P(y|x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y}$
解释:当y=0时, $P(y|x;\theta)=1-h_\theta(x)$.当y=1时, $P(y|x;\theta)=h_\theta(x)$

梯度上升

得到逻辑回归的表达式,下一步和线性回归类似.构建似然函数,然后最大似然估计,最终推导出 $\theta$的迭代更新表达式,这个请参考文章《线性回归、梯度下降》,只不过这里用的不是梯度下降,而是梯度上升,因为这里是最大化似然函数不是最小化似然函数.
似然函数表达式:
$L(_\theta)=p(\vec{y}|X;\theta)$
= $\prod_{i=1}^{m}p(y^{(i)}|x^{i};\theta)$
= $\prod_{i=1}^{m}(h_\theta(x^{i}))^{y^{(i)}}(1-h_\theta(x^{i}))^{1-y^{i}}$
对似然函数取 $\log$:即逻辑回归的损失函数
$\Psi(\theta)=\log{L(\theta)}$
= $\sum_{i=1}^{m}y^{(i)}\log{h(x^{(i)})+(1-y^{(i)})\log{(1-h(x^{(i)})}})$
转换后的似然函数对 $\theta$求偏导,
$\frac{\alpha}{\alpha\theta_j}\Psi(\theta)$
= $(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(\theta^Tx)})\frac{\alpha}{\alpha\theta_j}g(\theta^Tx)$
= $(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(\theta^Tx)})g(\theta^Tx)(1-g(\theta^Tx)\frac{\alpha}{\alpha\theta_j})\theta^Tx$
= $(y(1-g(\theta^Tx))-(1-y)g(\theta^Tx))x_j$
= $(y-h_\theta(x))x_j$
这个求导过程第一步是对 $\theta$偏导的转化,一句偏导公式: $y=\ln{x}$; $y^/=\frac{1}{x}$

• 第二步是根据个g(z)求导的特性: $g^/(z)=g(z)(1-g(z))$
• 第三步就是普通的变换
  这样我们就得到了梯度上升每次迭代的更新时间,那么 $\theta$的迭代表达式为:
  $\theta_j:=\theta_j+\alpha(y{(i)}-h_\theta(x^{(i)}))x_j^{(i)}$
  这个表达式域LMS算法的表达式相比,看上去完全相同,但是梯度上升与LMS是两个不同的算法,因为 $h_\theta(x^i)$表示的是关于 $\theta^Tx$的一个非线性函数.两个不同的算法,同一个表达式表达,这并不仅仅是巧合,两者存在深层次的联系.这个问题,我们将在广义线性模型GLM中解答