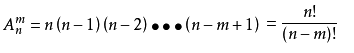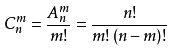可汗学院统计学17-24课笔记

[第17课] 随机变量介绍

离散随机变量（discrete random variable）
在一定区间内变量取值为有限个，如抛硬币，掷骰子

连续随机变量（continuous random variable）
在一定区间内变量取值为无限个，如明天下雨的概率，在(0,1)之间

random.randint()与np.random.randint()的区别
random.randint()方法里面的取值区间是前闭后闭区间，而np.random.randint()方法的取值区间是前闭后开区间

import random

# 离散随机变量（discrete random variable）
# 如：抛硬币
x = random.randint(0, 1)
print(x)

# 掷骰子
x = random.randint(1, 6)
print(x)


# 连续随机变量（continuous random variable）
x = random.random()
print(x)

1
6
0.7703803681713864

[第18课] 随机变量介绍

摘自《统计学18：随机变量介绍》,略有修改

概率密度函数

• 随机变量所有值发生概率和等于1
• 概率密度函数是对连续随机变量而言的．

比如说明天下雨的概率是0.8，那么不下雨的概率是0.2；

观察密度函数的图，面积才是表示密度函数的概率值．而不是x对应y坐标．

假设曲线为f(x)，概率是面积，也就是对函数f(x)的积分：

$P(0.1<X<0.2)=\int_{0.1}^{0.2}f(x)d(x)$

其中 $\int_{-\infty }^{+\infty }{f(x)d(x)}=1$

离散的随机变量概率

区别于连续随机变量，离散变量的概率是可以枚举出来的，如掷骰子，有六个离散变量，每个离散变量的概率都是 $1\over6$

[第19课] 二项分布1

摘自《统计学19：二项分布1》,略有修改

看一下掷硬币的问题
掷一次硬币正面或者反面发生的概率都是 $\frac{1}{2}$

掷五次硬币或者一次掷五个硬币（每个硬币正反独立的，每次硬币独立的，怎么操作都一样．），记出现正面的数量为 $X$.

$P(X=0)$（出现正面为0次的概率，也就是五次全为反面）？

全为反面只有一种情况，就是第一次投掷为反，第二次为反．．．

$P(X=0)=\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{1}{32}$

$P(X=1)$（出现正面为1次的概率）？

正面为1次有5种情况，就是第一次投掷为正，其他全为反；第二次为正，其他全为反．．．
每中情况都是 $\frac{1}{32}$（出现正面的次数和非正面的次数都是 $\frac{1}{2}$）

$P(X=1)=5 \times \frac{1}{32} = \frac{5}{32}$
$P(X=2)$（出现正面为2次的概率）？

还要枚举吗？好像有点累
分析一下：

• 先确定一个正面发生的位置，它有5种（第一次投掷为正，第二次为正．．．），再确定第二个正面发生的位置，第一个记录已经占走了一个位置，还有四个位置选一个为正，有4种．　 $5 \times 4$
• 刚刚我们先确定了，再确定，多做了排序，也就是同样第二次和第三次为正，但是我们却在刚刚把它记为了两种情况（先找到2位再发现3，和先找到3再发现2）我们要排除我们不必要的排序．　 $\frac{5 \times 4}{2}$
• 每中情况都是 $\frac{1}{32}$

$P(X=2)=\frac{5 \times 4}{2} \times \frac{1}{32} = \frac{5}{16}$
$P(X=3)$？

• 确定第一个（5个位置选1个），第二个（4个位置选1个），第三个（3个位置选1个） $5 \times 4 \times 3$
• 排除不必要的排序（3个的排序为 $3 \times 2$）．　 $\frac{5 \times 4 \times 3}{3 \times 2}$
• 每中情况都是 $\frac{1}{32}$

$P(X=3)=\frac{5 \times 4 \times 3}{3 \times 2} \times \frac{1}{32} = \frac{5}{16}$
$P(X=4)$？

• $A_5^4 = 5 \times 4 \times 3 \times 2$
• $\frac{A_5^4}{A_4^4} = \frac{5 \times 4 \times 3 \times 2}{4 \times 3 \times 2}$
• $\frac{1}{32}$

$P(X=4)=\frac{5 \times 4 \times 3 \times 2}{4 \times 3 \times 2} \times \frac{1}{32} = \frac{5}{32}$
$P(X=5)$？
$P(X=5)=C_5^5 \times \frac{1}{32} = \frac{1}{32}$

也可以把5次为正理解为0次为反，正反概率相等，那么 $P(X=5)＝P(X=0)$

二项分布就是重复n次独立的伯努利试验.
伯努利实验:在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变

[第20课] 二项分布2

摘自《统计学20：二项分布2》,略有修改

随机变量是一种映射关系．还是以上一节投掷硬币情况为例

$X= \begin{cases} 0 & \text{全为反面}\\ 1 & \text{有$1$次为正面}\\ 2 & \text{有$2$次为正面}\\ 3 & \text{有$3$次为正面}\\ 4 & \text{有$4$次为正面}\\ 5 & \text{全为正面}\\ \end{cases}$

把上概率整理如下图表：

如果投掷的次数非常的多，把它们的概率值用曲线描出来，就是一根钟形曲线．在离散中是二项分布，在连续中它是正态分布．

二项分布是可以被总结出公式的．

还记得上一节我在最后的 $P(X=5)$求解时，把系数（后面是每次独立发生的概率值）写了 $C_5^5$吗？

$C_n^m$表示从 $n$个元素中挑选出 $m$个元素（无序）的可能．（也可以理解为从 $n$次实验中发生 $m$次同事件的可能）

二项式系数公式

$(_m^n)=C_n^m = \frac{n!}{m!(n-m)!}$

也可以继续上一节那个分析， $\frac{A_n^m}{A_m^m}$记为 $C_n^m$

其中：

有了二项式系数其实就是从 $n$次实验中发生 $m$次同事件的可能种类数，然后它乘一每次事件的概率就是我们求的 $P(X=m)$．

那么二项式分布 $X～B(n,p)$的公式就来了：

$P(k,n,p) = P(X=k) = C_n^kp^k(1-P)^{n-k}$

[第21课] 二项分布3

摘自《统计学21：二项分布3》,略有修改

来看上一节留下的公式
$P(X=k) = C_n^kp^k(1-p)^{n-k}$

你可能已经明白了二项系数 $C_n^k$什么意思，这里说一下为什么是概率是 $p^k(1-p)^{n-k}$．
可能硬币事件的两种结果让我记住了 $\frac{1}{2}$,那是一个比较特殊的情况．如果把事件转换为掷筛子呢？它就不再是 $\frac{1}{2}$, $\frac{1}{2}$．

如果问题转换为掷筛子，点数为1或者2则甲胜出，点数为3或者4则乙胜出，点数为5或者6则丙胜出，现在寻找在n次实验中，甲胜出X次的概率？

只关心甲的概率，只需知道是甲赢了，还是输了，并不关心乙或者丙赢了他．现在就是二项分布了，甲赢（点数为1或2），甲不赢（点数不为1或2，即为3，4，5，6）．则事件发生的概率分别为甲赢 $\frac{1}{3}$，甲不赢 $\frac{2}{3}$．
注意二项分布的特点，每次投掷都是独立的，不受之前实验的影响，每次结果都是甲赢 $\frac{1}{3}$，甲不赢 $\frac{2}{3}$．

那么求 $P(X=0)$,假设投掷了8次：

• 通过上一节我们知道系数 $C_8^0$
• 甲赢的次数为0，那么这种可能就是全输的概率，就是每次概率是 $\frac{2}{3}$，则 $P(X=0)=C_8^0 \times (\frac{2}{3})^8$

$P(X=1)$：

• 系数 $C_8^1$
• 甲赢的次数为1，那么这种可能就是1次为胜，7次为输的概率.即8次事件中，发生了1次概率是 $\frac{1}{3}$事件和 $(8-1)$次概率为 $\frac{2}{3}$事件，则 $P(X=1)=C_8^1 \times (\frac{1}{3})^{1} \times (\frac{2}{3})^{8-1}$

$P(X=2)$：

• 系数 $C_8^2$
• 发生了2次概率是 $\frac{1}{3}$事件和 $(8-2)$次概率为 $1-\frac{1}{3}$事件（两种结果，总的概率为1），则 $P(X=2)=C_8^2 \times (\frac{1}{3})^{2} \times (1-\frac{1}{3})^{8-2}$

沿着这个方法走下去，就会发现如何去利用公式了．

[第22课] 二项分布4

这一节是介绍用Excel绘制二项分布，详情请看《统计学22：二项分布4》

[第23课] 期望值E(X)

摘自《统计学23：期望值E(X)》，略有修改

给出一个总体，一组数： 3, 3, 3, 4, 5

它的平均数是：　 $\frac{3+3+3+4+5}{5}=\frac{18}{5}=3.6$

我们可以换一种方式来看，里面有3个3，1个4，1个5： $\frac{3(3)+1(4)+1(5)}{5}=\frac{3}{5}×3+\frac{1}{5}×4+\frac{1}{5}×5 = 60$

频率

观察这个式子，60%×3+20%×4+20%×5，这里没有表示每个数字出现的次数，只是它出现的频率：

3的频率是60%,4的频率是20%,5的频率是20%.计算是1.8+0.8+1＝3.6

知道3，4，5每个数字相对的频率，也就是占总体额百分比，就可以计算除均值．

[第24课] 二项分布的期望值

摘自《统计学24：二项分布的期望值》，略有修改
假设随机变量X表示n次实验的次数，其中每次成功的概率是p.

$E(X) = np$

在二项分布中，期望值可以看成是最可能得到的那个结果．

假设投篮的命中概率为40％，投10次．
那么 $E(X) = np = 10 \times 40\% =4$

可以理解为命中概率为40％，那么投10次，可能4次命中．

回顾二项式概率的公式：

$P(X=k) = C_n^kp^k(1-p)^{n-k}$

期望值公式：

$\begin{aligned} E(X) &= \sum_{k=0}^nkP(X=k) \\ &=\sum_{k=0}^nC_n^kkp^k(1-p)^{n-k}\\ &=0C_n^0p^0(1-p)^{n-0}+1C_n^1p^1(1-p)^{n-1}+…+nC_n^np^n(1-p)^{n-n}\\ &=1C_n^1p^1(1-p)^{n-1}+…+nC_n^np^n(1-p)^{n-n} \\ &=\sum _{k=1}^nC_n^kp^k(1-p)^{n-k}\\ \end{aligned}$

代入二项式系数：

$C_n^k=\frac{n!}{k!(n-k)!}$

得到：

$\begin{aligned} E(X) &=\sum _{k=1}^n \frac{n!}{k!(n-k)!} k p^k(1-p)^{n-k}\\ &=\sum _{k=1}^n \frac{n!}{k(k-1)!(n-k)!} k p^k(1-p)^{n-k}\\ &=\sum _{k=1}^n \frac{n!}{(k-1)!(n-k)!} p^k(1-p)^{n-k}\\ &=\sum _{k=1}^n \frac{n(n-1)!}{(k-1)!(n-k)!} pp^{k-1}(1-p)^{n-k}\\ &=np\sum _{k=1}^n \frac{(n-1)!}{(k-1)!(n-k)!} p^{k-1}(1-p)^{n-k} \end{aligned}$

令 $a=k-1,b=n-1$，则 $n-k=b-a$，得到：

$\begin{aligned} E(X) &=np\sum _{a=0}^b \frac{(b)!}{a!(b-a)!} p^{a}(1-p)^{b-a}\\ &=np\sum_{a=0}^b C_b^a p^{a}(1-p)^{b-a}\\ &= np \end{aligned}$

$\sum\limits_{a=0}^b C_b^a p^{a}(1-p)^{b-a}$表示一个二项分布的概率和，和应该为1

主要参考资料：

视频：《可汗学院统计学》
文章：csdn shangboerds 学习笔记
Jent’s Blog 学习笔记（后来发现的，写得很好，推荐）