写在前面的话:
《统计学完全教程》囊括了统计学的全部知识,共22章,由美国著名的学者沃塞曼所著。在nlp领域里统计学占据主导地位,没有了统计学,深度学习将无法构建损失函数,无法实现图模型的推理。推理算法主要依靠统计学,包括以拉普拉斯矩阵为基础的无向图卷积算子,上个世纪的PageRank算法,随机游走模型……当今的AI主要以从海量数据中寻找规律的方式来实现弱人工智能,包括特征的抽取(比如图卷积算子,谱卷积算子)和统计概率推理两大形式。最终联结主义还是要统一于统计学的范畴,没有了统计学,当今的AI什么都不是。今年nlp领域里进展最大的就是谷歌大脑和DeepMind的GN block了,把神经网络和图模型统一起来,也可以理解为推理领域的一个大进展,统一了之前的研究,包括以色列特拉维夫大学和哈弗大学之前发布的一篇关于有向图模型推理的谱卷积算子的论文。在15年的时候,把CRF神经网络化是这个领域的一个尝试,已经获得了成功。接下来的推理研究,除了尝试以上融合联结主义和结构方法的思路外,更应该关注规则和专家系统。推理是离不开基的,规则总是有限的,但是人类认识的事物总是无限的。比如总结哺乳动物区别于其他动物的特征时,在观察了不同种类的大量的哺乳动物与其他动物的行为后,会发现他们既有共性,又有差异。我们重点关注的是差异化:胎生和哺乳。其他的重叠特征忽略!那么运用统计学进行推理主要就是从这些数据中总结出事物最根本的独特的特征,以实现推理。这种思路,可以摆脱在训练过程中高度依赖海量数据的笨重式的方法(比如当今的深度学习)。当然,人工要想实现更加智能化,必须组织行业内专家去发现规则,然后抽象化(规则早已经存在,人类要做的是去发现它,至于规则是不是上帝制定的,只有牛顿和爱因斯坦思考过,哈哈)。物理学,神经生物学都可以看作是规则,数学更是。顺着这个思路,我们发现当今的AI研究领域和项目里面,只有知识图谱最符合这个需求,其他的都是浮云。大力推进知识图谱和深化知识图谱是下一代AI必须做的事情,比如研发具有CVT(虚拟节点)的图谱,增加知识的时空表示,引入因果关系推理,而不只是仅限于RDF的三元组形式。可以说知识图谱将大有作为,研究知识图谱和本体论的门槛将远高于深度学习。按照深度学习的思路,Ai必然会走入死胡同,是没有大的进展的。
在研究和学习AI的过程中,开头是很难占到一定高度去研究的,基本上先是拓展广度,然后才会有深度。而且经历了前期的走弯路,摸索,思考后,后期会进行整合,整合之后才算真正入门了。入门就意味着有了自己确定的研究课题,有着持久的研究兴趣,很明显从学位上看,只有到了博士才可以达到这个要求。这就是国内的研究生需要考博的原因,研究生对研究并不太感兴趣,说明国内的研究生入学考试和教学存在大问题。前期需要大量阅读文献,包括谷歌大脑,DeepMind等的论文,从这些文献中吸收思想和观点比学习知识本身更重要。而并不是找来一大堆论文从中找套路,为了发论文而发论文。这样的研究掉书袋和沽名钓誉的成分高一些。目前国内部分的深度学习研究,给人一种找套路的感觉,至于是不是只有研究者自己知道。个人认为发出一篇研究下一代AI的高水平论文很不容易。知识永远是有限的(就像规则一样),然而这些知识的组合却是无限的,规则创造了新的东西。比如当今的统计学派和联结主义学派之争,很显然联结主义学派并没有统计学派卡看透事物的本质,只是很初级的一种AI。唯一的出路就是两者结合,同时需要大量的规则。
同样是研究过去,如果有着明确的目标,换一种角度站在更高的视野重新研究,会对未来产生深远影响。但如果是为了学习知识和做工程,也无可厚非,只不过会很被动。什么是创新?比如我发现了原来的早已经存在的两个算法之间新的关联,这个新的联系就是创新。没有对过去的思考和总结,就不会产生创新,当然更需要跳出过去的框框。那么当前的深度学习的研究,对nlp来说,意义并不是很大,重点应该关注统计学派和知识图谱。这两者更能揭示事物的本质。比如有向动态图模型HMM是非常好的推理算法,不仅限于nlp领域。
本篇笔记是统计学中的第一部分:随机变量。
1.随机变量的含义


2.CDF和PDF




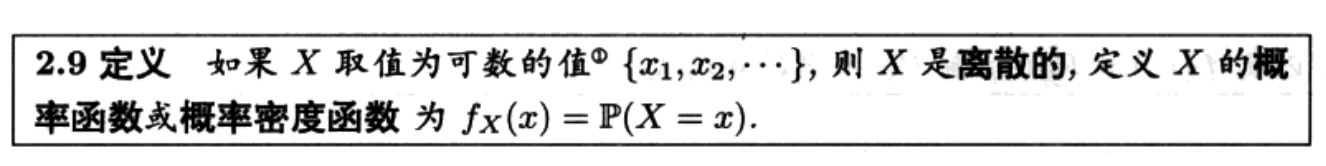
如果变量是离散的,概率测度p(x)和概率密度相等,如果是连续的,概率测度是概率密度的积分。
概率测度,累积分布函数和概率密度函数的关系:


概率密度函数:

学过定积分和微分的都知道,CDF是PDF的原函数,概率密度反映了概率分布情况,密度大的区域说明此区域概率质量比较大,还可以反映出概率分布的均匀情况。从CDF来看,阶梯递增函数两个区间的差比如F(b)-F(a)正好反映了此区间的概率分布情况,它是概率密度函数的积分。


一些重要的离散随机变量

这里重点介绍伯努利分布和二项式分布

重要的连续随机变量:高斯分布
正态分布与中心极限定理有关联。在最一般的形式中,在某些条件下(包括有限方差),它指出独立于独立分布的随机变量观测样本的平均值在分布上收敛到正态,当观测数量足够大时,它们就变成正态分布。比如最小二乘法适应于正态分布。
正态分布有时被非正式地称为钟形曲线。但是具备钟形曲线的不都是正态分布,比如如下本人手绘的图:

在局部attention的过程中,运用了钟形曲线,距离中心点越远的点影响力也就是权值越小,但它不是高斯分布。
高斯分布的概率密度为:
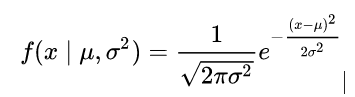
标准高斯分布,也就是均值为零,标准差为1:
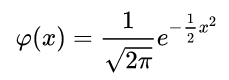
如果一个随机变量遵循高斯分布,我们通常记为:
![]()
高斯分布的一些性质:
①正态分布是椭圆分布的一个子类。正态分布关于其平均值是对称的,在整个实线上是非零的。因此,它可能不适合于固有为正的或者强烈倾斜的变量,例如一个人的体重或者股票的价格。这些变量可以通过其他分布更好地描述,例如对数正态分布或帕累托分布。也就是说我们关注的是重尾分布的这些数据,高斯分布是不适合的。
②当值x与平均值相差超过几个标准偏差时,正态分布的值实际上为零(例如,三个标准偏差的分布覆盖了总分布的绝大部分,剩下0.27%几乎可以忽略了)。
③高斯分布属于稳定分布族,不管其均值或方差是否是有限的,它都是独立同分布分布。除了作为极限情况的高斯分布外,所有的稳定分布都具有重尾和无穷方差。它是少数几个稳定且具有可解析表达的概率密度函数的分布之一,其他的是Cauchy分布和Lévy分布。

关于高斯分布的傅立叶变换和矩母函数后面的博客论述。
除此之外高斯分布具有以下最基础的性质:


二元分布和独立分布:

![]()




