[统计学笔记] 统计学计算题选讲（精华）

统计学计算题选讲

第 1 题

某班级学生物理课程考试成绩分别为:

68 89 88 84 86 87 75 73 72 68

75 82 97 58 81 54 79 76 95 76

71 60 90 65 76 72 76 85 89 92

64 57 83 81 78 77 72 61 70 81

评分等级规定：60分以下为不及格；60─70分为及格；70─80分为中；80─90分为良,90─100分为优。

要求：

（1）将参加考试的学生按考试成绩分为不及格、及格、中、良、优五组并编制一张考核成绩次数分配表；

（2）指出分组标志及类型及采用的分组方法；

（3）计算学生物理课程考核平均成绩

（4）根据整理之后的统计变量序列，以95.45%的概率保证程度推断全体学生考试成绩的区间范围。

（5）若其它条件不变，将允许误差范围缩小一半，应抽取多少名学生的成绩？

解答：

首先，通过对学生物理课程考试的40个成绩进行分组统计，如下：

成绩	学生人数	频率（%）
60分以下	3	7.5
60-70分	6	15
70-80分	15	37.5
80-90分	12	30
90-100分	4	10
合计	40	100

对上面的表格进行变形，并进行计算：

成绩	组中值 $\large x$	学生人数 $\large f$	频率（%） $\large f/\sum f$	$\large \left ( x-\overline{x} \right )^{2}\times f$
60分以下	55	3	7.5	$\large \left ( 55-77.0 \right )^{2}\times 3= 1452$
60-70分	65	6	15	864
70-80分	75	15	37.5	60
80-90分	85	12	30	768
90-100分	95	4	10	1296
合计		40	100	4440

根据上表： $\large \sum f = 40$

根据计算公式：

$\large \overline{x} = \sum x \tfrac{f}{\sum f}$

从而得： $\large \overline{x}$ = 55×7.5%+65×15%+75×37.5%+85×30%+95×10% = 77.0

即学生物理课程考试成绩的平均值为：77.0分。

根据公式：

$\large \sigma = \sqrt{\sum \left ( x-\overline{x} \right )^{2}\times f/\sum f}$

从而得到： $\large \sigma = \sqrt{\frac{4440}{40}}= 10.54$

即该班级学生物理课程考试成绩的标准差为（ $\large \sigma = 10.54$ ）

进而， $\large \mu _{x} = \farc{\sigma }{\sqrt{n}}= 10.54 / \sqrt{40} = 1.67$

$\large \Delta _{x}= t\mu _x = 2\times 1.67 = 3.34$

全体学生考试成绩区间范围是：

下限 = $\large \overline{x} - \Delta _{x} = 77 - 3.34 = 73.66$

上限 = $\large \overline{x} + \Delta _{x} = 77 + 3.34 = 80.30$

即全体学生考生成绩区间范围在 73.66 —— 80.30 分之间。

如果将允许的误差范围缩小一半，则应抽取的学生人数为：

$\large n= \frac{t^{2}\sigma}{\Delta {x}^{2} } = \frac{2^{2} \times 10.54^{2}} {\left ( \frac{3.34}{2} \right )^{2}} \approx 159$

解答完毕。

第 2 题

有两个班级参加统计学考试，甲板的平均分数为75分，标准差11.5分；乙班的考试成绩资料如下：

按成绩分组（分）	学生人数（人）
60分以下	2
60-70分	5
70-80分	8
80-90分	6
90-100分	4
合计	25

要求：（1）计算乙班的平均分数和标准差；（2）比较哪个班级的平均分数更有代表性？

解答：

要计算乙班的平均分数，需要对上表进行一些简单的变形计算：

按成绩分组（分）	组中值（分） $\large \overline{x}$	学生人数（人） $\large f$	$\large \sum xf$
60分以下	55	2	110
60-70分	65	5	325
70-80分	75	8	600
80-90分	85	6	510
90-100分	95	4	380
合计		$\large \sum f = 25$	1925

乙班的平均成绩为：

$\large \overline{x} = \sum xf / \sum f = 1925 / 25 = 77.0$

根据公式：

$\large \sigma = \sqrt{\sum \left ( x-\overline{x} \right )^{2}\times f/\sum f}$

则： $\large \sigma = \sqrt{\frac{3400}{25}}= 11.66$

计算变异系数：

甲班： $\large \upsilon _{1} = \frac{\sigma }{\overline{x}} = 11.5 / 75 = 15.33$

乙班： $\large \upsilon _{2} = \frac{\sigma }{\overline{x}} = 11.66 / 77 = 15.14$

因为甲班级的标准差系数大于乙班级的标准差系数，所以乙班级的平均成绩更具有代表性。

第 3 题

某钢铁厂生产某种钢管，现从该厂某月生产的500根产品中抽取一个容量为100根的样本。已知一级品率为60%，试求样本一级品率的抽样平均误差。

求解：

由题意可知：一级品率为60%，即 p=60%；从500根产品中抽取一个容量为100根的样本，则： $\large N=500$ ， $\large n=100$ ，

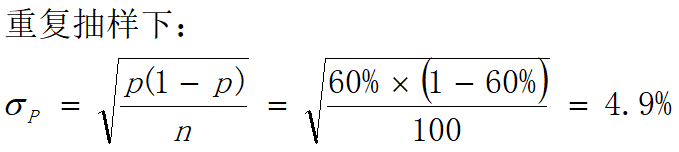
解答完毕。

第 4 题

某工厂生产的零件长度服从正态分布，从该工厂生产的零件中随机抽取25件，测得它们的平均长度为30.2厘米。已知总体标准差 $\large \sigma = 0.45$ 厘米。
求：（1）计算抽样平均误差和抽样允许误差。（2）估计零件平均长度的可能范围（ $\large \alpha = 0.05$ ）。

解答：

由题意可知 $\large X$ ~ $\large N\left ( \mu , 0.45^{2} \right )$ ， $\large \overline{X}=30.2$ ， $\large n=25$ ， $\large 1-\alpha =0.95$

（1）抽样平均误差为： $\large \sigma \left ( \overline{x} \right ) = \frac{\sigma }{\sqrt{n}} = \frac{0.45}{\sqrt{25}} = 0.09$ ，查标准正态分布表可知在 $\large \alpha =0.05$ 时， $\large z_{\alpha /2} = 1.96$ ，

所以抽样允许误差为： $\large \Delta _{\overline{x}} = z_{\alpha /2}\times \frac{\sigma }{\sqrt{n}} = 1.96\times 0.09 = 0.1764$

（2）总体均值的置信区间为：

$\large \left ( \overline{X}-\frac{\sigma }{\sqrt{n}}, \overline{X}+\frac{\sigma }{\sqrt{n}}\right ) = \left ( \overline{X}-\Delta _{\overline{X}},\overline{X}+\Delta _{\overline{X}} \right )$

即 $\large \left ( 30.2-0.1764,30.2+0.1764 \right ) =\left ( 30.02,30.38 \right )$

即我们可以以95%的概率保证该厂零件平均长度在30.02厘米到30.38厘米之间。

解答完毕。

第 5 题

从某市高中生中按不重复抽样方法随机抽取25名调查每周收看电视的时间，分组资料见表：

要求：（1）计算抽样平均误差和抽样允许误差；（2）估计该市全体高中生每周平均看电视时间的置信区间（给定的显著性水平为0.05）。

解答：根据题目意思首先将上表做一个简单的处理，

每周看电视时间（小时）	组中值 $\large x$	学生人数（人） $\large f$	$\large \left ( x-\overline{x} \right ) ^{2}\times f$
2以下	1	2	32
2 ~ 4	3	6	24
4 ~ 6	5	8	0
6 ~ 8	7	8	32
8 ~ 10	9	1	16
合计		$\large \sum f=25$	104

学生看电视的平均值为： $\large \overline{x} = \frac{1\times 2+3 \times 6 + 5 \times 8 + 7 \times 8 + 9 \times 1}{25} = 5$ 小时，

样本方差为： $\large \sigma ^{2}= 104/\left ( 25-1 \right )=4.33$

查 $\large t$ 分布表知 $\large \alpha =0.05$ 时，临界值 $\large t_{\alpha /2}\left ( n-1 \right ) = t_{\alpha /2}\left ( 25-1 \right ) = 2.0639$

因此：

抽样平均误差为： $\large \sigma \left ( \overline{X} \right ) = \frac{s}{\sqrt{n}} = \frac{\sqrt{4.33}}{\sqrt{25}} = 0.416$

抽样允许误差为： $\large \Delta _{\overline{X}} = t_{\alpha /2} \times \frac{s}{\sqrt{n}} = 2.0639 \times 0.416 = 0.859$

总体均值置信度为95%的置信区间为： $\large \left ( \overline{X}-\Delta _{\overline{X}},\overline{X}+\Delta _{\overline{X}} \right )$ ，即 $\large \left ( 5-0.859,5+0.859 \right ) = \left ( 4.14,5.86 \right )$

即我们可以以95%的把握保证该市高中生每周平均看电视时间在4.14到5.86小时之间。

解答完毕。

第 6 题

某工厂对一批产成品按不重复抽样方法随机抽选200件进行质量检测，其中一等品160件，试以90%的概率估计一等品率的范围。

解答：

由题意已知：p = 160/200 = 80%； 1-α = 90% ；n=200；

查表知： $\large z_{\alpha /2} = 1.645$ ，计算得样本比例的抽样平均误差为：

$\large \sigma \left ( p \right ) = \sqrt{\frac{p\times \left ( 1-p \right )}{n}} = \sqrt{\frac{0.8\times \left ( 1-0.8 \right )}{200}} = 0.0283$

抽样极限误差为： $\large \Delta _{p} = z_{\alpha /2}\times \sigma \left ( p \right ) = 1.645 \times 0.0283 = 0.04655$ ，即 4.655%

所以，该批产品的一等品比例的置信区间为：80%-4.655% ~ 80%+4.655%，即 75.35% ~ 84.66% 之间。

解答完毕。

第 7 题

从某班学生中随机抽取16人，计算得语文平均成绩为75分，方差为25分。假定学生成绩服从正态分布，试求总体方差及标准差的置信区间（给定的显著性水平为0.05）。

解答：

有题目已知： $\large n=25$ ， $\large \alpha =0.05$ ，查 $\large \chi ^{2}$ 分布表确定两个临界值：

$\large \chi_{1-\alpha /2}^{2} \left ( n-1 \right )= \chi _{0.975}^{2}\left ( 16-1 \right ) = 6.262$ ， $\large \chi_{\alpha /2}^{2} \left ( n-1 \right )= \chi _{0.025}^{2}\left ( 16-1 \right ) = 27.488$

将临界值数字带入公式中，总体方差和标准差的置信度为 $\large 1-\alpha$ 的置信区间分别为：

$\large \left (\frac{\left ( 16-1 \right ) \times 25}{27.488}, \frac{\left ( 16-1 \right ) \times 25}{6.262} \right )$ ，即 $\large \left ( 13.64,59.89 \right )$

$\large \left ( \sqrt{13.64},\sqrt{59.89} \right ) = \left ( 3.69,7.74 \right )$

解答完毕。

第 8 题

1、某快餐店某天随机抽取49名顾客对其的平均花费进行抽样调查。调查结果为：平均花费8.6元，标准差2.8 元。试以95.45％的置信度估计：
（1）该快餐店顾客总体平均花费的置信区间及这天营业额的置信区间（假定当天顾客有2000人）；
（2）若其他条件不变，要将置信度提高到99.73％，至少应该抽取多少顾客进行调查？

（提示： $\large z{_{0.0455}} = 1.69$ ， $\large z{_{0.0455/2}} = 2$ ， $\large z{_{0.0027/2}} = 3$ ， $\large z{_{0.0027}} = 2.78$ ）

解答：

由题意值 $\large \overline{x} = 8.6$ ，标准差： $\large \sigma = 2.8$ ， $\large n=49$ ，

则： $\large \mu _{\overline{x}} = \frac{\sigma }{\sqrt{n}} = 2.8 / \sqrt{49} = 0.4$

由于以95.45%的置信度估计，则 $\large 1-0.9545 = 0.0455$

$\large \Delta _{x} = z_{\alpha /2}\times \mu _{\overline{x}} = z_{0.0455/2} \times 0.4 = 2\times 0.4 = 0.8$

总体均值的置信区间： $\large \left ( 8.6-0.8 , 8.6+0.8 \right )$ ，即 $\large \left ( 7.8, 9.4 \right )$

营业总额的置信区间： $\large \left ( 2000\times 7.8, 2000\times 9.4 \right )$ ，即 $\large \left ( 15600, 18800 \right )$

若其它条件不变，将置信度提高到 99.73%，至少应该抽取的顾客数量为：

$\large 1- 0.9973 = 0.0027$

必要的样本容量： $\large n = \frac{z_{\alpha /2 \times \sigma ^{2}}} {\Delta_{\overline{x}}^{2}} = \frac{3^{2} \times 2.8 ^{2}}{0.8^{2}} = 110.25 \approx 111$

解答完毕。

第 9 题

一所大学准备采取一项学生在宿舍上网收费的措施，为了解男女学生对这一措施的看法，分别抽取了150名男学生和120名女学生进行调查，得到的结果如下：

	男学生	女学生	合计
赞成	45	42	87
反对	105	78	183
合计	150	120	270

请检验男女学生对上网收费的看法是否相同。已知：显著性水平 $\large \alpha =0.05$ ， $\large \chi_{0.05}^{2} \left ( 1 \right )= 3.842$ ， $\large \chi_{0.05}^{2} \left ( 2 \right )= 5.992$ ， $\large \chi_{0.05}^{2} \left ( 4 \right )= 9.487$ 。