统计学笔记（三）：统计量及其抽样分布

一、统计量

1.1 定义

设 $X_{1},X_{2},...,X_{n}$ 是从总体 $X$ 中抽取的容量为n的一个样本，如果由此样本构造一个函数 $T(X_{1},X_{2},...,X_{n})$ ，不依赖与任何未知参数，则成函数 $T(X_{1},X_{2},...,X_{n})$ 是一个统计量。

通常又称 $T(X_{1},X_{2},...,X_{n})$ 为样本统计量。当获得样本的一组具体观测值 $x_{1},x_{2},...,x_{n}$ ，代入 $T$ ，计算 $T(X_{1},X_{2},...,X_{n})$ 的数值，就获得一个具体的统计量值。

1.2 常用统计量

根据上述可知，统计量是样本的一个函数，不同的推断问题要求构造不同的统计量。要注意的是，依赖于总体分布的未知参数不属于统计量，比如数学期望 $E(X)$ 和方差 $D(X)$ 。

下列为常用的统计量：

样本均值： $\bar{X}=\frac{1}{n}\sum_{i=1}^{n}X_{i}$ ，反映出总体 $X$ 的数学期望。
样本方差： $S^{2}=\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\bar{X})^2$ ，反映的是总体 $X$ 方差的信息。
样本变异系数： $V=\frac{S}{\bar{X}}$ ，反映出随机变量在以它的均值为单位时取值的离散程度。
样本k阶矩： $m_{k}=\frac{1}{n}\sum_{i=1}^{n}X_{i}^{k}$ ，反映出总体k阶矩的信息。显然， $m_{1}=\bar{X}$ ，就是样本均值。
样本k阶中心矩： $v_{k}=\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\bar{X})^k$ ，反映了总体k阶中心矩的信息。显然， $v_{2}$ 就是样本方差。（数学期望和方差等概念可用“矩”的概念来描述）

二、统计三大分布

若对任一自然数n都能导出统计量 $T(X_{1},X_{2},...,X_{n})$ 的分布的数学表达式，这种分布成为精准的抽样分布。它对样本量n较小的统计推断问题非常有用。精准的抽样分布大多是在正态总体情况下得到的。在正态总条件下，主要有 $\chi ^{2}$ 分布、 $t$ 分布、 $F$ 分布，常称为统计三大分布。

2.1 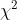$\chi ^{2}$ 分布

$\chi ^{2}$ 分布（Chi-squre distribution），就是卡方分布。定义如下：

设随机变量 $X_{1},X_{2},...,X_{n}$ 相互独立，且 $X_{i}(i=1,2,...,n)$ 服从标准正态分布 $N(0,1)$ ，则它们的平方和 $\sum_{i=1}^{n}X_{i}^{2}$ 服从自由度为 $n$ 的 $\chi ^{2}$ 分布。

自由度是统计学中常用的一个概念，它可以解释为独立变量的个数，还可以解释为二次型的秩。例如， $Y=X^{2}$ 是自由度为1的 $\chi ^{2}$ 分布， $rank(Y)=1$ ； $Z=\sum_{i=1}^{n}X_{i}^{2}$ 是自由度为 $n$ 的 $\chi ^{2}$ 分布， $rank(Z)=n$ 。

下图为当 $n=1$ ， $n=4$ ， $n=10$ ， $n=20$ 时， $\chi ^{2}$ 分布的概率密度函数曲线：

$\chi ^{2}$ 分布的数学期望为： $E(\chi ^{2})=n$ ； $\chi ^{2}$ 分布的方差为： $D(\chi ^{2})=2n$ ；

$\chi ^{2}$ 分布具有可加性，即若 $\chi _{1}^{2}\sim \chi^2(n_{1})$ ， $\chi _{2}^{2}\sim \chi^2(n_{1})$ ，且独立，则 $\chi _{1}^{2}+\chi _{2}^{2}\sim \chi ^{2}(n_{1}+n_{2})$ 。

由上图还可以看出，当自由度足够大时， $\chi ^{2}$ 分布的概率密度曲线趋于对称。当 $n\rightarrow +\infty$ 时， $\chi ^{2}$ 分布的极限分布时正态分布。

$\chi ^{2}(n)$ 的 $p$ 分位数 $\chi _{p}^{2}(n)$ 可由卡方分布表查得。当自由度 $n$ 很大时， $\sqrt{2\chi ^{2}(n)}$ 近似服从 $N(\sqrt{2n-1},1)$ 。实际上，当自由度 $n>45$ 时，有 $\chi _{p}^{2}(n)\approx \frac{1}{2}(\mu _{p}+\sqrt{2n-1})^2$ 。式中， $\mu _{p}$ 即 $Z _{p}$ ，为正态 $p$ 分位数，可由正态分布表查得。

卡方分布表：

2.2 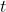$t$ 分布

$t$ 分布定义：

设随机变量 $X\sim N(0,1)$ ， $Y \sim \chi^2(n)$ ，且 $X$ 与 $Y$ 独立，则

$t=\frac{X}{\sqrt{Y/n}}$

其分布称为 $t$ 分布，记为 $t(n)$ ，其中 $n$ 为自由度。

$t$ 分布的概率函数是一偶函数，图形如下：

当 $n\geqslant 2$ 时， $t$ 分布的数学期望 $E(t)=0$ 。当 $n\geqslant 3$ 时， $t$ 分布的方差 $D(t)=\frac{n}{n-2}$ 。

由图可以看出， $t$ 分布的密度函数曲线与标准正态分布 $N(0,1)$ 的密度函数曲线非常相似，都是单峰偶函数，只是 $t(n)$ 的密度函数的两侧尾部要比 $N(0,1)$ 的两侧尾部粗一些。 $t(n)$ 的方差比 $N(0,1)$ 的方差大一些。

自由度为1的分布称为柯西分布，随着自由度 $n$ 的增加， $t$ 分布的密度函数越来越接近标准正态分布的密度函数。实际应用中，一般当 $n\geqslant 30$ 时， $t$ 分布与标准正态分布就非常接近了。

2.3 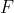$F$ 分布

$F$ 分布有着广泛的应用，在方差分析、回归方程的显著性检验中有着重要的地位。 $F$ 分布的定义：

设随机变量 $Y$ 和 $Z$ 相互独立，且 $Y$ 和 $Z$ 分别服从自由度为 $m$ 和 $n$ 的 $\chi ^{2}$ 分布，随机变量 $X$ 有如下表达式：

$X=\frac{Y/m}{Z/n}=\frac{nY}{mZ}$

则称 $X$ 服从第一自由度为 $m$ ，第二自由度为 $n$ 的 $F$ 分布，记为 $F(m,n)$ ，简记为 $X\sim F(m,n)$ 。

$F$ 分布的密度函数图如下图所示：

设随机变量 $X$ 服从 $F(m,n)$ 分布，则数学期望和方差分别为：

$E(X)=\frac{n}{n-2}$ ， $n>2$

$D(X)=\frac{2n^2(m+n-2)}{m(n-2)(n-4)}$ ， $n>4$

$F$ 分布的 $p$ 分位数 $F_{p}(v_{1},v_{2})$ 可查 $F$ 分布表获得，且 $F_{p}(v_{1},v_{2})=\frac{1}{F_{1-p}(v_{2},v_{1})}$

由此可知，在 $F$ 分布中，两个自由度的位置不可互换。此外，这一性质在查 $F$ 分布表时有重要应用。

$F$ 分布与 $t$ 分布还存在如下关系：

如果随机变量 $X$ 服从 $t(n)$ 分布，则 $X^2$ 服从 $F(1,n)$ 的 $F$ 分布。这在回归分析的回归系数显著性检验中有用。

三、中心极限定理

中心极限定理：

设从均值为 $\mu$ 、方差为 $\sigma ^2$ （有限）的任意一个总体中抽取样本量为 $n$ 的样本，当 $n$ 充分大时，样本均值 $\bar X$ 的抽样分布近似服从均值为 $\mu$ 、方差为 $\sigma ^2/n$ 的正态分布，即 $\bar X\sim N(\mu,\frac{\sigma ^2}{n})$ ，等价有 $\frac{\bar X-\mu}{\sigma /\sqrt{n}}\sim N(0,1)$ 。

注意： $\bar X$ 的期望值与总体均值相同，而方差则缩为总体方差的 $\frac{1}{n}$ 。这说明当用样本均值 $\bar X$ 去估计总体均值 $\mu$ 时，平均来说没有偏差（这一点称为无偏性）；当 $n$ 越来越大时， $\bar X$ 的散布程度越来越小，即用 $\bar X$ 估计 $\mu$ 就越来越准确。