线性代数 | (8) 线性方程组

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接： https://blog.csdn.net/sdu_hao/article/details/102736056

目录

1. 齐次线性方程组

2. 基础解系的求法

3. 非齐次线性方程组

4. 含参数的方程组

---

1. 齐次线性方程组

• 齐次线性方程组解的性质

• 齐次线性方程组解的性质

• 基础解系的求法

• 例题

2. 基础解系的求法

基础解系就是解空间中的一组基，通解是基础解系的线性组合。

• 基础解系的求法

接下来，自由未知量分别取如下向量：

然后可以分别得到真未知量的取值：

可以得到解空间的一组基础解系：

证明：首先可以知道是线性无关的，根据r维线性无关的向量组，增加n-r个分量，得到的n维向量组仍旧线性无关这一推论，后n-r个分量线性无关，所以增加r个分量组成的n维向量组也是线性无关的。

从推导过程可以看出:基础解系不惟一，但所含向量个数相等，都 等于 n - r(A). （n为未知量的个数或者系数矩阵的列数）。

• 定理

若齐次线性方程组的系数矩阵A的秩r(A)=r<n,则它有基础解系，且基础解系(解空间中的一组基)所含解向量的个数为n-r.

推论1:

• 例题

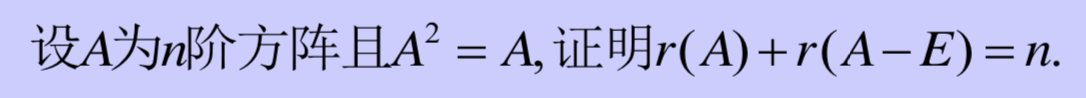
3. 非齐次线性方程组

• 非齐次线性方程组

• 非齐次线性方程组的有解判定

并非所有的非齐次线性方程组都有解，有解时，解的情况也不一样。

• 非齐次线性方程组的解法

• 例题

• 非齐次方程组的求解步骤

• 练习

4. 含参数的方程组

• 例题

当a=0时，系数矩阵的秩为1，基础解系包含的向量数 n-1；

当时， 系数矩阵的秩为n-1，基础解系包含的向量数 1；

注意例2不可以使用行列式求解，因为参数不在系数里，之前使用的行列式是系数行列式。