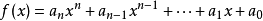文章目录
多项式简介
在数学中,由若干个单项式相加组成的代数式叫做多项式(若有减法:减一个数等于加上它的相反数)。多项式中的每个单项式叫做多项式的项,这些单项式中的最高项次数,就是这个多项式的次数。其中多项式中不含字母的项叫做常数项。
问题场景以及实现代码
问题描述:假设一个n次多项式
其中n是多项式的次数(即多项式中次数最高的项的次数),ai中存储指数为i的项的系数,x为多项式的自变量(为double类型),已知n和ai以及x的值,求多项式f(x)的值
问题分析:
定义double类型数组a[n+1],存放多项式系数ai,采用模块化编程,定义函数Polyf(double a[],int n,double x)求多项式的最终结果,下面代码分别定义了4个解决方法,分别讨论了不同算法的优劣。
这里假设求多项式f(x)=1+2x+3x^2,以下的分析基于该多项式
/*
假设求多项式f(x)=1+2x+3x^2
*/
#include <stdio.h>
#include <math.h>
#define N 3
const double x=1.1;//x的实际值
//数组a存放多项式系数,n为递多项式的次数,x为字母代数
double Polyf1(double a[],int n,double x);//调用库函数pow()
double Polyf2(double a[],int n,double x);//用循环语句求x^i
double Polyf3(double a[],int n,double x);//由迭代x^i=x^(i-1)*x,省略内层循环
double Polyf4(double a[],int n,double x);//采用秦九韶算法
int main(void)
{
double a[N]={1,2,3};
printf("Polyf1():1+2x+3x^2(x=1.1)=%lf\n",Polyf1(a,2,x));
printf("Polyf2():1+2x+3x^2(x=1.1)=%lf\n",Polyf2(a,2,x));
printf("Polyf3():1+2x+3x^2(x=1.1)=%lf\n",Polyf3(a,2,x));
printf("Polyf4():1+2x+3x^2(x=1.1)=%lf\n",Polyf4(a,2,x));
return 0;
}
double Polyf1(double a[],int n,double x)
{
double p=a[0],term;//根据假定要求,多项式第一项不带字母,不需要参与下面的计算 ,term存放x^i的值
for(int i=1;i<=n;i++)//n为多项式的次数(次数最高的项的次数,叫做这个多项式的次数。)
{
term=pow(x,i);//求x^i
p+=a[i]*term;
}
return p;
}
double Polyf2(double a[],int n,double x)
{
double p=a[0],term;
for(int i=1;i<=n;i++)
{
term=1;
for(int j=1;j<=i;j++)
{
term*=x;
}
// term=pow(x,i);
p+=a[i]*term;
}
return p;
}
double Polyf3(double a[],int n,double x)
{
double p=a[0];
double term=1;
for(int i=1;i<=n;i++)
{
term*=x;
p+=a[i]*term;
}
return p;
}
double Polyf4(double a[],int n,double x)
{
double p=a[n];
for(int i=n-1;i>=0;i--)
{
p=p*x+a[i];
}
return p;
}运行结果:
四种解决方法剖析
方法1:
double Polyf1(double a[],int n,double x)
{
double p=a[0],term;//根据假定要求,多项式第一项不带字母,不需要参与下面的计算 ,term存放x^i的值
for(int i=1;i<=n;i++)//n为多项式的次数(次数最高的项的次数,叫做这个多项式的次数。)
{
term=pow(x,i);//求x^i
p+=a[i]*term;
}
return p;
}
方法1分析:该方法调用头文件math.h中的double pow(double x,double i),求x的i次幂,最后再乘以系数a[i]得到多项式每一单项的值,当然,也可以自己写一个循环算法代替调用库函数,于是有了方法二
方法2:
double Polyf2(double a[],int n,double x)
{
double p=a[0],term;
for(int i=1;i<=n;i++)
{
term=1;
for(int j=1;j<=i;j++)
{
term*=x;
}
p+=a[i]*term;
}
return p;
}
方法1和方法2分析:方法1由于调用了库函数,所以效率稍微比方法2慢了一点,两者均是执行了1+2+…+n即3次乘法,n=2次加法,但如果设置的n过大,运行效率会很低
方法3:
double Polyf3(double a[],int n,double x)
{
double p=a[0];
double term=1;
for(int i=1;i<=n;i++)
{
term*=x;
p+=a[i]*term;
}
return p;
}
方法2和方法3分析:
由于方法2在(当i=2时)计算x^2的时候,要先计算1*x,然后再在x*(1*x),其实完全可以在i=1时,保留其值,然后再(当i=2时)直接利用i=1时计算的结果1*x,再乘以一个x,不需要重新计算1*x。即欲计算x^i,可用x^i=x^(i-1)*x迭代求出。修改的要点即要保留term变量计算完的值,然后可以省略内层循环。方法3函数共做了2n,即4次乘法,n=2次加法,当n较大时,由于x^i可以从前一个结果迭代算出,所以效率比方法2提高了一个数量级。
方法4:
double Polyf4(double a[],int n,double x)
{
double p=a[n];
for(int i=n-1;i>=0;i--)
{
p=p*x+a[i];
}
return p;
}
方法4分析:
采用秦九韶算法,秦九韶算法是一种将一元n次多项式的求值问题转化为n个一次式的算法。
如f(x)= 1+2x+3x^2 = 1+(2+3x)x
测试函数运行速度
所需头文件:“time.h”
所需函数:clock
函数原型:
clock_t clock( void );
这个函数返回从“开启这个程序进程”到“程序中调用clock()函数”时之间的CPU时钟计时单元(clock tick)
在time.h文件中,还定义了一个常量CLOCKS_PER_SEC,它用来表示一秒钟会有多少个时钟计时单元,其定义如下:
#define CLOCKS_PER_SEC ((clock_t)1000) //一秒=1000毫秒
clock函数返回进程运行时间,但是这个运行时间单位不是秒,而是CPU运行的时钟周期计数。
所以要得到消耗的时间(秒),需要除以CPU时钟频率,也就是CLOCKS_PER_SEC.以得到一个以秒为单位的数值。
/*
假设求多项式f(x)=1+2x+3x^2
*/
#include <stdio.h>
#include <math.h>
#include <time.h>
#define N 3
#define K 1e6
clock_t start, end;
double dur;
const double x=1.1;//x的实际值
double a[N]={1,2,3};
//数组a存放多项式系数,n为递多项式的次数,x为字母代数
double Polyf1(double a[],int n,double x);//调用库函数pow()
double Polyf2(double a[],int n,double x);//用循环语句求x^i
double Polyf3(double a[],int n,double x);//由迭代x^i=x^(i-1)*x,省略内层循环
double Polyf4(double a[],int n,double x);//采用秦九韶算法
void Ftick(double (*fp)(double *,int ,double));//测试函数的执行时间
int main(void)
{
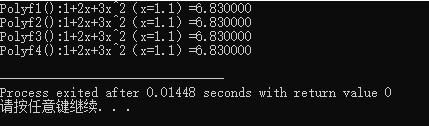
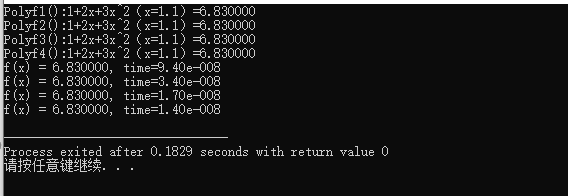
printf("Polyf1():1+2x+3x^2(x=1.1)=%lf\n",Polyf1(a,2,x));
printf("Polyf2():1+2x+3x^2(x=1.1)=%lf\n",Polyf2(a,2,x));
printf("Polyf3():1+2x+3x^2(x=1.1)=%lf\n",Polyf3(a,2,x));
printf("Polyf4():1+2x+3x^2(x=1.1)=%lf\n",Polyf4(a,2,x));
Ftick(Polyf1);
Ftick(Polyf2);
Ftick(Polyf3);
Ftick(Polyf4);
return 0;
}
double Polyf1(double a[],int n,double x)
{
double p=a[0],term;//根据假定要求,多项式第一项不带字母,不需要参与下面的计算 ,term存放x^i的值
for(int i=1;i<=n;i++)//n为多项式的次数(次数最高的项的次数,叫做这个多项式的次数。)
{
term=pow(x,i);//求x^i
p+=a[i]*term;
}
return p;
}
double Polyf2(double a[],int n,double x)
{
double p=a[0],term;
for(int i=1;i<=n;i++)
{
term=1;
for(int j=1;j<=i;j++)
{
term*=x;
}
// term=pow(x,i);
p+=a[i]*term;
}
return p;
}
double Polyf3(double a[],int n,double x)
{
double p=a[0];
double term=1;
for(int i=1;i<=n;i++)
{
term*=x;
p+=a[i]*term;
}
return p;
}
double Polyf4(double a[],int n,double x)
{
double p=a[n];
for(int i=n-1;i>=0;i--)
{
p=p*x+a[i];
}
return p;
}
void Ftick(double (*fp)(double *,int ,double))
{
double sum; //fp的返回值
start=clock(); //记录下面代码开始执行时的时钟打点数
for(int i = 1;i <= K;i++) //为了能测出时间,让函数fp执行K次
sum = fp(a, N, x);
end = clock(); //记录上面代码结束时的时钟打点数
dur=(double)(end - start) / CLK_TCK / K; //计算函数fp执行一次的时间(秒)
printf("f(x) = %f, time=%6.2e\n", sum, dur); //输出sum及dur
}执行结果:
可以发现最后一个方法的算法执行时间最短!
参考:《C语言从入门到项目实战》-----------王一萍等编著