注:
文章中所有的图片均来自台湾大学林轩田《机器学习基石》课程。
笔记原作者:红色石头
微信公众号:AI有道
上节课主要讲了为了避免overfitting,可以使用regularization方法来解决。在之前的\(E_{in}\)上加上一个regularizer,生成\(E_{aug}\),将其最小化,这样可以有效减少模型的复杂度,避免过拟合现象的发生。那么,机器学习领域还有许多选择,如何保证训练的模型具有良好的泛化能力?本节课将介绍一些概念和方法来解决这个选择性的问题。
一、Model Selection Problem
机器学习模型建立的过程中有许多选择,例如对于简单的二元分类问题,首先是算法\(\mathcal{A}\)的选择,有PLA,pocket,linear regression,logistic regression等等;其次是迭代次数\(T\)的选择,有100,1000,10000等等;之后是学习速率\(\eta\)的选择,有1, 0.01, 0.0001等等;接着是模型特征转换\(\Phi\)的选择,有linear,quadratic,poly-10,Legendre-poly-10等等;然后是正则化regularizer的选择,有L2,L1等等;最后是正则化系数\(\lambda\)的选择,有0,0.01,1等等。不同的选择搭配,有不同的机器学习效果。我们的目标就是找到最合适的选择搭配,得到一个好的\(g\),构建最佳的机器学习模型。

假设有\(M\)个模型,对应有\(\mathcal{H}_1,\mathcal{H}_2,...,\mathcal{H}_M\),即有\(M\)个hypothesis set,演算法为\(\mathcal{A}_1,\mathcal{A}_2,...,\mathcal{A}_M\),共\(M\)个。我们的目标是从这\(M\)个hypothesis set中选择一个模型\(\mathcal{H}_{m^*}\),通过演算法\(\mathcal{A}_{m^*}\)对样本集\(D\)的训练,得到一个最好的\(g_{m^*}\),使其\(E_{out}(g_{m^*})\)最小。所以,问题的关键就是机器学习中如何选择到最好的\(g_{m^*}\)。
考虑有这样一种方法,对\(M\)个模型分别计算使\(E_{in}\)最小的\(g\),再横向比较,取其中能使\(E_{in}\)最小的模型的\(g_{m^*}\):
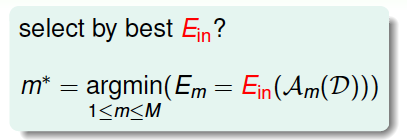
但是\(E_{in}\)足够小并不能表示模型好,反而可能表示训练的\(g_{m^*}\)发生了过拟合,泛化能力很差。而且这种“模型选择+学习训练”的过程,它的VC Dimension是\(d_{VC}(\mathcal{H}_1 \cup \mathcal{H}_2)\),模型复杂度增加。总的来说,泛化能力差,用\(E_{in}\)来选择模型是不好的。
另外一种方法,如果有这样一个独立于训练样本的测试集,将\(M\)个模型在测试集上进行测试,看一下\(E_{test}\)的大小,则选取\(E_{test}\)最小的模型作为最佳模型:

这种测试集验证的方法,根据finite-bin Hoffding不等式(有待回顾之前的内容),可以得到:\[E_{out}(g_{m^*})\leq E_{test}(g_{m^*})+O(\sqrt{\frac{logM}{N_{test}}})\] 由上式可以看出,模型个数\(M\)越少,测试集数目\(N_{test}\)越大,那么\(O(\sqrt{\frac{logM}{N_{test}}})\)越小,即\(E_{test}(g_{m^*})\)越接近于\(E_{out}(g_{m^*})\)。
下面比较一下之前讲的两种方法,第一种方法使用\(E_{in}\)作为判断基准,使用的数据集就是训练集\(D\)本身;第二种方法使用\(E_{test}\)作为判断基准,使用的是独立于训练集\(D\)之外的测试集。前者不仅使用\(D\)来训练不同的\(g_m\),而且又使用\(D\)来选择最好的\(g_{m^*}\),那么\(g_{m^*}\)对未知数据并不一定泛化能力好。举个例子,这相当于老师用学生做过的练习题再来对学生进行考试,那么即使学生得到高分,也不能说明他的学习能力强。所以最小化\(E_{in}\)的方法并不科学。而后者使用的是独立于\(D\)的测试集,相当于新的考试题能更好地反映学生的真实水平,所以最小化\(E_{test}\)更加理想。

但是,我们拿到的一般都是训练集\(D\),测试集是拿不到的。所以,寻找一种折中的办法,我们可以使用已有的训练集\(D\)来创造一个验证集validation set,即从\(D\)中划出一部分\(D_{val}\)作为验证集。\(D\)另外的部分作为训练模型使用, \(D_{val}\)独立开来,用来测试各个模型的好坏,最小化\(E_{val}\),从而选择最佳的\(g_{m^*}\)。

二、Validation
从训练集\(D\)中抽出一部分\(K\)个数据作为验证集\(D_{val}\), \(D_{val}\)对应的error记为\(E_{val}\)。这样做的一个前提是保证\(D_{val}\)独立同分布(iid)于\(P(x,y)\),也就是说\(D_{val}\)的选择是从\(D\)中平均随机抽样得到的,这样能够把\(E_{val}\)与\(E_{out}\)联系起来。\(D\)中去除\(D_{val}\)后的数据就是供模型选择的训练数据,其大小为\(N-K\)。从\(D_{train}\)中选择最好的\(g\),记为\(g^-_{m}\)。

假如\(D\)共有1000个样本,那么可以选择其中900个作为\(D_{train}\),剩下的100个作为\(D_{val}\)。使用\(D_{train}\)训练模型,得到最佳的\(g^-_m\),使用\(g^-_m\)对\(D_{val}\)进行验证,得到如下Hoffding不等式:\[E_{out}(g^-_m)\leq E_{val}(g_m^-)+O(\sqrt{\frac{logM}{K}})\] 假设有\(M\)种模型hypothesis set, \(D_{val}\)的数量为\(K\),那么从每种模型中得到一个在上\(D_{val}\)表现最好的\(g\) (还是在\(D_{train}\)上表现最好的\(g\)?),再横向比较,从\(M\)个\(g\)中选择一个最好\(m^*\)的作为我们最终得到的模型。
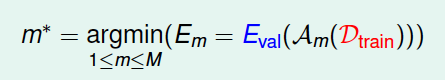
现在由于数量为\(N\)的总样本\(D\)的一部分\(K\)作为验证集,那么只有\(N-K\)个样本可供训练。从\(D_{train}\)中得到最好的\(g^-_{m^*}\),而总样本\(D\)对应的最好的\(g\)为\(g_{m^*}\)。根据之前的leraning curve很容易知道,训练样本越多,得到的模型越准确,其hypothesis越接近target function,即\(D\)的\(E_{out}\)比\(D_{train}\)的\(E_{out}\)要小:
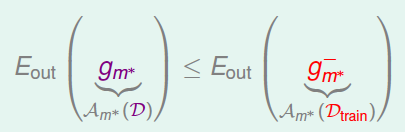
所以,我们通常的做法是通过\(D_{val}\)来选择最好的\(g^-_{m^*}\)对应的模型\(m^*\),再对整体样本集\(D\)使用该模型进行训练,最终得到最好的\(g_{m^*}\)。

总结一下,使用验证集进行模型选择的整个过程为:先将\(D\)分成两个部分,一个是训练样本\(D_{train}\),一个是验证集\(D_{val}\)。若有\(M\)个模型,那么分别对每个模型在\(D_{train}\)上进行训练,得到\(g_m^-\),再用\(D_{val}\)对每个\(g_m^-\)进行验证,选择表现最好的\(g^-_{m^*}\),则\(g^-_{m^*}\)对应的模型\(m^*\)被选择。最后使用该模型对整个\(D\)进行训练,得到最终的\(g_{m^*}\)。
不等式关系满足:\[E_{out}(g_{m^*})\leq E_{out}(g^-_{m^*})\leq E_{val}(g^-_{m^*})+O(\sqrt{\frac{logM}{K}})\] 下面举个例子来解释这种模型选择的方法的优越性,假设有两个模型:一个是5阶多项式\(H_{\Phi_5}\),一个是10阶多项式\(H_{\Phi_{10}}\)。通过不使用验证集和使用验证集两种方法对模型选择结果进行比较,分析结果如下:

图中,横坐标表示验证集数量\(K\),纵坐标表示\(E_{out}\)大小。黑色水平线表示没有验证集,完全使用\(E_{in}\)进行判断基准,那么\(H_{\Phi_{10}}\)更好一些,但是这种方法的\(E_{out}\)比较大,而且与\(K\)无关。黑色虚线表示测试集非常接近实际数据,这是一种理想的情况,其\(E_{out}\)很小,同样也与\(K\)无关,实际中很难得到这条虚线。红色曲线表示使用验证集,但是最终选取的是\(g^-_{m^*}\),其趋势是随着\(K\)的增加,它对应的\(E_{out}\)先减小再增大,当\(K\)大于一定值的时候,甚至会超过黑色水平线。蓝色曲线表示也使用验证集,最终选取的是\(g_{m^*}\),其趋势是随着\(K\)的增加,它对应的先缓慢减小再缓慢增大,且一直位于红色曲线和黑色直线之下。从此可见,蓝色曲线对应的方法最好,符合我们之前讨论的使用验证集进行模型选择效果最好。
这里提一点,当\(K\)大于一定的值时,红色曲线会超过黑色直线。这是因为随着\(K\)的增大,\(D_{val}\) 增大,但可供模型训练的\(D_{train}\)在减小,那得到的\(g^-_{m^*}\)不具有很好的泛化能力,即对应的\(E_{out}\)会增大,甚至当\(K\)增大到一定值时,比\(E_{in}\)模型更差。
那么,如何设置验证集\(K\)值的大小?根据之前的分析:
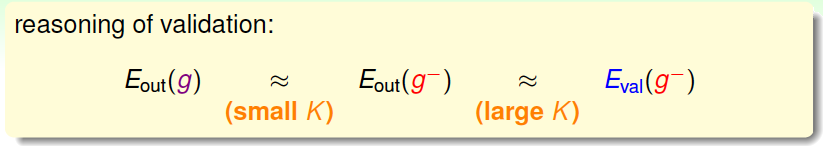
当\(K\)值很大时,\(E_{val}(g^-)\approx E_{out}(g^-)\) ,但是\(g^-_m\)与\(g_{m^*}\)相差很大;当\(K\)值很小时,\(g_m^-\approx g_{m^*}\) ,但是\(E_{val}(g^-)\)与\(E_{out}(g^-)\)可能相差很大。所以有个折中的办法,通常设置\(K=\frac{N}{5}\)。值得一提的是,划分验证集,通常并不会增加整体时间复杂度,反而会减少,因为\(D_{train}\)减少了。
三、Leave-One-Out Cross Validation
假如考虑一个极端的例子,\(K=1\),也就是说验证集大小为1,即每次只用一组数据对\(g^-_m\)进行验证。这样做的优点是\(g_m^-\approx g_{m^*}\),但是\(E_{val}\)与\(E_{out}\)可能相差很大。为了避免\(E_{val}\)与\(E_{out}\)相差很大,每次从\(D\)中取一组作为验证集,直到所有样本都作过验证集,共计算\(N\)次,最后对验证误差求平均,得到\(E_{loocv}(\mathcal{H},\mathcal{A})\),这种方法称之为留一法交叉验证,表达式为:\[E_{loocv}(\mathcal{H},\mathcal{A})=\frac{1}{N}\sum^N_{n=1} e_n=\frac{1}{N}\sum^N_{n=1} err(g^-_n(x_n,y_n))\] 这样求平均的目的是为了让\(E_{loocv}(\mathcal{H},\mathcal{A})\)尽可能地接近\(E_{out}(g)\)。
下面用一个例子图解留一法的过程:

如上图所示,要对二维平面上的三个点做拟合,上面三个图表示的是线性模型,下面三个图表示的是常数模型。对于两种模型,分别使用留一交叉验证法来计算\(E_{loocv}\),计算过程都是每次将一个点作为验证集,其他两个点作为训练集,最终将得到的验证误差求平均值,就得到了\(E_{loocv}(linear)\)和\(E_{loocv}(constant)\),比较两个值的大小,取值小对应的模型即为最佳模型。
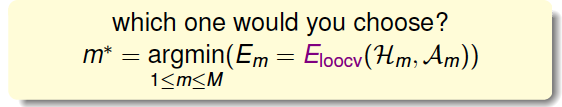
接下来,我们从理论上分析Leave-One-Out方法的可行性,即\(E_{loocv}(\mathcal{H},\mathcal{A})\)是否能保证\(E_{out}\)的\(g\)足够好?假设有不同的数据集\(D\),它的期望分布记为\(\epsilon_D\),则\(E_{loocv}(\mathcal{H},\mathcal{A})\)通过推导,等于\(E_{out}(N-1)\)的平均值。由于\(N-1\)近似为\(N\),\(E_{out}(N-1)\)的平均值也近似等于\(E_{out}(N)\)的平均值。具体推导过程如下:
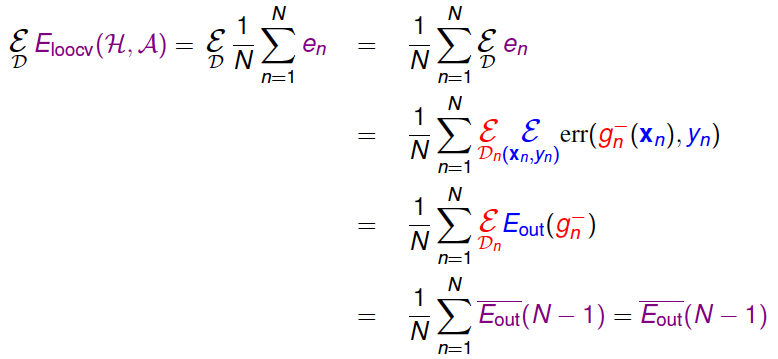
最终我们得到的结论是\(E_{loocv}(\mathcal{H},\mathcal{A})\)的期望值和\(E_{out}(g^-)\)的期望值是相近的,这代表得到了比较理想的\(E_{out}(g)\),Leave-One-Out方法是可行的。
举一个例子,使用两个特征:Average Intensity和Symmetry加上这两个特征的非线性变换(例如高阶项)来进行手写数字识别。平面特征分布如下图所示:
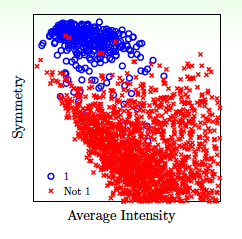
Error与特征数量的关系如下图所示:
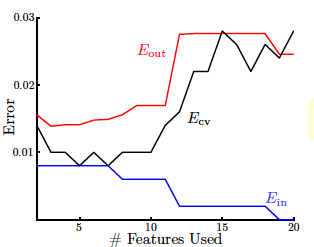
从图中我们看出,随着特征数量的增加, \(E_{in}\)不断减小, \(E_{out}\)先减小再增大,虽然\(E_{in}\)是不断减小的,但是它与\(E_{out}\)的差距越来越大,发生了过拟合,泛化能力太差。而\(E_{cv}\)与\(E_{out}\)的分布基本一致,能较好地反映\(E_{out}\)的变化。所以,我们只要使用Leave-One-Out方法得到使\(E_{cv}\)最小的模型,就能保证其\(E_{out}\)足够小。下图是分别使用\(E_{in}\)和\(E_{loocv}\)进行训练得到的分类曲线
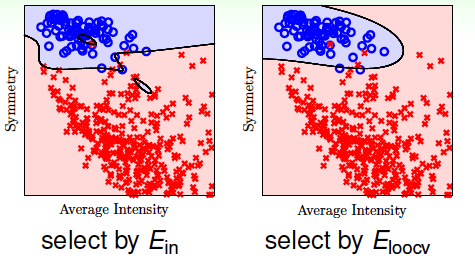
很明显可以看出,使用\(E_{in}\)发生了过拟合,而\(E_{loocv}\)分类效果更好,泛化能力强。
四、V-Fold Cross Validation
接下来我们看看Leave-One-Out可能的问题是什么。首先,第一个问题是计算量,假设\(N=1000\),那么就需要计算1000次的\(E_{loocv}\),再计算其平均值。当\(N\)很大的时候,计算量是巨大的,很耗费时间。第二个问题是稳定性,例如对于二分类问题,取值只有0和1两种,预测本身存在不稳定的因素,那么对所有的\(E_{loocv}\)计算平均值可能会带来很大的数值跳动,稳定性不好。所以,这两个因素决定了Leave-One-Out方法在实际中并不常用。
针对Leave-One-Out的缺点,对其作出了改进。Leave-One-Out是将\(N\)个数据分成\(N\)分,那么改进措施是将\(N\)个数据分成\(V\)份(例如\(V=10\)),计算过程与Leave-One-Out相似。这样可以减少总的计算量,又能进行交叉验证,得到最好的\(G\),这种方法称为V-折交叉验证。其实Leave-One-Out就是V-折交叉验证的一个极端例子。

一般的Validation使用V折交叉验证来选择最佳的模型。值得一提的是Validation的数据来源也是样本集中的,所以并不能保证交叉验证的效果好,它的模型一定好。只有样本数据越多,越广泛,那么Validation的结果越可信,其选择的模型泛化能力越强。
五、总结
本节课主要介绍了Validation验证。先从如何选择一个好的模型开始切入,例如使用\(E_{in}\)、\(E_{test}\)都是不太好的,最终使用\(E_{val}\)来进行模型选择。然后详细介绍了Validation的过程。最后,介绍了Leave-One-Out和V-Fold Cross两种验证方法,比较它们各自的优点和缺点,实际情况下,V-Fold Cross更加常用。