机器学习基石15：交叉验证（Cross Validation）

本文介绍了机器学习学习训练过程中的验证策略。包括留一法交叉验证和V-折交叉验证。

---

---

15.Validation

上节课介绍了抑制过拟合（overfitting）的方法–正则化（Regularization），通过引入正则化项，将最小化目标函数 $E_{in}$ 转化为 $E_{aug}$ ，限制高阶项的权重来减少模型复杂度，从而达到抑制过拟合的目的。还需要注意的一点是过拟合会导致模型泛化能力变差。一个模型有很多参数需要选择，那么应该如何选择模型参数使得模型具有良好的泛化能力呢？这是本节课介绍的内容。

15.1 Model Selection Problem

以二元分类为例，建模流程如下：

• 首先，选择算法 $A$ 。目前已经学习过的算法有：PLA， pocket，linear regression，logistic regression；
• 其次，设置迭代次数 $T$ 。比如：100，1000，10000。在实践过程中，一般常用的是epochs，即训练轮数（让算法看全部的训练样本多少轮）；
• 然后，设置学习率 $\eta$。常用的有：0.0001，0.01，0.1，1；
• 然后，选择模型特征转换函数 $\Phi$ 。常用的有：线性，二次多项式（ quadratic），十次多项式（poly-10），勒让德十次多项式（Legendre-poly-10）；
• 再然后，选择正则化方法 $\Omega(w)$。常用的有 L1正则化（稀疏正则化）和L2正则化（权重衰减正则化）；
• 最后，设置正则化项系数 $\lambda$ （拉格朗日乘子）。常用的有：0（不设置正则化），0.01，1。

根据以上规则设计模型时，基本上不可能一次设计就是完全满足自己业务需求的模型，还需要不断尝试不同的参数选择和模型组合，找到最好的矩 $g$ ，以此作为模型。（通过算法 $A$，选择一个最佳的假设（hypothesis）对应的函数称为 矩 $g$， $g$ 能最好地表示事物的内在规律，也是最终想要得到的模型表达式。）

---

接下来看模型选择问题。

假设有 $M$ 个模型（假设空间）： $H_1,H_2, . . . ,H_M$ ，每一个都有相对应的算法： $A_1,A_2, . . . ,A_M$。目标是从这 $M$ 个假设空间中选出一个 $H^{*}_m$ ，使用算法 $A^{*}_m$ 在数据集 $D$ 上训练，得到一个好的矩 $g^{*}_m$，使其 $E_{out}(g^{*}_m)$ 最小。问题的关键就是如何找到最好的矩 $g^{*}_m$。但是实际问题中，概率分布 $P(x)$ 和 $P(y|x)$ 是未知的，因此 $E_{out}$ 也是未知的。显然通过寻找最小的 $E_{out}$ 不可行。那么有没有其它可行的方法？

可以尝试对 $M$ 个模型分别计算使得 $E_{in}$ 最小的矩 $g$ ，再对比这些矩 $g$，取其中能使 $E_{in}$ 最小的 $g^{*}_m$ 对应的假设函数 $m^{*}$ 作为最终的模型。

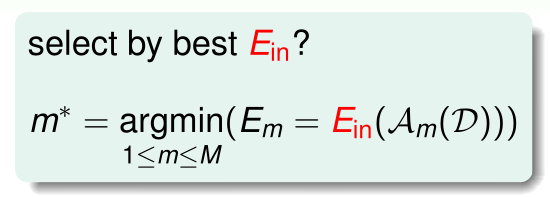
但是 $E_{in}$ 足够小，并不代表模型是最好的，因为可能存在过拟合。这种“选择模型+训练”的方式会导致 VC Dimention $d_{VC}(H_1∪H_2)$ 增大，从而使得模型复杂度增加，导致泛化性能变差。因此通过计算训练样本的 $E_{in}$ 来选择模型的策略也不合适。

既然训练样本不可行，那么可不可以考虑使用训练样本之外的数据，然后使用以上思路进行运算，最后再做选择？

在测试样本上对 $M$ 个模型分别计算使得 $E_{test}$ 最小的矩 $g$ ，再对比这些矩 $g$，选择使得 $E_{test}$ 最小的矩 $g^{*}_m$ 对应的假设函数 $m^{*}$ 即为最佳模型：

这种测试集验证的方法，根据霍夫丁不等式（finite­-bin Hoffding）不等式，可以得到：

在第七节课中讲到了该不等式，公式中 $O()$ 表示模型复杂度。由上式可知，若模型个数 $M$ 越少，且测试样本数量 $N_{test}$ 越大，则模型复杂度 $O$ 越小，即 $E_{test}$ 与 $E_{out}$ 越接近。但是目前这样做是不可行的，因为测试集是没有的。那么应该如何做？即我们熟知的，从训练集中划出一部分作为验证集，这就引出了下一小节的内容–验证（Validation）。

下面比较一下这三种策略：

第一种策略以 $E_{in}$ 作为判断基准，计算M个模型的使得 $E_{in}$ 最小的矩 $g$ 和从这 M 个矩 $g$ 中选出最优的矩 $g^{*}_m$ 的过程中，所使用的都是同样的数据训练样本 $D$，这就使得模型泛化能力不一定好（数据已经被模型学习过了，被“污染”了）。这相当于用平时做过的习题再出成试卷拿来考试，即使取得高分，也不能说明学习能力强。

第二种策略以 $E_{test}$ 作为判断基准，计算M个模型的使得 $E_{test}$ 最小的矩 $g$ 使用训练集样本，从这 M 个矩 $g$ 中选出最优的矩 $g^{*}_m$ 的过程中使用测试集样本，相当于平时用练习题，考试用题型相同但题目不一样的试卷进行考试，能更好的反应学生的学习能力。所以 $E_{test}$ 作为判断基准更合理。但是测试集是没有的，只有训练集 $D$。所以，寻找一种折中的办法，从已有的训练集 $D$ 中划出一部分 $D_{val}$ 作为验证集（validation set），其余部分当做训练集。这就是第三种策略。

第三种策略以 $E_{val}$作为判断基准，通过最小化 $E_{val}$ ，从而选择最优的矩 $g^{*}_m$ 。

---

习题1：

---

15.2 Validation

关于训练集和验证集的划分：在满足独立同分布（iid）的条件下， 从原来的包含 $N$ 个样本的数据集 $D$ （此处更正，之前的课程未提到验证集，一直称 $D$ 为训练样本，学已至此，这种称呼是不准确的，应该称为“数据集”更合适）中划分出一部分，作为验证集 $D_{val}$，其包含的样本数量为 $K$，其对应的误差即为 $E_{val}$。剩余的样本数据作为训练集 $D{trian}$ ，其包含的样本数量为 $N - K$，M个模型均使用 $D{trian}$ 训练得到的最优的矩 $g$，记为 $g^{-}_m$ 。

使用 $g^{-}_m$ 对 $D_{val}$ 进行验证，得到如下的霍夫丁不等式：

有了霍夫丁不等式保证，接下来需要根据最小化 $E_{val}$ 从 $M$ 个矩 $g$ 中选择最优的矩 $g^{-}_{m^{*}}$ 对应的假设函数 $m^{*}$ 作为最终的模型：

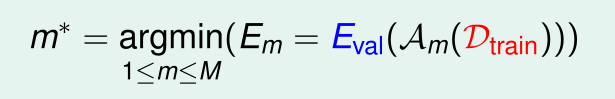
因为训练样本 $D_{trian}$ 得到的最优的矩 $g$ 为矩 $g^{-}_{m^{*}}$ ，总的样本 $D$ 得到的最优的矩 $g$ 为矩 $g_{m^{*}}$ ，由之前所学的学习曲线可知，训练样本越多，模型越精确，其假设函数越接近目标函数。即 $D$ 的 $E_{out}$ 要比 $D_{trian}$ 的 $E_{out}$ 要小得多。

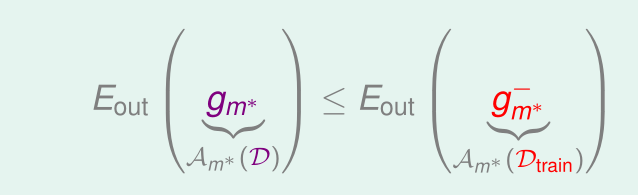
因此，常用做法是：以 $E_{train}$ 作为判断标准，M个模型分别在训练样本 $D_{trian}$ 上训练得到最优的矩 $g^{-}_m$ ；然后，以 $E_{val}$ 作为判断标准，在验证集 $D_{val}$ 上进行验证，即对比这 $M$ 个矩 $g^{-}_m$， 从中选出最优的矩 $g^{-}_{m^{*}}$ 对应的假设函数作为模型，使用该模型在总数据集 $D$ 上进行训练，得到最终的 $g_{m^{*}}$ 。算法计算思路和模型选择流程图如下所示：

下面通过一个例子直观地说明这种模型选择方法的优越性。使用交叉验证从五阶多项式假设空间到十阶多项式假设空间之间选择一个模型，做对比如下 ：

左图信息说明：

• 横轴：验证集包含的样本数 $K$；
• 纵轴：预测输出的误差 $E_{out}$；
• 黑线：不划分验证集，直接使用整个数据集训练得到的最优的矩 $g_{\hat{m}}$；
• 红线：划分验证集，以 $E_{train}$ 作为判断标准，M个模型分别在训练样本 $D_{trian}$ 上训练得到最优的矩 $g^{-}_m$ ；然后，以 $E_{val}$ 作为判断标准，在验证集 $D_{val}$ 上进行验证，即对比这 $M$ 个矩 $g^{-}_m$， 从中选出最优的矩 $g^{-}_{m^{*}}$ ；
• 蓝线：更进一步，使用矩 $g^{-}_{m^{*}}$ 对应的假设函数作为模型，在总数据集 $D$ 上进行训练，得到最终的 $g_{m^{*}}$ 。

由以上可知， $E_{out}(g_{m^{*}}) ≤ E_{out}(g^{-}_{m∗})$ ，蓝色线所代表的策略选出的模型性能更好。当验证集样本数量 $K$ 大于一定的值时，红线会超过黑线。这是因为随着验证集样本数量 $K$ 的增大，训练集样本数量 $N-K$ 减少，得到的假设函数（模型）越来越差，即对应的 $E_{out}$ 会增大，当 $K$ 继续增大时，比在整个数据集上训练得到的模型更差。

关于验证集样本数量 $K$ 的选择问题：

当验证集样本数量 $K$ 很大时， $E_{val}(g^{-}) \approx E_{out}(g^{-})$ ，但因为训练集样本数量 $N-K$ 减少，导致 $E_{out}(g)$ 与 $E_{out}(g^{-})$ 相差很大；当 $K$ 比较小时， $E_{out}(g) \approx E_{out}(g^{-})$，但 $E_{val}(g^{-})$ 与 $E_{out}(g^{-})$ 相差很大。所以有个折中的办法，通常设置 $K = \frac{N}{5}$ 。划分验证集，通常会减少时间复杂度，因为 $D_{train}$ 变小了。

---

习题2：

---

15.3 Leave-One-Out Cross Validation

上小节提到了验证集，先考虑一个极端的例子，每次将数据集 $D$ 中的一个样本（ $K$ = 1）作为验证集来求解矩 $g_n$ ，即验证集 $D^{(n)}_{val} = \{(x_n,y_n) \}$ 。这种方法的缺点是 $E_{val}$ 与 $E_{out}$ 可能相差很大。为了减小 $E_{val}$ 与 $E_{out}$ 之间的差距，引入留一法交叉验证（Leave-One-Out Cross Validation）。

顾名思义，留一法交叉验证，即每次从数据集 $D$ 中取一个样本作为验证集，直到所有样本都做过验证集，共计算 $N$ 次，最后对验证误差求平均，得到 $E_{loocv}(H,A)$：

这样做的目的使使得 $E_{loocv}(H,A) ≈ E_{out}(g)$。

下面通过一个直观的例子说明留一法交叉验证。分别使用线性模型和常数模型对二维平面上的三个样本点做拟合，使用留一法交叉验证。这两种模型对应的 $E_{loocv}(H,A)$ 求解结果如下：

每次将一个样本点作为验证集，其他两个样本点作为训练集，最后将得到的验证误差求平均值，得到 $E_{loocv}(linear)$ 和 $E_{loocv}(constant)$，值较小的 $E_{loocv}$ 所对应的模型即为最佳模型。

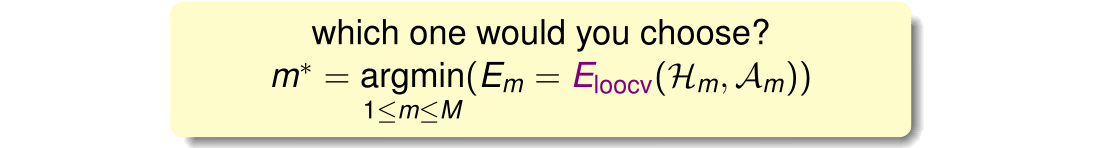
由此可知，常数模型比线性模型错误率更低，因为复杂度更低。那么 $E_{loocv}(H,A)$ 与 总体平均的 $E_{out}(g)$ 近似吗？下面从理论的角度证明 $E_{loocv}(H,A)$ 与总体平均 $E_{out}(g)$ 的关系。假设有不同的数据集 $D$，其期望分布为 $\varepsilon_D$。

由以上分析可知， $E_{loocv}(H,A)$ 与 总体平均的 $E_{out}(g)$ 近似，这表示留一法交叉验证是可行的。下例通过手写数字识别进行说明：

蓝色表示数字"1"的样本，红色表示数字"1"之外的样本，以对称性（symmetry）和密度（intensity）为样本的特征值，中间的图为以 $E_{in}$ 作为优化目标求出的分类超平面，很不平滑；右图为以 $E_{loocv}(H,A)$ 作为优化目标求出的分类超平面，平滑很多。绘制特征数量与误差之间的关系曲线：

从图中不难得出，随着特征数增多（模型复杂度提高）， $E_{in}$ 不断降低（高阶多项式拟合能力强）， $E_{out}$ 不断增加。 $E_{in}$ 与 $E_{out}$ 相差越来越大；而 $E_{cv}$ 和 $E_{out}$ 的曲线非常接近。因此 $E_{cv}$ 比 $E_{in}$ 分类效果好，泛化能力强。

---

习题3：

---

15.4 V-Fold Cross Validation

上一节中介绍的留一法交叉验证存在两个问题：一是数据量比较大时，选择模型的计算开销很大，比如样本为1000个，则每个模型要使用999个样本运行1000次；二是稳定性不好，因为总是单一样本做验证，导致 $E_{cv}$ 的曲线波动，很不稳定。实际应用中很少使用留一法交叉验证。

为了解决留一法交叉验证的两个问题，提出了V­折交叉验证（V-Fold Cross Validation），将样本数据集分成大小相等的V个子集，每次随机选择其中V-1个子集作为训练集，一个子集作为验证集。留一法交叉验证是V­折交叉验证的一个极端例子。

常用V­折交叉验证选择最佳的模型。因为验证集的样本是样本集中的一部分，所以并不能保证交叉验证的效果好，其模型一定好。只有样本数据足够丰富，交叉验证的结果才越可信，其选择的模型泛化能力越强。

---

习题4：

---

Summary

本节课主要介绍了机器学习训练过程中的验证方法。从模型选择引入问题，经过分析可知，使用 $E_{in}$ 或者 $E_{test}$ 都存在很大的问题，于是使用 $E_{val}$ 作为评价指标。然后详细介绍了验证的过程。最后介绍留一法交叉验证和 V-折交叉验证的原理及其优缺点。实际应用时，使用V-折交叉验证，通常取V=10。

---

参考
https://www.cnblogs.com/ymingjingr/p/4306666.html
https://github.com/RedstoneWill/HsuanTienLin_MachineLearning