Lecture 14:Regularization
Regularized Hypothesis Set
当训练样本数不够多,而假设函数次数比较高时,很容易发生过拟合,正则化的目的就是希望让高维的假设函数退化成低维的假设函数
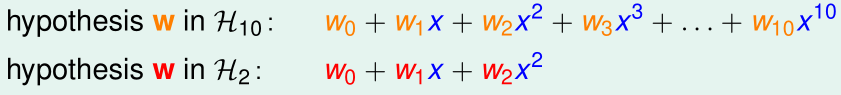
如上图,高维假设函数的参数里,高阶项对应的参数(w3,...,w10)就都被限制为0了
如果我们希望把\(\mathcal H_{10}\)退化为\(\mathcal H_{2}\),加正则化的优化目标变成了:
\[\arg \min_{w\in \mathbb R^{10+1}} E_{in}(w)\]
\[\mathrm{s.t.}\ \ w_3=\cdots=w_{10}=0\]
这样做看起来是多此一举,直接用\(\mathcal H_2\)不就好了?实际上这是为后面的工作作铺垫。
现在我们要对这个优化目标的约束条件放宽一点:
\[\arg \min_{w\in \mathbb R^{10+1}} E_{in}(w)\]
\[\mathrm{s.t.}\ \ \sum_{i=0}^{10}1\{w_i\neq 0\}\leq 3\]
(约束条件放宽为,11个参数项里最多有3个不为0)
这个优化目标比之前的约束条件更宽松,但比没加约束的优化目标,发生过拟合的概率更低。
然而,求解这个优化目标是NP-Hard的,我们需要进一步将它的约束条件变成"软"约束:
\[\arg \min_{w\in \mathbb R^{10+1}} E_{in}(w)\ \ \mathrm{s.t.}\ \ \sum_{i=0}^{10} w_i^2\leq C\]
(注意,这个优化目标与上一个优化目标不是完全等价的)
约束条件可以看作是\(w^Tw\leq C\),C就是向量W的最大长度,约束边界可以看作是一个超球面,C越大,表明对参数的限制越宽松。
Weight Decay Regularization
我们用矩阵形式重写上面的优化目标:
\[\arg \min_{w\in \mathbb R^{Q+1}} E_{in}(w)=\frac 1 n (Zw-y)^T(Zw-y)\]
\[\mathrm{s.t.}\ \ w^Tw\leq C\]
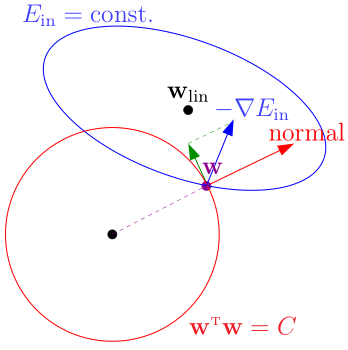
优化过程中,\(w\)沿\(-\nabla_w E_{in}\)的方向不断走,直到到达约束边界\(w^Tw=C\)
此时仍有优化的余地,为了不违反约束条件,我们把\(-\nabla_w E_{in}\)分解为两个分量:
- 红色向量(边界的法线方向)
- 绿色向量(边界的切线方向)
此时,我们保留绿色的分量,让w沿着绿色分量的方向走,直到绿色分量为0(即\(-\nabla_w E_{in}\)与红色向量平行),表明到达了在约束条件下的最优点
有了几何上的直观理解后,我们就知道了,在这个约束条件下,最优点\(w_{REG}\)的条件是\(-\nabla_w E_{in}(w_{REG})\)与红色向量(方向为\(w_{REG}\))平行:
\[\nabla_w E_{in}(w_{REG})=kw_{REG}\]
改写为:
\[\nabla_w E_{in}(w_{REG})+\frac{2\lambda} n w_{REG}=0\]
\(\lambda\)被称为拉格朗日乘子
现在,我们的任务是求出\(w_{REG}\)
\[E_{in}(w)=\frac 1 n (Zw-y)^T(Zw-y)\]
\[\nabla_w E_{in}=\frac 2 n (Z^TZw-Z^Ty)\]
\[\frac 2 n (Z^TZw_{REG}-Z^Ty)+\frac {2\lambda} n w_{REG}=0\]
\[w_{REG}=(Z^TZ+\lambda I)^{-1}Z^Ty\]
其中,\(Z^TZ\)是半正定的,如果\(\lambda >0\),则\(\lambda I\)是正定的,\(Z^TZ+\lambda I\)也就是正定的,进一步可以推出\(Z^TZ+\lambda I\)一定可逆
上述的线性回归被称为Ridge Regression(岭回归)
下面,我们把正则化推广到更一般的情况
\(\nabla_w E_{in}(w_{REG})\)是\(E_{in}(w)\)对w的导数,\(\frac{2\lambda} n w_{REG}\)是\(\frac{\lambda} n w^Tw\)对w的导数,满足\(\nabla_w E_{in}(w_{REG})+\frac{2\lambda} n w_{REG}=0\)的点\(w_{REG}\)可以使\(E_{in}(w)+\frac \lambda n w^Tw\)取得极小值
于是问题可以看作是最小化\(E_{aug}(w)=E_{in}(w)+\frac \lambda n w^Tw\),其中第二项就是正则化项(regularizer),我们称\(E_{aug}(w)\)为增广误差(augmented error)