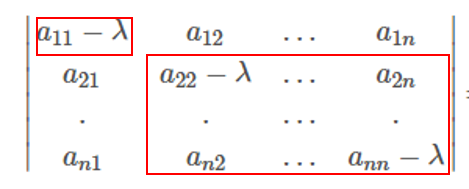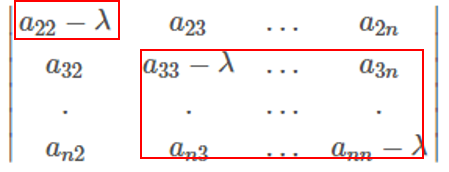矩阵的迹trace相关问题的证明

申明：仅个人小记

要证明的内容具体为：

(1) 方阵A的主对角线之和等于所有特征值之和，主对角线之和称之为矩阵的迹(trace)。
(2) 方阵A对应的行列式值等于所有特征值之积。

一、求特征值的方法

能够使得方阵A满足 $A\vec{x}=\lambda\vec{x}$ 的 $\lambda$ 称之为特征值， $\vec{x}$ 称之为特征向量 （其中 $\vec{x}$ 要求为非零向量，如果是零向量则没有讨论的意义）。

A \vec{x} = λ \vec{x} \to (A - λ) \vec{x} = \vec{0}

$A\vec{x}=\lambda\vec{x}\rightarrow(A-\lambda)\vec{x}=\vec{0}$
注意到

(A - λ) \vec{x} = \vec{0}

$(A-\lambda)\vec{x}=\vec{0}$ 是齐次线性方程组，所以求特征向量的问题就转变为求这个齐次线性方程组的非零解的问题。
{
而已知，对于一个齐次线性方程组

A \vec{x} = \vec{0}

$A\vec{x}=\vec{0}$ 来说，当矩阵A满秩，那么这个齐次线性方程组只能有一个零解，而不存在其他的解。所以，要想得到非零解，必须得满足

r (A) < n

$r(A)<n$ 即,

| A | = 0

$\left |A\right |=0$
}

所以，要想让 $(A-\lambda)\vec{x}=\vec{0}$ 有非零解，则必须满足

| A - λ | = 0

$\left | A-\lambda \right |=0$

二、寻找 ${\lambda}^{n-1}$ 项的系数的第一个方案

将 $\left |A\right |=0$ 展开，即为

| \begin{matrix} a_{11} - λ & a_{12} & . . . & a_{1 n} \\ a_{21} & a_{22} - λ & . . . & a_{2 n} \\ . & . & . . . & . \\ a_{n 1} & a_{n 2} & . . . & a_{n n} - λ \end{matrix} | = 0

$\begin {vmatrix} a_{11}-\lambda&a_{12} &...&a_{1n}\\a_{21}&a_{22}-\lambda&...&a_{2n}\\.&.&... &.\\a_{n1}&a_{n2}&...&a_{nn}-\lambda\end {vmatrix}=0$

根据拉普拉斯定理对其按第一行展开

(a_{11} - λ) A_{11} + a_{12} A_{12} + . . . + a_{1 n} A_{1 n} = 0

$(a_{11}-\lambda)A_{11}+a_{12}A_{12}+...+a_{1n}A_{1n}=0$
我们可以知道，在这个方程中，未知数是

λ

$\lambda$ ，这个方程中未知数

λ

$\lambda$ 的最高阶数为n，并且我们可以看出，在这个等式中

λ^{n}

${\lambda}^{n}$ 项和

λ^{n - 1}

${\lambda}^{n-1}$ 项 只有可能出现在

(a_{11} - λ) A_{11}

${(a_{11}-\lambda)}A_{11}$ 中，如下图示意，

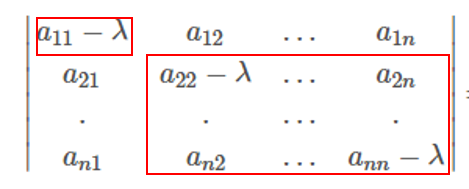
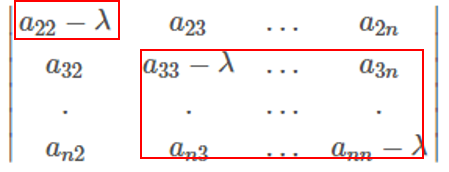
所以，最终含有

λ^{n}

${\lambda}^{n}$ 项和

λ^{n - 1}

${\lambda}^{n-1}$ 项的式子为

(a_{11} - λ) (a_{22} - λ) . . . (a_{22} - λ)

$(a_{11}-\lambda)(a_{22}-\lambda)...(a_{22}-\lambda)$ 方案一的结论
所以根据代数定理，我们可以知道

λ^{n - 1}

${\lambda}^{n-1}$ 的系数为

a_{11} + a_{22} . . . + a_{n n}

$a_{11}+a_{22}...+a_{nn}$ ，即主对角线之和，即矩阵

A - λ

$A-\lambda$ 的迹。

三、寻找 ${\lambda}^{n-1}$ 项的系数的第二个方案

我们知道A必然存在n个特征值(重根算数，复根也算数)，记方阵A的n个特征值为 $\lambda_1,\lambda_2,...,\lambda_n$ ，则可知 $\left | A-\lambda\right |=0$ 必然可以化为

(λ - λ_{1}) (λ - λ_{2}) . . . (λ - λ_{n}) = 0

$(\lambda -\lambda_1)(\lambda-\lambda_2)...(\lambda-\lambda_n)=0$
方案二的结论
根据代数定理容易知道，
(1)、该方程的

λ^{n - 1}

${\lambda}^{n-1}$ 项的系数为

λ_{1} + λ_{2} + . . . + λ_{n}

$\lambda_1+\lambda_2+...+\lambda_n$ ;
(2)、当

λ = 0

$\lambda=0$ 时，

| A | = | A - 0 | = (0 - λ_{1}) (0 - λ_{2}) . . . (0 - λ_{n}) = λ_{1} λ_{2} . . . λ_{n}

$\left|A\right|=\left | A-0 \right |=(0-\lambda_1)(0-\lambda_2)...(0-\lambda_n)=\lambda_1\lambda_2...\lambda_n$

当方阵A的阶数n为奇数时，必然 $\left | A-\lambda \right |$ 中 ${\lambda}^{n}$ 项的系数为-1。此时应有

| A - λ | = - 1 * (λ - λ_{1}) (λ - λ_{2}) . . . (λ - λ_{n})

$\left | A-\lambda \right |=-1*(\lambda -\lambda_1)(\lambda - \lambda_2)...(\lambda - \lambda_n)$ 当方阵A的阶数n为偶数时，必然

| A - λ |

$\left | A-\lambda \right |$ 中

λ^{n}

${\lambda}^{n}$ 项的系数为1。此时应有

| A - λ | = (λ - λ_{1}) (λ - λ_{2}) . . . (λ - λ_{n})

$\left | A-\lambda \right |=(\lambda -\lambda_1)(\lambda - \lambda_2)...(\lambda - \lambda_n)$
可知，当

λ = 0

$\lambda=0$ 时，恒有

| A | = | A - 0 | = λ_{1} λ_{2} . . . λ_{n}

$\left|A\right|=\left | A-0 \right |=\lambda_1\lambda_2...\lambda_n$
即，特征值之积等于行列式的值，证毕。

结合方案一和方案二的结论可知， ${\lambda}^{n-1}$ 项的系数为

a_{11} + a_{22} + . . . + a_{n n} = λ_{1} + λ_{2} + . . . + λ_{n}

$a_{11}+a_{22}+...+a_{nn}=\lambda_1+\lambda_2+...+\lambda_n$
即，主对角线之和等于特征值之和，证毕。