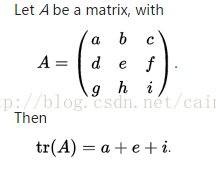在学习andrew ng的深度学习公开课里,可看到一段与数据的矩阵相关的,这里提出了求trace的算法以及规则,虽然学习过高数,线代,概率论,还有数理方程等等,但还是没有什么印象,一脸迷茫。这段相关的文本,我放到这里,如下:
只能先百度一下:
在线性代数中,一个n×n的对角矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数),一般记作tr(A)。
例子如下:
对角元素是a,e,i,这三者之和就叫矩阵的迹。
我一直在想,为什么非要抓住这个矩阵的对角线不放呢?难道有什么高深的学问吗?
后来仔细一想,矩阵的对角线可以表示一个物体的相似性,比如在图形学的缩放变换里使用的矩阵是这样的:
在这里可以看到就是对角的元素表示缩放,那么表示物体具有相似性。
在机器学习里,主要为了获取数据的特征值,那么就是说,在任何一个矩阵计算出来之后,都可以简单化,只要获取矩阵的迹,就可以表示这一块数据的最重要的特征了,这样就可以把很多无关紧要的数据删除掉,达到简化数据,提高处理速度。
百度百科中完整的关于矩阵的迹的性质的介绍:
(1)设有N阶矩阵A,那么矩阵A的迹(用

表示)就等于A的特征值的总和,也即矩阵A的主对角线元素的总和。
1.迹是所有对角元的和
2.迹是所有特征值的和
3.某些时候也利用tr(AB)=tr(BA)来求迹
4.trace(mA+nB)=m trace(A)+n trace(B)
(2)奇异值分解(Singular value decomposition )
奇异值分解非常有用,对于矩阵A(p*q),存在U(p*p),V(q*q),B(p*q)(由对角阵与增广行或列组成),满足A = U*B*V
U和V中分别是A的奇异向量,而B是A的奇异值。AA'的特征向量组成U,特征值组成B'B,A'A的特征向量组成V,特征值(与AA'相同)组成BB'。因此,奇异值分解和特征值问题紧密联系。
如果A是复矩阵,B中的奇异值仍然是实数。
SVD提供了一些关于A的信息,例如非零奇异值的数目(B的阶数)和A的阶数相同,一旦阶数确定,那么U的前k列构成了A的列向量空间的正交基。
(3)在数值分析中,由于数值计算误差,测量误差,噪声以及病态矩阵,零奇异值通常显示为很小的数目。
将一个矩阵分解为比较简单或者性质比较熟悉的矩阵之组合,方便讨论和计算。由于矩阵的特征值和特征向量在化矩阵为对角形的问题中占有特殊位置, 因此矩阵的特征值分解。尽管矩阵的特征值具有非常好的性质,但是并不是总能正确地表示矩阵的“大小”。矩阵的奇异值和按奇异值分解是矩阵理论和应用中十分重要的内容,已成为多变量反馈控制系统最重要最基本的分析工具之一,奇异值实际上是复数标量绝对值概念的推广, 表示了反馈控制系统的输出/输入增益,能反映控制系统的特性。《鲁棒控制.倾斜转弯导弹》
关于迹的证明,可以看这里: