买不到的数目
小明开了一家糖果店。他别出心裁:把水果糖包成4颗一包和7颗一包的两种。糖果不能拆包卖。
小朋友来买糖的时候,他就用这两种包装来组合。当然有些糖果数目是无法组合出来的,比如要买 10 颗糖。
你可以用计算机测试一下,在这种包装情况下,最大不能买到的数量是17。大于17的任何数字都可以用4和7组合出来。
本题的要求就是在已知两个包装的数量时,求最大不能组合出的数字。
输入:
两个正整数,表示每种包装中糖的颗数(都不多于1000)
要求输出:
一个正整数,表示最大不能买到的糖数
不需要考虑无解的情况
例如:
用户输入:
4 7
程序应该输出:
17
再例如:
用户输入:
3 5
程序应该输出:
7
资源约定:
峰值内存消耗 < 64M
CPU消耗 < 3000ms
观察题目,其实可以把题目抽象成:有两个正整数a、b,可以组成任意线性组合ax+by,x、y非负,求最大不能组合数。
我们可以证明这两个数一定互质。设ax+by=c,如果a、b不互质,则gcd(a,b)≠0,a、b的线性组合一定是gcd(a,b)的倍数;当c的取值不是gcd(a,b)的倍数时,方程无解,此时a、b不能组合数无上界(只要不是gcd(a,b)的倍数都无法组合,这样的数有无数多个),所以a、b一定互质(即gcd(a,b)=1)。
法一:
做这道题有一个结论可以直接用:两个互质数a、b的最大不能组合数为ab-a-b。下面给出详细证明(参考):
如果有离散数学的基础,我们知道可以把所有非负整数划分成a个模a同余等价类,记为[0],[1],[2],...,[a-1],分别为ak,ak+1,ak+2,…,ak+(a-1),(k∈Z)。b的倍数一定分布在这a个等价类中,又因为gcd(a,b)=1,所以每个等价类中都有b的倍数,且均分分布(这边想不通可以自己取两个数比画一下,就很好理解了)。特别的,ab∈[0]。设bKi是等价类[i]中最小的b的倍数,那么该等价类中bKi后的所有数都能表示成ax+bKi,一定能被组合出来。显然,最大的bKi后面的所有连续整数都可以被组合出来,而要找到最大不能组合数,我们只需考虑最大的bKi前面的数字即可。把所有的bKi列出来,有{0,b,2b,...,(a-1)b}。很显然(a-1)b就是最大的bKi,而在其他a-1个等价类中,必定有比它小且能被组合的数,这些数就是(a-1)b-1,(a-1)b-2,...,(a-1)b-(a-1)。所以最大不能被组合数就是(a-1)b-a,即ab-a-b。
为了便于理解,我以4、7为例画了个图表,结合图表应该很容易就能看懂上面的证明过程:
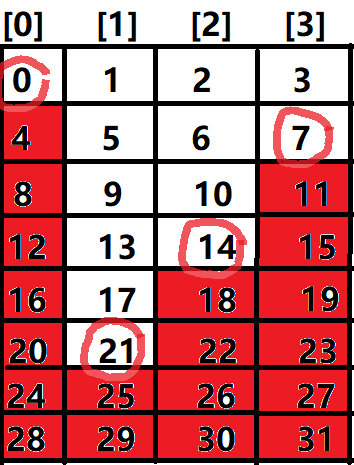
知道了这个结论,这道题就很好做了,几乎是水过:

1 #include<iostream> 2 using namespace std; 3 4 int main(){ 5 int a,b; 6 cin>>a>>b; 7 cout<<a*b-a-b<<endl; 8 9 return 0; 10 }
法二
但是肯定很多人都不知道有这个结论呀,那么我们可以用枚举来做。
由上可知这个最大不能组合数一定是不会超过ab的,当然比赛的时候我们不知道也可以猜,这个不能组合数一定不会特别大,而最好猜的就是ab。把ab内所有可能的解枚举出来,然后从后往前找不能被组合出来的数,那么第一个找到的数就是最大不能组合数。(顺便插一句,c++里的set是有序的,差点忘了。。。)
1 #include<iostream> 2 #include <set> 3 using namespace std; 4 5 int main(){ 6 set<int> s; 7 set<int>::iterator it; 8 int a,b; 9 cin>>a>>b; 10 for(int x = 0;a*x<=a*b;x++) //枚举a*b以内的所有解 11 for(int y = 0;a*x+b*y<=a*b;y++) 12 s.insert(a*x+b*y); 13 for(int i = a*b; i>=0; i--){ 14 if(s.find(i)==s.end()) { //i不在set中,那么i就是答案 15 cout<<i<<endl; 16 break; //找到后跳出循环 17 } 18 } 19 20 return 0; 21 }
法三
用动规做,其实也是枚举,如下是参考别人的代码,原文链接戳这里:
1 #include<iostream> 2 using namespace std; 3 4 int main() 5 { 6 int t=0,n,m; 7 cin>>n>>m; 8 int a[100005]; 9 a[0]=1; 10 for(int i=1;i<=n*m;i++){ 11 if(i>=n&&a[i-n]) 12 a[i]=1; 13 else if(i>=m&&a[i-m]) 14 a[i]=1; 15 } 16 for(int i=n*m;i>=0;i--) 17 { 18 if(!a[i]){ 19 cout<<i<<endl; 20 break; 21 } 22 } 23 24 return 0; 25 }
解释一下这段代码,能被标记成1的就相当于是能被组合出来的数,起始让a[0]为1,这样在循环的时候就可以先把n和m标记成1,这两个数也确实是可被m、n线性组合出来的(让另一个系数为0);如果一个数i被标记成1,那么i+n、i+m也可以被组合出来,所以也标记上1。循环的边界同样是m*n。
还看到一种,和这个差不多,用了清新脱俗的图表填充归纳法(瞎起的名字),可能更好理解,链接:这里这里
内容(以下为来自原文的引用):
对于4 7

4与7,大周期为7,小周期为4,当前层数能被填充的下一层对应的格子也能被填充。
开始位置为0 / 4,然后是4与7的周期差
在7*4后完成填充,最后填充的数字为7 * 4 – 4。
最大未被填充的数字在上一层,即 7*4 – 4 – 7。
替换字母后得到公式 a*b – a – b。
【代码 C++】

1 #include <cstdio> 2 #define mx 1000005 3 int data[mx]; 4 int main(){ 5 int i, j, a, b; 6 scanf("%d%d", &a, &b); 7 data[a] = data[b] = 1; 8 for (i = a + b / 2; i <= a*b; ++i){ 9 if (data[i - a]) ++data[i]; 10 if (data[i - b]) ++data[i]; 11 } 12 for (i = a*b; data[i]; --i); 13 printf("%d", i); 14 return 0; 15 }
另一个,思路和上面都一样,标准dp,令dp[i] = 1表示i能够由n和m组成,否则不能,则有dp[i] = dp[i-n]||dp[i-m] ? 1 : 0;
原文这里:

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <cmath> 5 using namespace std; 6 7 const int maxn = 1000005; 8 int dp[maxn]; 9 10 int main() { 11 int n, m; 12 while(scanf("%d %d", &n, &m) != EOF) { 13 memset(dp, 0, sizeof(dp)); 14 dp[n] = 1, dp[m] = 1; 15 int t = max(n, m); 16 for(int i = t + 1; i < maxn; i++) { 17 if(dp[i - n] || dp[i - m]) dp[i] = 1; 18 } 19 20 for(int i = maxn - 1; i >= 0; i--) { 21 if(!dp[i]) { 22 printf("%d\n", i); 23 break; 24 } 25 } 26 } 27 return 0; 28 }
