Linear Dependence and Span（线性相关和生成子空间）

其实这部分推导了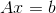 Ax=b 中b具有唯一解的条件。

从矩阵和向量相乘入手：

Ax=b ，其中是一个 $m\times n$ 的已知的矩阵，就是一个维的未知的列向量，得到的就是一个维的已知的列向量。等式左侧可以写为该形式：

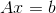
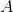
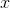
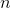
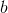
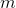
简化版就是：

相当于A视为一组(n个)列向量，每一个列向量与x中一个对应的元素(x有n个元素)相乘得到一个新的列向量，新的列向量相加得到结果b：一个m维列向量。这和线性组合的形式类似：

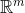
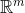
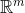
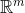
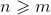
因此可以看作，A的列向量线性组合得到了b，b是m维的，可以视为是 $\mathbb{R}^{m}$ 空间中的一个点(m维度即m个坐标轴，b的m个分量/元素就是每一个坐标轴的坐标值)。一组向量的生成子空间 (span) 是原始向量线性组合后所能抵达的点的集合，这里可以视为 $\mathbb{R}^{m}$ 就是一个A的生成子空间。如果想让等式对任意b有解，也就是可以认为A中列向量的线性组合可以表示 $\mathbb{R}^{m}$ 空间(A的生成子空间)中任意一个元素，也就是任意一个m维列向量。这时候A其实包含了 $\mathbb{R}^{m}$ 中的基底，因此A至少要有m个列向量(基底的定义)，即 $n\geqslant m$ 。n可能大于m是因为A中的列向量不一定全部线性无关，可能存在冗余，因此是至少为m个，才能表示所有的b的情况，即等式对任意b都有解。

只能确保对任意b有解，不能保证唯一解。唯一解针对的情况其实就是A中列向量全部线性无关，没有冗余，即n=m，这时候矩阵A就成为了方阵(因为若是有冗余，比如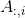 $A_{:,i}$ 和 $A_{:,j}$ 是线性相关的，比如是2倍的关系，那么 $x{_{i}}$ 和 $x{_{j}}$ 分别为1和1时得到的b是和 $x{_{i}}$ 和 $x{_{j}}$ 分别为3和0时得到的b是相同的，这就是同一个b对应的解x并不唯一)。

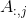
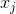
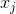
这就是有且只有一个解的充要条件：n=m，即A是方阵，且A中列向量线性无关。此时就可以利用A的逆矩阵通过公式

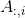
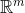
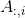
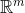
得到x。这时候再回顾上面矩阵运算的等式，可以这么理解：A中每一个列向量 $A_{:,i}$ 是 $\mathbb{R}^{m}$ 中的一个点，那么原点到这个点就能表示一个方向，这个列向量 $A_{:,i}$ 对应的 $x{_{i}}$ 可以视为这个方向上的步长或者距离，在 $\mathbb{R}^{m}$ 空间中从原点分别向每个方向上运动 $x{_{i}}$ 距离后就到达b这个点了。若是对二维空间，方向就可以理解为x轴和y轴。

注：一个列向量线性相关的方阵称为奇异的。

范数(Norms)

范数用来衡量向量的大小，将向量映射到非负的值，可以理解为向量到原点的距离，也可以理解为满足下列条件的任意一个函数：

1）f (x) = 0 ⇒ x = 0

2）f (x + y)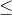 $\leq$ f(x) + f(y) (the triangle inequality)

3）∀α ∈ R, f(αx) = |α|f(x)

范数的形式为：

常用范数：

1. $\boldsymbol{L^{2}}$ 范数：

p=2，也称为欧几里得范数(Euclidean norm)，因为表示了到原点的欧几里得距离；

机器学习中常表示为||x||，对向量x可用 $x^{T}x$ 得到；

对每个元素的导数和向量中每个元素都有关(在分子上)。

2. 平方 $\boldsymbol{L^{2}}$ 范数：

相较 $\textup{}\mathbf{L^{2}}$ 范数而言计算更方便(没有开方)；

对每个元素的导数只和该元素有关；

在原点附近增长十分缓慢。

3. $\boldsymbol{L^{1}}$ 范数：

需要区分向量中零和非零元素的情况；

任意点的导数均相同；

任一元素向远离0的方向移动 $\varepsilon$ 距离， $L^{1}$ 范数增加 $\varepsilon$ 。

4. $\boldsymbol{L^{0}}$ 范数：

不符合范数的数学概念：元素变为a倍，范数不会变为a倍；

表示向量中非零元素的个数；

常用 $L^{1}$ 范数代替表示非零元素的个数。

5. $\boldsymbol{L^{\infty }}$ 范数(max norm)：

表示向量中具有最大幅度的元素的绝对值。

6. Frobenius norm：

衡量矩阵大小；

和向量的 $L^{2}$ 范数类似。

特殊类型的矩阵和向量

对角矩阵

长方形的矩阵也可能是对角阵；

对长方形对角矩阵D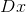，会涉及x中每个元素的放缩：若D是瘦长型，乘法结果会在末尾增添一些0；若D是宽胖型，会截掉末尾的元素。

正交

向量正交：

$x^{T}y=0$ ；

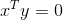
如果两个向量都有非零范数，则它们夹角为90度；

在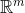 $\mathbb{R}^{m}$ 中，最多有m个范数非零向量正交；

若向量范数都为1，则称为标准正交；

正交矩阵：

行向量和列向量均标准正交的方阵，有：

正交矩阵求逆运算代价小。

矩阵分解

通过分解矩阵来发现矩阵表示成数组元素时不明显的函数性质。

特征分解：

特征分解是将矩阵分解成一组特征向量和特征值。矩阵A与一个向量相乘后若相当于对该向量做了缩放，这个向量就是矩阵A的特征向量，也就是矩阵A对它的特征向量有缩放作用，可用如下公式表示：

$A\nu =\lambda \nu$ ， $\lambda$ 是该特征向量对应的特征值，也就是缩放程度。

(补充理解：矩阵相当于一个线性变换，也就是对向量v做了线性变换后方向仍然不变，但是大小可能改变了。)

注：如果 $\nu$ 是A的特征向量，则缩放后的向量 $s\nu$ 也是A的特征向量，因此通常只考虑单位特征向量。

设矩阵A有n个线性无关的特征向量{ $v^{(1)},v^{(2)},...,v^{(n)}$ }，对应特征值{ $\lambda ^{(1)},\lambda ^{(2)},...,\lambda ^{(n)}$ }，将特征向量连接一个矩阵，使得每一列是一个特征向量： $V=[v^{(1)},v^{(2)},...,v^{(n)}]$ ，将特征值连成一个向量： $\mathbf{\lambda}=[\lambda ^{(1)},\lambda ^{(2)},...,\lambda ^{(n)}]^{T}$ ，此时矩阵A的特征分解可以表示为： $A=Vdiag(\lambda )V^{-1}$ 。这个形式的推导目前没有理清，不过应该和上文的该公式有关： $A\nu =\lambda \nu$ 。

注：不是每个矩阵都可以特征分解，有些分解还会涉及到复数，这里只讨论可以简单分解的矩阵，比如实对称矩阵，分解为该形式： $A=Q\Lambda Q^{T}$ ，Q是A的特征向量组成的正交矩阵(所以公式里是Q的转置矩阵，等价于逆矩阵)， $\Lambda$ 是对角矩阵，元素 $\Lambda_{i,i}$ 的特征值对应Q中的第i列的特征向量。由于Q是正交矩阵(所以每个特征向量都是互相正交的)，可以将A看作沿 $v^{(i)}$ 方向延展 $\lambda^{(i)}$ 倍的空间( $Q\Lambda$ 的结果就是Q中的每个列向量进行了 $\Lambda_{i,i}$ 倍的放缩也就是延展)，如下图所示。

实对称矩阵的特征分解也可以用于优化二次方程： $f(x)=x^{T}Ax$ ，其中限制 $\left \| x \right \|=1$ 。当x等于A的某个特征向量时，f将返回相应的特征值(可以从公式 $A=Q\Lambda Q^{T}$ 中推导得到，两边同时左乘Q的逆矩阵也就是转置矩阵，右乘Q)。在限制条件下，f的最大值是最大特征值，最小值是最小特征值。

所有特征值都是正数的矩阵被称为正定 (positive deﬁnite)；所有特征值都是非负数的矩阵被称为半正定 (positive semideﬁnite)。同样地，所有特征值都是负数的矩阵被称为负定 (negative deﬁnite)；所有特征值都是非正数的矩阵被称为半负定 (negative semideﬁnite)。半正定矩阵受到关注是因为它们保证 $\forall x,x^{T}Ax\geq 0$ (因为 $f(x)=x^{T}Ax$ 最小值是最小特征值，而半正定矩阵所有特征值都是非负数)。正定矩阵保证： $x^{T}Ax= 0 \Rightarrow x=0$ 。

奇异值分解(singular value decomposition, SVD)：

将矩阵分解为奇异向量(singular vector)和奇异值(singular value)。每个实数矩阵都有一个奇异值分解，不一定有特征分解。

奇异值分解将矩阵 A 分解成三个矩阵的乘积： $A=UD V^{T}$ ，若A是m*n的矩阵，则U是m*m，D是m*n，V是n*n。U和V是正交矩阵，D是对角矩阵，不一定是方阵，对角线上的元素为A的奇异值，U和V的列向量分别成为左奇异向量和右奇异向量。

我们可以用与 A 相关的特征分解去解释 A 的奇异值分解。A 的左奇异向量 (left singular vector) 是 $AA^{T}$ 的特征向量。A 的右奇异向量 (right singular vector) 是 $A^{T}A$ 的特征向量。A 的非零奇异值是 $A^{T}A$ 特征值的平方根，同时也是 $AA^{T}$ 特征值的平方根。

Moore-Penrose伪逆

求解问题： $Ax=y$ 。若是A的行数多于列数，该问题无解：相当于用低维的成分去求高维的信息，和前面线性相关部分的知识类似。若是A的行数小于列数，可能有多个解，可以使用伪逆来求解。矩阵A的伪逆定义为：

但实际运算为： $A^{+}=VD^{+}U^{T}$ ，矩阵 U，D 和 V 是矩阵 A奇异值分解后得到的矩阵。对角矩阵 D 的伪逆 $D^{+}$ 是其非零元素取倒数之后再转置得到的。

当矩阵 A 的行数少于列数时,使用伪逆求解线性方程是众多可能解法中的一种。具体地， $x=A^{+}y$ 是方程所有可行解中欧几里得范数 ∥x∥2 最小的一个。

当矩阵 A 的行数多于列数时，可能没有解。在这种情况下，通过伪逆得到的 x是使得 Ax 和 y 的欧几里得距离 ∥Ax − y∥2 最小的解。

迹运算

迹运算返回的是矩阵对角元素的和： $Tr(A)=\sum_{i}A_{i,i}$ 。

迹运算提供了另一种描述矩阵Frobenius 范数的方式： $\left \| A \right \|_{F}=\sqrt{Tr(AA^{T})}$ ；

迹运算在转置运算下不变， $Tr(A)=Tr(A^{T})$ ；

多个矩阵乘积的迹，和将这些矩阵中最后一个挪到最前面之后乘积的迹是相同的。当然，我们需要考虑挪动之后矩阵乘积依然定义良好： $Tr(ABC)=Tr(CAB)=Tr(BCA)$ 。或者更一般地：

标量在迹运算后仍然是它自己：a = Tr(a)。

行列式

行列式，记作 det(A)，是一个将方阵 A 映射到实数的函数。行列式等于矩阵特征值的乘积。行列式的绝对值可以用来衡量矩阵相乘后空间扩大或者缩小了多少。如果行列式是 0, 那么空间至少沿着某一维完全收缩了，使其失去了所有的体积。如果行列式是 1, 那么矩阵相乘没有改变空间体积。

主成分分析：

主成分分析可以看作一种有损压缩方法。编码方法可以是用低维表示，对于每个点 $x^{(i)}\epsilon \mathbb{R}^{n}$ ，编码为 $c^{(i)}\epsilon \mathbb{R}^{l}$ ，如果n>l，就相当于进行了压缩，减少了存储空间。找到一个编码函数，给定x可以得到c，即 $f(x)=c$ ，再找到一个解码函数， $x\approx g(f(x))$ 。为了简化解码器，可以使用矩阵乘法将编码映射回 $\mathbb{R}^{n}$ ， $g(c)=Dc$ ， $D\epsilon \mathbb{R}^{n\times l}$ 就是解码矩阵。

注：1. PCA限制 D 的列向量为彼此正交的（注意，除非 l = n，否则严格上 D 不是一个正交矩阵）；

2. 限制D中所有列向量有单位范数，否则如果按比例地缩小所有点对应的编码向量 ci，只需按比例放大 D:,i，即可保持结果不变，这就会有无穷多个解。

为了得到最优编码 $c^{*}$ ，可以通过最小化原始输入向量 x 和重构向量 $g(c^{*})$ 之间的距离，若使用 $L^{2}$ 范数来衡量距离可以得到：

可使用平方 $L^{2}$ 范数代替，因为两者是在相同的c值取到最小值，则可以得到：

$c^{*}=arg \underset{c}{min}\left \| x-g(c) \right \|_{2}^{2}$

$=arg \underset{c}{min}(x-g(c))^{T}(x-g(c))$

$=arg \underset{c}{min}(x^{T}x-x^{T}g(c)-g(c)^{T}x+g(c)^{T}g(c))$ ( $x^{T}g(c)$ 是标量，因此转置后不变，即 $x^{T}g(c)=g(c)^{T}x$ )

$=arg \underset{c}{min}(x^{T}x-2x^{T}g(c)+g(c)^{T}g(c))$ (因为 $x^{T}x$ 和变量无关，因此可以忽略)

$=arg \underset{c}{min}(-2x^{T}g(c)+g(c)^{T}g(c))$ (带入g(c)的定义)

$=arg \underset{c}{min}(-2x^{T}Dc+c^{T}D^{T}Dc)$

$=arg \underset{c}{min}(-2x^{T}Dc+c^{T}I_{l}c)$

$=arg \underset{c}{min}(-2x^{T}Dc+c^{T}c)$

接下来通过线性代数微积分求解： $\triangledown_{c} (-2x^{T}Dc+c^{T}c)=0$ ，得 $-2D^{T}x+2c=0$ ，得 $c=D^{T}x$ 。

可以看出，最优编码只需要进行一个矩阵乘法就可以： $f(x)=D^{T}x$ ，重构操作也可以定义为： $r(x)=g(f(x))=DD^{T}x$ 。

接下来就要选择D：我们是用同一个D对所有点进行解码，因此要最小化所有维度和所有点上的误差矩阵的Frobenius范数：

$D^{*}=arg \underset{D}{min}\sqrt{\sum_{i,j}(x_{j}^{(i)}-r(x^{(i)})_{j})^{2}}$ ，限制在 $DD^{T}=I_{l}$ 。（其中j是维度，i是点的个数）

想要求 $D^{*}$ ，可以先考虑l=1的情况，D就是一个向量d：

$d^{*}=arg \underset{d}{min}\sum_{i}\left \| x^{(i)}-dd^{T}x^{(i)} \right \|_{2}^{2}$ ，限制在 $\left \| d \right \|_{2}=1$ 。

$=arg \underset{d}{min}\sum_{i}\left \|x^{(i)}-d^{T}x^{(i)}d \right \|_{2}^{2}$

$=arg \underset{d}{min}\sum_{i}\left \|x^{(i)}-{x^{(i)}}^{T}dd \right \|_{2}^{2}$

接下来改写为矩阵形式( $X\epsilon \mathbb{R}^{m\times n}$ ，其中 $X_{i,:}={x^{(i)}}^{T}$ )：

$d^{*}=arg \underset{d}{min}\left \|X-Xdd^{T} \right \|_{F}^{2}$ ，限制在 $d^{T}d=1$ 。

$=arg \underset{d}{min}Tr({(X-Xdd^{T})}^{T}(X-Xdd^{T}))$

$=arg \underset{d}{min}Tr(X^{T}X-X^{T}Xdd^{T}-dd^{T}X^{T}X+dd^{T}X^{T}Xdd^{T})$

$=arg \underset{d}{min}Tr(X^{T}X)-Tr(X^{T}Xdd^{T})-Tr(dd^{T}X^{T}X)+Tr(dd^{T}X^{T}Xdd^{T})$ (删去与d无关的项)

$=arg \underset{d}{min}-Tr(X^{T}Xdd^{T})-Tr(dd^{T}X^{T}X)+Tr(dd^{T}X^{T}Xdd^{T})$ (循环改变迹运算中相乘矩阵的顺序不影响结果)

$=arg \underset{d}{min}-2Tr(X^{T}Xdd^{T})+Tr(X^{T}Xdd^{T}dd^{T})$ ，限制在 $d^{T}d=1$

$=arg \underset{d}{min}-2Tr(X^{T}Xdd^{T})+Tr(X^{T}Xdd^{T})$

$=arg \underset{d}{min}-Tr(X^{T}Xdd^{T})$

$=arg \underset{d}{max}Tr(X^{T}Xdd^{T})$

$=arg \underset{d}{max}Tr(d^{T}X^{T}Xd)$ ，可得最优的d是 $X^{T}X$ 最大特征值对应的特征向量。

以上是基于l=1的推导，事实上是得到了PCA中的第一个主成分，若要得到l个主成分，其实矩阵D就会由 $X^{T}X$ 的l个最大特征值对应的特征向量构成。

Deep Learning阅读笔记：Chapter 2—Linear Algebra

Linear Dependence and Span（线性相关和生成子空间）

范数(Norms)