协方差(Covariance)

协方差公式： $cov(X,Y)=E((X-E(X))(Y-E(Y)))$
协方差概念虽然早就学习过，不过自己是不能清楚讲明白的。借着这本书的学习，找了篇博客帮助理解，感觉写得很清晰：https://blog.csdn.net/GoodShot/article/details/79940438#commentBox
deep learning书中原文：协方差在某种意义上给出了两个变量线性相关性的强度以及这些变量的尺度。我们从以下两个方向理解协方差。

方法一：根据图片理解

三张图中横坐标均为变量X的取值，纵坐标为变量Y的取值，EX和EY分别表示变量X和Y的期望。
图一：可以看到X和Y的取值基本同时高于或低于它们的期望(图中(1)(3)的部分)： $(X-E(X))(Y-E(Y))> 0$ ，也就是X取值偏大的时候Y也偏大，X取值偏小则Y也偏小，即两者是正相关的关系。再仔细观察图中，(1)(3)的部分为主体，也存在(2)(4)的情况，但占比小，因此对 $(X-E(X))(Y-E(Y))$ 求期望可得到 $E((X-E(X))(Y-E(Y)))>0$ ，即协方差大于0。

图二：可以看到X和Y的取值基本是一个高于期望，而另一个低于期望(图中(2)(4)的部分)： $(X-E(X))(Y-E(Y))< 0$ ，也就是X取值偏大的时候Y偏小，X取值偏小时Y偏大，即两者是负相关的关系。图中(1)(3)所占比例较少，因此若是对式子 $(X-E(X))(Y-E(Y))$ 求期望，可得 $E((X-E(X))(Y-E(Y)))< 0$ ，即协方差小于0。

图三：变量X和Y无前面提到的两种线性相关关系，无论变量X如何取值，Y的取值都是均匀的， $(X-E(X))(Y-E(Y))$ 大于和小于0的情况均匀地分布在图中四个区域内，因此期望 $E((X-E(X))(Y-E(Y)))= 0$ ，表示两个变量间无线性相关，协方差为0。

如上三个图中，根据协方差 $E((X-E(X))(Y-E(Y)))$ 的符号可以判定变量X和Y之间的线性相关关系是正相关还是负相关，同时根据协方差 $E((X-E(X))(Y-E(Y)))$ 的大小还可以得到相关程度的强弱。这样就可以理解本文开头的内容：协方差在某种意义上给出了两个变量线性相关性的强度以及这些变量的尺度。

方法二：直接从公式入手

$cov(X,Y)=E((X-E(X))(Y-E(Y)))$

扫描二维码关注公众号，回复： 5346520 查看本文章

协方差的绝对值如果很大则意味着变量值变化很大并且它们同时距离各自的均值很远：协方差是一个期望，求期望的对象是变量X和Y偏离自己期望的程度(距离)。若是这个期望也就是协方差的绝对值大，则表明两个变量偏离自己的期望值很远，也就是变量值变化很大。如果协方差是正的，那么两个变量都倾向于同时取得相对较大的值。如果协方差是负的，那么其中一个变量倾向于取得相对较大的值的同时，另一个变量倾向于取得较小的值。

常见概率分布

Bernoulli分布(Bernoulli Distribution)：

单个二值型变量的分布，也就是变量只有两种取值：0和1，由单个参数 $\phi \in [0,1]$ 控制， $\phi$ 是变量取1的概率。

Multinoulli分布(Multinoulli Distribution)/范畴分布(Categorical Distribution)：

仍然是单个变量的分布，不过该变量的状态有k个，每一个状态取值为0或1，参数为一个向量 $p \in [0,1]^{k-1}$ ，每一个分量 $p^_{i}$ 表示取第i个状态的概率， $p^_{i}$ 等于0或1，最后一个状态的概率由 $1-1^{T}p$ 得到( $1^{T}$ 应该就是全为1的k-1维列向量， $1^{T}p$ 就是对 $p^_{i}$ 求和)，因此有限制： $1^{T}p\leq 1$ 。

Multinoulli分布可以用来表示对象分类的分布，因此其实不会把状态设置为数值1，也不会计算变量的期望和方差。

高斯分布(Gaussian Distribution)：

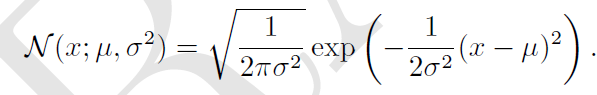
高斯分布是最常见的分布，概率密度通常写作如下形式，参数为期望 $\mu\in \mathbb{R}$ 和标准差 $\sigma\in \left ( 0 \right,\infty )$ ：

由于计算概率密度时 $\sigma$ 需要平方再倒数，计算复杂，因此用如下形式代替，令 $\beta =\frac{1}{\sigma^{2}}$ ， $\beta\in (0,\infty )$ ：

在实际应用中，当我们缺乏某个实数上的先验分布时，通常会假设为高斯分布，其合理性主要有两方面：

1. 我们想要建模的很多分布真实情况是比较接近正态分布的。中心极限定理 (central limit theorem) 说明很多独立随机变量的和近似服从正态分布。这意味着在实际中，很多复杂系统都可以被成功建模成正态分布的噪声，即使系统可以被分解成具有更多结构化行为的各个部分(把系统视为很多独立随机变量的叠加)。

2. 在具有相同方差的所有可能分布中，正态分布在实数上具有最大的不确定性，也就是说相当于我们加入的先验知识最少。

正态分布可以推广到 $\mathbb{R}^{n}$ 空间就是多维正态分布(multivariate normal distribution)，此时参数 $\mu$ 是一个向量，协方差是一个正定对称矩阵 $\sum$ ，概率密度函数如下：

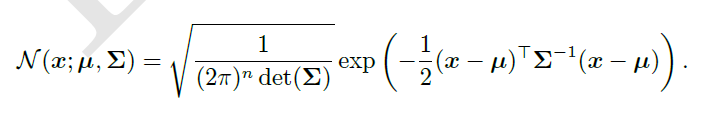
同样协方差矩阵计算复杂，因此有如下形式：

通常会把协方差矩阵固定为一个对角阵，对于各向同性高斯分布，其协方差矩阵是一个标量乘以单位矩阵。

指数分布(Exponential Distribution)：

其中 $1_{\geq 0}$ 是指数函数(Indicator function)，使得指数分布在x取负值时概率为0。深度学习中可能会经常用到这种在x=0处取得边界点(sharp point)的分布。

相近的有Laplace分布(Laplace distribution)，可以在任意一点 $\mu$ 处设置概率分布的峰值：

Dirac分布和经验分布：

首先介绍Dirac delta function $\delta \left ( x \right )$ ，表示只有在x=0处不为零，其积分为1，因此x=0处可以视为一个无穷大的值，其实就是信号与系统中的冲激函数。当我们想要让所有的概率都集中在一个点上时，可以利用该函数得到： $p(x) = \delta (x-\mu )$ 。Dirac delta function和一般的函数不同，并不是对每一个x值都有输出(仅对单个的特定点有输出)，它是一个广义函数(广义函数是通过积分定义的)。 $p(x) = \delta (x-\mu )$ 就可以被视为一系列函数的极限点，这些函数把除了 $\mu$ 以外的所有点的概率密度越变越小，而在 $x=\mu$ 处具有无穷大的概率密度函数(类似一个冲激信号)。Dirac delta function可以被用来构成经验分布(EDF，Empirical Distribution Functions)： $p(x)=\frac{1}{m}\sum_{i=1}^{m}\delta (x-x^{(i)})$ 。经验分布将概率密度 $\frac{1}{m}$ 分配给了点 $x^{(1)},x^{(2)},x^{(3)}...x^{(m)}$ 中的每一个(感觉有点像离散变量，但这些点x是给定数据集或者是采样点，也是被称为经验分布函数的原因)。

以另一种表示方式描述经验分布函数：x1,x2,⋯,xn 是总体 X 的一组容量为 n 的样本观测值，将它们按从小到大的顺序重新排列，那么对任意实数x，有

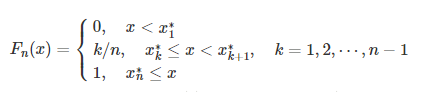，则称 Fn(x) 为总体 X 的经验分布函数，还可以简记为：

Fn(x)=1/n⋅ {x1,x2,⋯,xn}，其中 {x1,x2,⋯,xn} 表示 x1,x2,⋯,xn 中不大于 x 的个数。所以，求x的经验分布函数只需要根据已经有的样本点x1,x2,⋯,xn，找到其中比x小的点的个数k，除以观测次数(样本点个数)即可，所以Fn(x)就是n次独立重复实验中事件 $\left \{ X\leq x \right \}$ 出现的概率。这种根据已有样本点的大小分布和频数得到的分布函数，称为经验分布(和我们通常所指的分布函数意义相同，只不过这里借用了样本点数据来推断变量的概率分布，因为变量总体目前未知)。其应用在deep learning中就是：当我们在训练集上训练模型时，我们可以认为从这个训练集上得到的经验分布指明了我们采样来源的分布。

分布的混合(Mixtures of Distributions)

混合分布由多个组件构成，每个组件就是一个分布，每次采样要从中选择一个组件，这个选择取决于从一个Multinoulli分布中采样的结果(multinoulli中的多个状态就是不同的分布)：P(c)是对各组件的multinoulli分布。

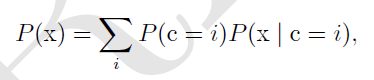
实值变量的经验分布对于每一个训练实例来说，就是以Dirac 分布为组件的混合分布(每个组件就来源于每个样本点)。混合模型是组合简单概率分布来生成更丰富的分布的一种简单策略。

最常见的混合模型就是高斯混合模型(Gaussian Mixture Model)，组件 $p(x|c=i)$ 就是高斯分布，每个组件有自己的参数 $\mu ^{(i)}$ 和 $\sum^{{}}^{(i)}$ 。也可以令协方差矩阵 $\sum^{{}}^{(i)}=\sum , \forall i$ 在组件间共享参数。除了均值和协方差，高斯混合模型的参数指明了给每个组件 i 的先验概率 (prior probability) $\alpha _{i}=P(c=i)$ 。‘‘先验’’ 一词表明了在观测到 x 之前传递给模型关于 c 的信念。作为对比，P (c | x) 是后验概率 (posterior probability)，因为它是在观测到 x 之后进行计算的。高斯混合模型是概率密度的通用逼近器 (universal approximator)，在这种意义上，任何平滑的概率密度都可以用具有足够多组件的高斯混合模型以任意精度来逼近。

上图就是一个高斯混合模型生成的例子：来自高斯混合模型的样本。在这个示例中，有三个组件。从左到右，第一个组件具有各向同性的协方差矩阵，这意味着它在每个方向上具有相同的方差。第二个组件具有对角的协方差矩阵，这意味着它可以沿着每个轴的对齐方向单独控制方差。该示例中，沿着 x2 轴的方差要比沿着x1 轴的方差大。第三个组件具有满秩的协方差矩阵，使它能够沿着任意基的方向单独地控制方差。

常用函数性质的应用

sigmoid：logistic sigmoid函数通常用来产生Bernoulli distribution的参数 $\phi$ ，因为其结果范围在(0，1)内。sigmoid函数公式如下：

$\sigma (x) = \frac{1}{1+exp(-x)}$ ，由于存在指数函数，因此在x绝对值较小的地方，函数变化较快，在x绝对值较大的地方会达到饱和状态，此时函数对输入微小的变化变得不敏感。

softplus：softplus函数可以用来产生正态分布的 β 和 σ 参数，因为它的范围是 (0, ∞)： $\zeta (x)=log(1+exp(x))$ 。

当处理包含 sigmoid 函数的表达式时它也经常出现。softplus 函数名来源于它是另外一个函数的平滑形式，这个函数是 $x^{+}=max(0,x)$ 。softplus函数图像如下：

logistic sigmoid function和softplus function的如下性质可能会在深度学习中用到：

信息论(Information Theory)

KL散度(Kullback-Leibler (KL) divergence)：用来衡量同一个变量X的两个单独的概率分布P(x)和Q(x)间的差异：

E就是求期望， $x\sim P$ 是指变量服从概率分布P。

我们可以先看一下香农熵的公式：，香农熵可以理解为从分布 P 中随机抽选一个事件，传达这条信息所需的最优平均信息长度。

再看一下交叉熵的公式：，交叉熵可理解为用分布 P 的最佳信息传递方式( $log(\frac{1}{p(x)})$ )来传达分布 Q 中随机抽选的一个事件 $Q(x)$ ，所需的平均信息长度。

而KL散度也可以写成如下形式：交叉熵与香农熵的差。

KL散度表示：用分布 P 的最佳信息传递方式来传达分布 Q，比用分布 Q 自己的最佳信息传递方式来传达分布 Q，平均多耗费的信息长度为 KL 散度，表达为 $D_{P}(Q)$ 或 $D_{KL}(Q||P)$ (注意两种写法中，P和P的顺序不同)，KL 散度衡量了两个分布之间的差异(所谓的分布P的最佳信息传递方式就是一种编码方式，这种编码能使服从概率分布P的变量产生的消息的平均编码长度最短，但我们现在用这种编码方式来编码服从分布Q的变量，此时变量Q产生的消息的平均编码长度要比使用最适合Q的编码方式的编码长度多多少)。

KL散度是非负的，可以理解，因为其他任一种编码方式一定劣于变量Q自己的最优编码方式。KL 散度为 0 当且仅当P 和 Q 在离散型变量的情况下是相同的分布，或者在连续型变量的情况下是 ‘‘几乎处处’’ 相同的。

因为KL 散度是非负的并且衡量的是两个分布之间的差异，它经常被用作分布之间的某种距离。然而，它并不是真的距离因为它不是对称的(距离是对称的，A与B之间的距离一定等于B与A之间的距离)：对于某些 P 和 Q， $D_{KL}(Q||P)\neq D_{KL}(P||Q)$ 。这种非对称性意味着选择 $D_{KL}(Q||P)$ 还是 $D_{KL}(P||Q)$ 影响很大。

当想让分布P和分布Q尽量贴近时，可选择两个衡量标准： $D_{KL}(Q||P)$ 和 $D_{KL}(P||Q)$ ：

1. 选择 $D_{KL}(P||Q)$ 时，要传达的信息来自分布P，传递方式来自分布Q， $D_{KL}(P||Q)=H_{Q}(P)-H(P)$ ，优化 $D_{KL}(P||Q)$ 相当于优化交叉熵 $H_{Q}(P)$ 和 $H(P)$ ，而后半部分与Q无关：因此要关注的是P中的常见事件，使其在Q决定的传递方式中也同样常见(因为常见事件的 $-log\frac{1}{p(x)}$ 会很大，传递成本高，若是在传递方式中和P本身不同，对两分布间的差异影响很大)。如下图所示，已有分布是P，让分布Q拟合时，这是利用 $D_{KL}(P||Q)$ 衡量得到的结果。关注的是P中常见事件(峰值部分)，因为存在两个相同峰值，Q拟合时为了保证两个峰值都能对应Q中的高概率部分，Q的峰值取在了两者中间，保证两个峰值的位置概率密度都不会过低。

2. 选择 $D_{KL}(Q||P)$ 时， $D_{KL}(Q||P)=H_{P}(Q)-H(Q)$ ，优化 $D_{KL}(Q||P)$ 时后半部分与P无关，要关注的是Q中的常见事件，因此要让Q的峰值能够对应到P中较高的位置(也可以理解为要让P中不常见的事件对应到Q中的不常见时间上：低谷与低谷对应)，由于P中两个峰值较远，分界线明显，Q选择了其中一个峰值，如下图所示(如果P中的两个峰值间没有足够强的低概率区域， $D_{KL}(Q||P)$ 可能也会模糊两个峰值取到中间部分)：

KL散度的不对称性参考了以下文章：

https://baijiahao.baidu.com/s?id=1593718515478182658&wfr=spider&for=pc

https://www.jianshu.com/p/43318a3dc715?from=timeline&isappinstalled=0

结构化概率模型(Structured Probabilistic Models)

机器学习算法会涉及到很多变量上的概率分布，这些分布涉及到的相互作用通常是介于很少变量之间的，因此使用单个函数来表示整个的联合分布是很低效的，反之我们可以将这个单个函数切分成许多因子的乘积形式，每个因子就只会涉及很少的变量。比如，假设我们有三个随机变量 a, b 和 c，并且 a 影响 b 的取值，b 影响 c 的取值，但是 a 和 c 在给定 b 时是条件独立的。我们可以把全部三个变量的概率分布重新表示为两个变量的概率分布的连乘形式： $p(a,b,c)=p(a)p(b|a)p(c|b)$ 。这种因子分解可以减少参数数量，降低联合分布表示的成本。当用图的结构来表示这种因子分解时，就称为结构化概率模型(Structured Probabilistic Models)或者图模型(graphical model)。

这里所说的图是指图论中的概念，由一些可以通过边互相连接的顶点的集合构成。有两种主要的结构化概率模型：有向的和无向的，这两种图模型都使用图 G，其中图的每个节点对应着一个随机变量，连接两个随机变量的边意味着概率分布可以表示成这两个随机变量之间的直接作用。

有向 (directed) 模型使用带有有向边的图，特别地，有向模型对于分布中的每一个随机变量 $x_{i}$ 都包含着一个影响因子，这个组成 $x_{i}$ 条件概率的影响因子被称为 $x_{i}$ 的双亲，记为 $P_{aG}(x_{i})$ ：

$p(x)=\prod_{i}p(x_{i}|P_{aG}(x_{i}))$ ，其实就是条件概率，双亲就是条件。

由上图可以看到，a和c是直接相互影响的，但a和e是要通过c间接相互影响的。

无向 (undirected) 模型的概念和有向模型完全不同，无向模型是带有无向边的图，它们将因子分解表示成一堆函数，这些函数通常不是任何类型的概率分布。G 中任何全部相连的节点构成的集合被称为团。无向模型中的每个团 $C^{(i)}$ 都伴随着一个因子 $\varphi ^{(i)}(C^{(i)})$ 。这些因子仅仅是函数，并不是概率分布。每个因子的输出都必须是非负的，但是并没有像概率分布中那样要求因子的和或者积分为 1。随机变量的联合概率和这些因子的乘积成比例：因子的值越大则可能性越大。因为乘积不能保证求和为1，因此进行归一化，归一化常数 Z 被定义为 $\varphi$ 函数乘积的所有状态的求和或积分：