希尔伯特变换简介

Hilbert变换简介

在数学与信号处理的领域中，一个实值函数 $x(t)$ ，其Hilbert变换记作 $\hat{x}(t)$ 定义为：
$\begin{array}{ll} \hat{x}(t)& =H[x(t)]\\ &=x(t)*\frac{1}{\pi t}\\ &=\frac{1}{\pi }\int^{\infty}_{-\infty}\frac{x(\tau)}{t-\tau}d\tau \end{array}$
在此H标示为希尔伯特变换。
希尔伯特反变换：
$\begin{array}{ll} x(t)&=H^{-1}[x(t)]\\ &=-\frac{1}{\pi }\int^{\infty}_{-\infty}\frac{\hat{x}(\tau)}{t-\tau}d\tau \end{array}$
因此，希尔伯特变换结果 $x'(t)$ 可以被解读为输入是 $x(t)$ 的线性时不变系统的输出，而此系统的脉冲响应为
$h(t)=\frac{1}{\pi t}$ 。
因此，Hilbert变换可以看成是将原始信号通过一个滤波器，或者一个转向器，这个系统的冲击响应为h(t)。
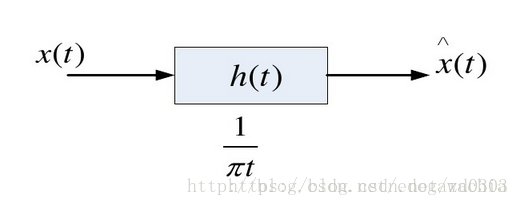
在这里插入图片描述
对 $h(t)$ 做傅里叶变换，得到
$H(\omega)=-jsgn(\omega)\\ =\lvert H(\omega)\rvert e^{j\phi(\omega)}$
或者写成
$H(\omega)= \left\{ \begin{array}{lcl} {-j} &\omega>0\\ 0&\omega=0\\ {+j} &\omega<0 \end{array} \right.$
其中 $sgn()$ 为符号函数。
$sgn(\omega)= \left\{ \begin{array}{ll} {1} &\omega>0\\ 0&\omega=0\\ {-1} &\omega<0 \end{array} \right.$
因此 $x(\omega)$ 的虚部 $\hat{x}(\omega)$ 的频率部分可以写成下式：
$\begin{array}{ll} \hat{X}(\omega)&=X(\omega)*H(\omega)\\ &=X(\omega)*(-jsgn(\omega))\\ &=-jX(\omega)*sgn(\omega)\\ \end{array}$
即：
$\hat{X}(\omega)= \left\{ \begin{array}{ll} -jX(\omega) &\omega>0\\ 0&\omega=0\\ jX(\omega) &\omega<0 \end{array} \right.$
也可以换成另一个写法（）
$\hat{X}(\omega)= \left\{ \begin{array}{ll} -j\frac{\omega}{|\omega|}X(\omega) &\omega\neq0\\ 0&\omega=0\\ \end{array} \right.$
因为 $X(t)$ 的频谱 $X(\omega)$ 的导数为
$X'(\omega)=j\omega X(\omega)$
所以一个信号的HIlbert变换可以理解为一个信号的平滑梯度（smoothed gradient）。平滑核函数为频域中的 $|\omega|^{-1}$ 。

在这里插入图片描述
从频谱上来看，这个滤波器将我们的原始信号的正频率部分乘以 $-j$ ，也就是说，保持幅度不变的条件下，将相位移动了 $-pi/2$ ，而对于负频率成分，移动了 $pi/2$ 。
下面这个示意图很直观地表示了Hilbert变换，在这里我画出了对原始信号做1到4次Hilbert变换的频谱示意图，是为了说明Hilbert变换的几个性质：
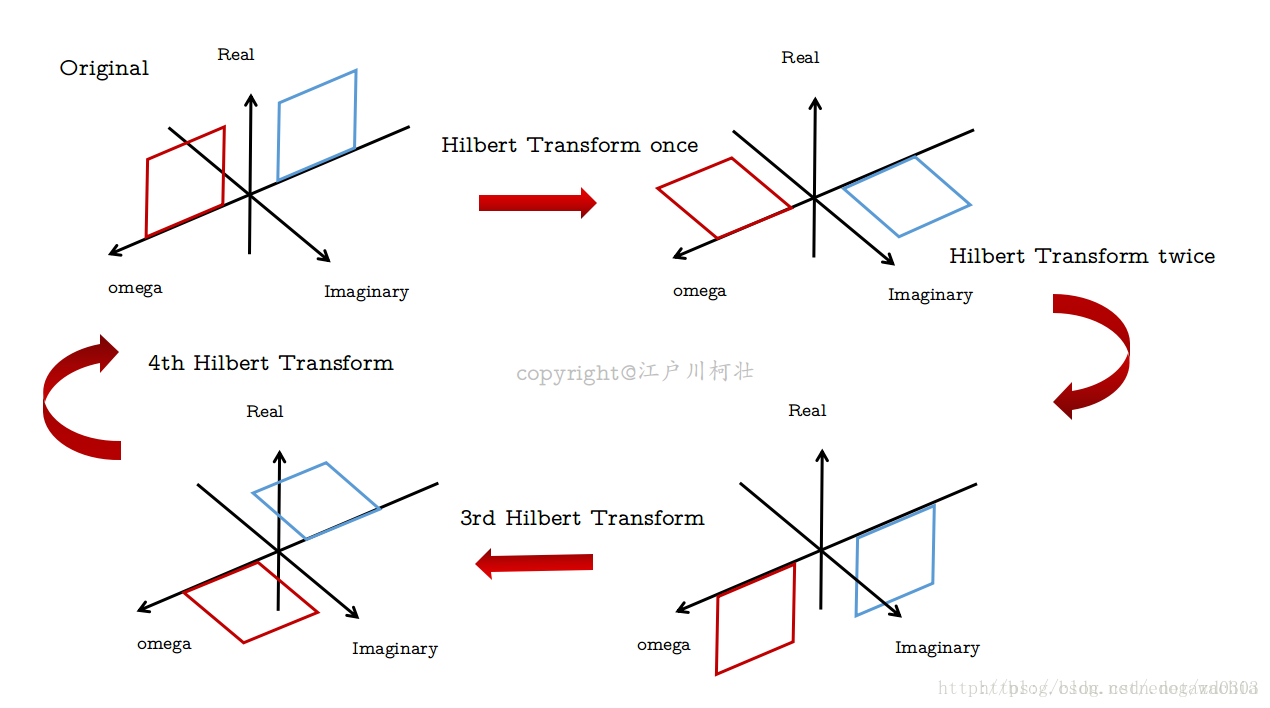
在这里插入图片描述

首先，可以看到，两次希尔伯特变换后，原信号相位翻转了180°，所以，Hilbert逆变换的公式显而易见，就是将正变换加一个符号即可。另外，还可以看到，Hilbert变换四次后就变回本身了。
Hilbert变换的性质有：

It is anti-symmetric: $H(-x)=-H(x)$
It suppresses the DC component: $H(0)=0$
Its energy is equal to one for all nonzero frequencies: $\begin{array}{ll} \lvert H(x)\rvert=1 & \forall x\ne0\end{array}$
$x(t)$ 的Hilbert变换信号 $\hat{x}(t)$ 与 $x(t)$ 正交： $\int_{\omega}\hat{x}(t)x(t)dt=0$

Hilbert变换物理意义

解析过程概念

一个实值函数 $x(t)$ ，其Hilbert变换记作 $\hat{x}(t)$ ，则 $x(t)$ 的解析信号为：
$\widetilde{x}=x(t)+j\hat{x}(t)$
这个过程有如下特点，首先，实部和虚部功率谱相同，自相关函数相同；另外，实部和虚部的互相关函数是一个奇函数。
其他的还有：
$R_{\hat{X}X}(\tau)=-\hat{R}_{X}(\tau)\\ R_{X\hat{X}}(\tau)=\hat{R}_{X}(\tau)\\ R_{X}(\tau)=2[R_{X}(\tau)+j\hat{R}_{X}(\tau)]$
解析信号的频谱只有正频段且幅度值为原来的两倍，实现了信号由双边谱转换成单边谱。
解析信号的功率谱也只有正频段，强度为原来的四倍。
$\widetilde{X}(\omega)=X(\omega)2u(\omega)=\\ \{ \begin{array}{lcl} {2X(\omega)} &\omega>0\\ {X(0)} &\omega=0\\ {0} &\omega<0 \end{array}$

欧拉公式（Euler‘s formula）的启发

$e^{ix} = cos(x)+isin(x)$
这个公式说明，用复指数信号可以表示成一个实数信号和一个虚数信号的和的形式。而且，这个实部和虚部是有关系的，一个是cos，一个是sin，两者相差pi/2，看sin和cos的傅里叶变换：

$cos(\omega_0t)$	$\pi[\delta(\omega+\omega_0)+\delta(\omega-\omega_0)]$
$sin(\omega_0t)$	$j\pi[\delta(\omega+\omega_0)-\delta(\omega-\omega_0)]$

可以看出，在正频率上和负频率上两者的相位上的先后顺序刚好相反，但是都是保持90°的差值。
看到这里，大概可以理解Hilbert变换的用意了吧。欧拉公式实际上是一种特殊的，或者说，最简单的Hilbert变换。
复指数信号，就是等号左边的那个，频谱就是一个脉冲，而且是 $2\pi\delta(\omega-\omega_0)$ 。只有正频率，且是两倍。虽然时域上是复数，但是在频域只有正分量，实际上是一种简化。

Hilbert解调原理

设窄带信号为 $x(t)=a(t)cos(2\pi f_st+\phi(t))$
其中 $f_s$ 是载波频率， $a(t)$ 是 $x(t)$ 的包络， $\phi(t)$ 是 $x(t)$ 的相位调制信号。
由于 $x(t)$ 是窄带信息，可设 $a(t)=[1+\sum^{M}_{m=1}x_mcos(2\pi f_mt+\gamma_m)]$ ， $f_m$ 为调幅信号 $a(t)$ 的频率分量， $\gamma_m$ 为 $f_m$ 的各初相角。因此 $a(t)$ 的各成分频率 $f_m<<f_s$ 。
对 $x(t)$ 进行Hilbert变换，并求解析信号，并使用欧拉公式表示：
$z(t)=x(t)+\hat{x}(t)=A(t)e^{j\Phi(t)}$
其中 $A(t)=a(t)=[1+\sum^{M}_{m=1}x_mcos(2\pi f_mt+\gamma_m)]$ ， $\Phi(t)=2\pi f_st+\phi(t)$ 。
容易发现
$a(t)=A(t)=\sqrt{x^2(t)+\hat{x}^2(t)}$
$\phi(t)=\Phi(t)-2\pi f_st=actan(\frac{x(t)}{\hat{x}(t)})-2\pi f_st$
并可以利用相位求解出解调频率： $f(t)=\frac{1}{2\pi}\frac{d\phi(t)}{dt}=\frac{1}{2\pi}\frac{d\Phi(t)}{dt}-f_s$

希尔伯特变换的意义

首先，将实数信号变换成解析信号的结果就是，把一个一维的信号变成了二维复平面上的信号，复数的模和幅角代表了信号的幅度和相位，如图所示
在这里插入图片描述
这样看来，似乎复数信号才是完整的，而实信号只是在复平面的实轴上的一个投影。我们知道，解析信号可以计算包络（瞬时振幅）和瞬时相位。在上图中可以看到，实际上我们计算的包络就是黑色的线围成的立体图形的边界在实部的投影，而计算这个边的投影也很简单，就是在复平面上的螺旋线中的每一个点的模值，也就是A(t) = sqrt(x^2(t) + Hilbert(x(t))^2)，而瞬时相位就是虚部（Hilbert变换后的）和实部（原始信号）在某一时间点的比值的arctan，瞬时频率就是它的导数。