现代通信原理5.1:信号的希尔伯特变换

1、希尔伯特变换式

  希尔伯特变换是以著名数学家大卫·希尔伯特(David Hilbert)来命名，是信号处理领域里一个重要变换。对于函数$g(t)$，其希尔伯特变换$\hat{g}(t)$定义为：
$$\begin{array}{rl}\hat{g}(t)& =\mathcal{H}[g(t)]\\ & =\frac{1}{\pi }{\int }_{-\infty }^{\infty }\frac{g(\tau )}{t-\tau }d\tau \\ & =g(t)\ast \frac{1}{\pi t}\end{array}\text{\hspace{1em}(1)}$$因此，希尔伯特变换结果$\hat{g}(t)$可以被看作将信号$g(t)$输入冲激响应为
$$h_Q(t)=\frac{1}{\pi t}\text{\hspace{1em}(2)}$$线性时不变系统得到的输出信号。
  进一步，我们可以得到希尔伯特逆变换为
$$\begin{array}{rl}g(t)& ={\mathcal{H}}^{-1}[\hat{g}(t)]\\ & =\frac{1}{\pi }{\int }_{-\infty }^{\infty }\frac{\hat{g}(\tau )}{t-\tau }d\tau \\ & =\hat{g}(t)\ast (-\frac{1}{\pi t})\end{array}\text{\hspace{1em}(3)}$$同样可以看成将$\hat{g}(t)$通过冲激响应为$-\frac{1}{\pi t}$的线性时不变系统。这样，我们可以用滤波器来分别实现希尔伯特变换及其逆变换，如图1中(a)、(b)所示。

图1 用滤波器实现希尔伯特变换与逆变换

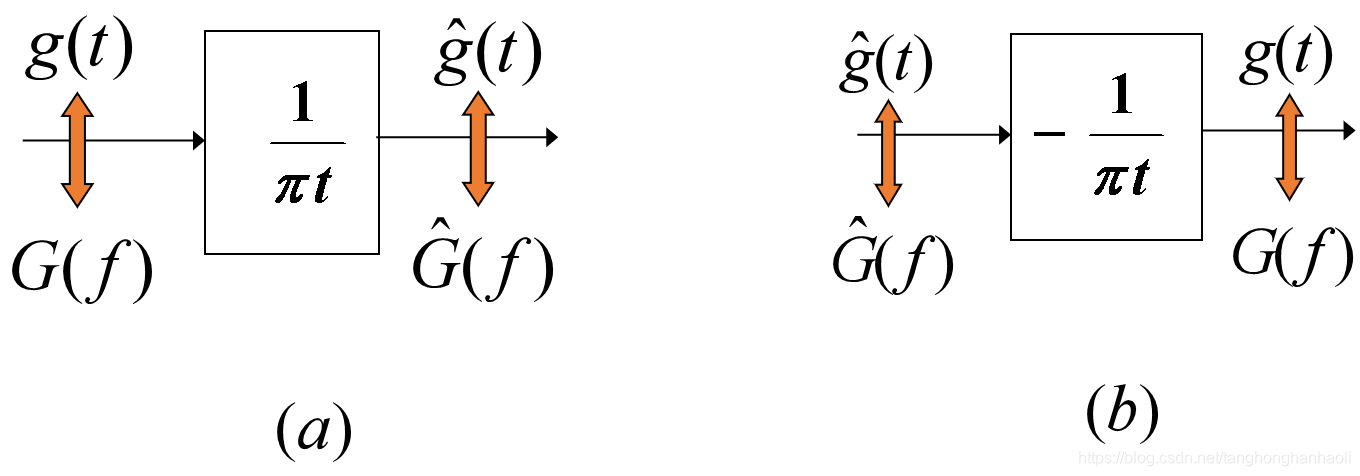
2、正交（希尔伯特）滤波器

  我们将$h_Q(t)=\frac{1}{\pi t}$称为正交滤波器，它的频率传递函数为
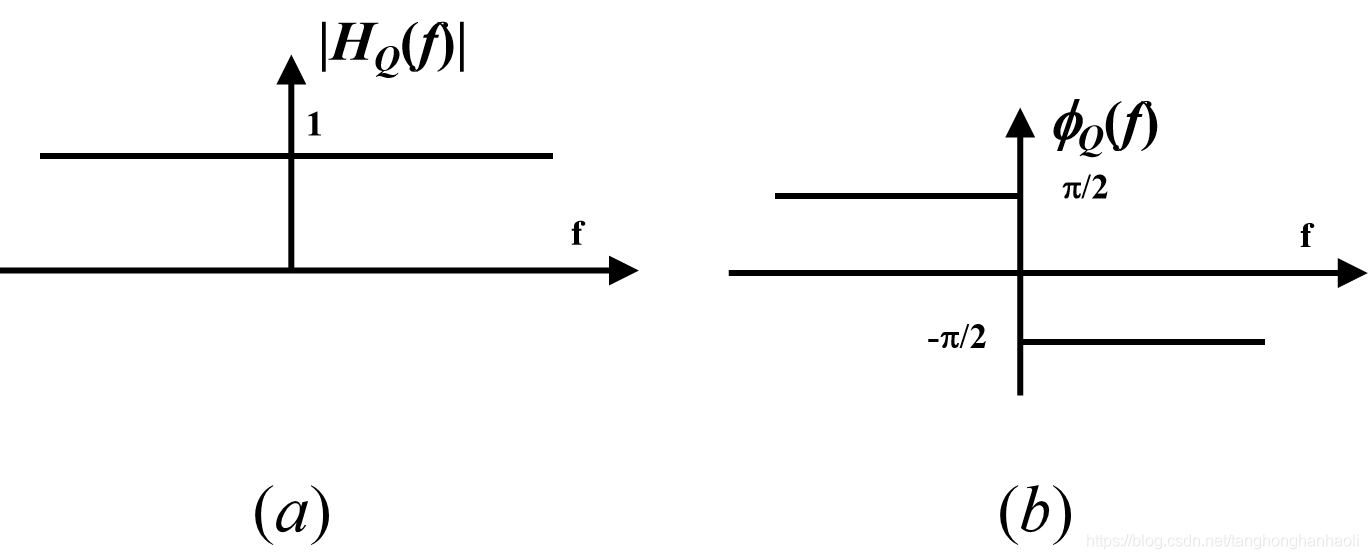
(4) H Q ( f ) = − j s g n ( f ) = { − j ,   f ≥ 0 + j ,   f &lt; 0 \tag{4} H_Q(f)=-j{\rm sgn}(f)=\{ \begin{aligned}-j,\ f\ge 0\\ +j,\ f&lt;0 \end{aligned} HQ​(f)=−jsgn(f)={ −j, f≥0+j, f<0​(4)这里$\mathrm{s}\mathrm{g}\mathrm{n}()$为符号函数。其幅频与相频特性分别如图2(a)、(b)所示。

图2

3、信号通过正交滤波器

  下面我们来看正交滤波器输入与输出信号关系。根据时域卷积定理，由于$\hat{g}(t)=g(t)\ast h_Q(t)$，我们有
$$\hat{G}(f)=G(f)H_Q(f)，\text{\hspace{1em}(5)}$$这里，$\hat{g}(t)\stackrel{\mathcal{H}.T.}{\leftrightarrow }\hat{G}(f)$，$g(t)\stackrel{\mathcal{H}.T.}{\leftrightarrow }G(f)$。因此，
$$\begin{array}{rl}\hat{G}(f)& =G(f)\cdot [-j\mathrm{s}\mathrm{g}\mathrm{n}(f)]\\ G(f)& =\hat{G}(f)\cdot [j\mathrm{s}\mathrm{g}\mathrm{n}(f)]\end{array}\text{\hspace{1em}(6)}$$从(6)我们可以得到
$$\begin{array}{rl}|\hat{G}(f)|& =|G(f)|\\ {\varphi }_{\hat{G}}(f)& ={\varphi }_G(f)-90^{\circ }\end{array}\text{\hspace{1em}(7)}$$显然，正交滤波器不改变信号幅值，仅相移$-90^{\circ }$。

【例1】 求余弦信号$g(t)=\cos 2\pi f_{c}t$的希尔伯特变换。
解：$g(t)$的希尔伯特变换的傅里叶变换为
$$\begin{array}{rl}\hat{G}(f)& =-j\mathrm{s}\mathrm{g}\mathrm{n}(f)G(f)\\ & =-j\mathrm{s}\mathrm{g}\mathrm{n}(f)\times \frac{1}{2}[\delta (f-f_c)+\delta (f+F_c)]\\ & =\frac{1}{j2}[\delta (f-f_c)-\delta (f+F_c)]\end{array}$$因此，$\hat{g}(t)=\sin 2\pi f_{c}t$。显然，余弦信号相移$-90^{\circ }$为正弦信号。
【例2】求信号$g(t)=\hat{m}(t)\sin 2\pi f_{c}t$的傅里叶变换。
解：
$$\begin{array}{rl}\hat{m}(t)\stackrel{\mathcal{F}.T.}{\leftrightarrow }& -j\mathrm{s}\mathrm{g}\mathrm{n}(f)M(f)\\ g(t)=\hat{m}(t)\sin 2\pi f_{c}t\stackrel{\mathcal{F}.T.}{\leftrightarrow }& G(f)=[-j\mathrm{s}\mathrm{g}\mathrm{n}(f)M(f)]\ast \frac{1}{j2}[\delta (f-f_c)+\delta (f+f_c)]\end{array}$$因此，有
$$G(f)=\frac{1}{2}[M(f+f_c)\mathrm{s}\mathrm{g}\mathrm{n}(f+f_c)-M(f-f_c)\mathrm{s}\mathrm{g}\mathrm{n}(f-f_c)].$$
【例3】求信号$g(t)=m(t)\cos 2\pi f_{c}t$的希尔伯特变换。
解：
$$\begin{array}{rl}g(t)& =m(t)\cos 2\pi f_{c}t\\ \hat{G}(f)& =-j\mathrm{s}\mathrm{g}\mathrm{n}(f)\times \frac{1}{2}[M(f-f_c)+M(f+f_c)]\\ & =\frac{1}{j2}[M(f-f_c)-M(f+f_c)]\\ \hat{g}(t)& =m(t)\sin 2\pi f_{c}t.\end{array}$$