很简单的例子:
已知有五个数,求前四个数与第五个数分 别相乘后的最大当数。给出两个算法分别如下:
max1(int a,b,c,d,e) max2(int a,b,c,d,e)
{ int x ; { int x
a=a*e; if (a>b)
b=b*e; x=a;
c=c*e; else
d=d*e; x=b;
if( a>b) if (c>x)
x=a; x=c;
else if (d>x)
x=b; x=d;
if (c>x) x=x*e;
x=c; print(x);
if (d>x) }
x=d;
print(x);
}

以上两个算法基于的数学模型是不同的,一个算法先积再求最大值,另一个算法先求最大值再求积,求从上表可以看出,后一个算法的效率明显要高于前一个算法。
数学建模就是把现实世界中的实际问题加以提炼,抽象为数学模型,求出模型的解,验证模型的合理性,并用该数学模型所提供的解答来解释现实问题,我们把数学知识的这一应用过程称为数学建模。
数学建模的基本方法
从分析问题的几种简单的、特殊的情况中,发现一般规律或作出某种猜想,从而找到解决问题的途径。这种研究问题方法叫做归纳法。即归纳法是从简单到复杂,由个别到一般的一种研究方法。
杨辉三角形的应用
【例】求n次二项式各项的系数:已知二项式的展 开式为:

问题分析:若只用的数学组合数学的知识,直接建模
 k=0,1,2,3……n。
k=0,1,2,3……n。
用这个公式去计算,n+1个系数,即使你考虑到了前后系数之间的数值关系:算法中也要有大量的乘法和除法运算,效率是很低的。
数学知识是各阶多项式的系数呈杨辉三角形的规律
(a+b)0 1
(a+b)1 1 1
(a+b)2 1 2 1
(a+b)3 1 3 3 1
(a+b)4 1 4 6 4 1
(a+b)5 ……
则求n次二项式的系数的数学模型就是求n阶杨辉三角形。
算法设计要点: 除了首尾两项系数为1外,当n>1时,(a+b)n的中间各项系数是(a+b)n-1的相应两项系数之和,如果把(a+b)n的n+1的系数列为数组c,则除了c(1)、c(n+1)恒为1外,设(a+b)n的系数为c(i),(a+b)n-1 的系数设为c’(i)。则有:
c(i)=c’(i)+c’(i-1)
而当n=1时,只有两个系数 c(1) 和 c(2) (值都为1)。不难看出,对任何n, (a+b)n的二项式系数可由(a+b)n-1的系数求得,直到n=1时,两个系数有确定值,故可写成递归子算法。
coeff(int a[ ],int n)
{ if (n==1)
{ a[1]=1;
a[2]=1;}
else
{ coeff(a,n-1);
a[n+1]=1;
for (i=n;i>=2;i- -)
a[i]=a[i]+a[i-1];
a[1]=1;
}
}
main( )
{int a[100],i,n;
input( n );
for(i=1;i<=n;i=i+1)
input(a[i]);
coeff(a,n);
for(i=1;i<=n;i=i+1)
print(a[i]);
}
最大公约数的应用
【例】数组中有n个数据,要将它们顺序循环向后移k位,即前面的元素向后移k位,后面的元素则循环向前移k位,例:1、2、3、4、5循环移3位后为:3、4、5、1、2。考虑到n会很大,不允许用2*n以上个空间来完成此题。
问题分析1:若题目中没有关于存储空间的限制,我们可以方便地开辟两个一维数组,一个存储原始数据,另一个存储移动后的数据。
main( )
{int a[100],b[100],i,n,k;
input(n,k );
for(i=0;i<n;i=i+1)
input(a[i]);
for(i=0;i<n;i=i+1)
b[(k+i) mod n]=a[i];
for(i=0;i<n;i=i+1)
print(b[i]);
}
这个算法的时间效率是n次移动(赋值)。
有可能k>n,这样移动会出现重复操作,可以在输入数据后,执行k = k mod n; 以保证不出现重复移动的问题。这个算法的移动(赋值)次数为k*n。当n较大时不是一个好的算法。
问题分析2:
● 将最后一个存储空间的数据,存储在临时存储空间中;
● 其余数据逐个向后移动一位。
这样操作共k次就能完成问题的要求。
算法2如下:
main( )
{int a[100],b[100],i,j,n,k,temp;
input(n,k);
for(i=0;i<n;i=i+1)
input(a[i]);
for(i=0;i<k;i=i+1)
{temp=a[n-1];
for(j=n-1;j>0;j=j-1)
a[j]=a[j-1];
a[0]= temp ;
}
for(i=0;i<n;i=i+1)
print(b[i]);
}
问题分析3 利用一个临时存储空间,把每一个数据一次移动到位:
1) 一组循环移动的情况:
通过计算我们可以确定某个元素移动后的具体位置,如n=5, k=3时:
0、1、2、3、4循环移3位后为2、3、4、0、1。
可通过计算得出0移到3的位置,3移到1的位置,1移到4的位置,4移到2的位置,2移到0的位置;一组移动(0-3-1-4-2-0)正好将全部数据按要求进行了移动。这样只需要一个辅助变量,每个数据只需一次移动就可完成整个移动过程。
如果算法就这样按一组移动去解决问题,就错了。因为还有其它情况。
2)多组循环移动的情况:算法不能按一组移动去解决问题。
看下一个例子,当n=6,k=3时,1、2、3、4、5、6经移动 的结果是4、5、6、1、2、3. 并不象上一个例子,一组循环 移动没有将全部数据移动到位。还需要(2-5-2)(3-6-3)两组移动,共要进行三组循环移动(1-4,2-5,3-6)才能将全部数据操作完毕。
循环移动的组数,与k、n的是怎么样的关系呢?
我们再看一个例子,当N=6,K=2时, 1、2、3、4、5、6经移动的结果是5、6、1、2、3、4. 1移到3的位置,3移到5的位置,5移到1的位置,一组移动完成了3个数据的移动,接下来,还有一组2-4-6-2。共进行二组循环移动,就能将全部数据移动完毕。
数学模型:循环移动的组数等于N与K的最大公约数。
算法设计:
1)编写函数,完成求n , k最大公约数m的功能
2)进行m组循环移动。
3)每组移动,和算法2一样,通过计算可以确定某个
元素移动后的具体位置。在移动之前,用临时变量
存储需要被覆盖的数据。
算法3如下:
main( )
{int a[100],b0,b1,i,j,n,k,m,tt;
print(“input the number of data”); input(n);
print(“input the distant of moving”); input(k );
for(i=0;i<n;i=i+1) input(a[i]);
m=ff(n,k);
for(j=0;j<m;j=j+1)
{b0= a[j]; tt=j;
for(i=0;i<n/m;i=i+1)
{tt=(tt+k) mod n;b1=a[tt]; a[tt]= b0; b0=b1;}
}
for(i=0;i<n;i=i+1)
print(a[i]);
}
ff ( int a ,int b)
{ t = 1;
for ( i = 2;i<=a and i<=b;i++)
while (a mod i=0 and b mod i=0 )
{ t=t * i ; a=a / i ; b= b / i ; }
return(t) ;
}
算法分析:每组循环移动都是从前向后进行的,一次移动需要两次赋值,总体大约需要赋值2n次。
能不能继续提高效率为赋值n次呢?请考虑改进每组循环移动的方式为从后开始移动,以提高运行效率。以例子说明:
n=6,k=2时,第一组循环移动0-2-4,在算法3中是这样实现的:
a[0]=>b0,
a[2]=>b1, b0(a[0])=>a[2],b1=> b0;
a[4]=>b1, b0(a[2])=> a[4],b1=> b0;
a[0]=>b1, b0(a[4])=> a[0] ,b1=> b0;
改进后(和算法2类似):
a[4]=>b ;a[2]=>a[4],a[0]=>a[2], b=>a[0]。
将每组最后一个数据元素存储在辅助存储空间,以后就可以安全地覆盖后面的数组元素了(注意覆盖顺序)。这样,一组循环移动只需一次将数据存入辅助存储空间,其后一次移动只需一次赋值,全部工作大约需要赋值n次就可完成。
公倍数的应用
【例】编程完成下面给“余”猜数的游戏:
你心里先想好一个1~100之间的整数x,将它分别除以3、5和7并得到三个余数。你把这三个余数告诉计算机,计算机能马上猜出你心中的这个数。游戏过程如下:
please think of a number between 1 and 100
your number divided by 3 has a remainder of? 1
your number divided by 5 has a remainder of? 0
your number divided by 7 has a remainder of? 5
let me think a moment…
your number was 40
问题分析:算法的关键是:找出余数与求解数之间的关系,
也就是建立问题的数学模型。
数学模型:
1)不难理解当s=u+3*v+3*w时,s除以3的余数与u除以3的
余数是一样的。
2)对s=cu+3*v+3*w,当c除以3余数为1的数时, s除以3的
余数与u除以3的余数也是一样的。证明如下:
c 除以 3余数为1,记c=3*k+1,则s=u+3*k*u+3*v+3*w,由1)的结论,上述结论正确。
记a,b,c分别为所猜数据d除以3,5,7后的余数,则
d=70*a+21*b+15*c。
为问题的数学模型,其中70称作a的系数,21称作b的系数,15称作c的系数。
由以上数学常识,a、b、c的系数必须满足:
1) b、c的系数能被3整除,且a的系数被3整除余1;这样d除以3的余数与a相同。
2) a、c的系数能被5整除,且b的系数被5整除余1;这样d除以5的余数与b相同。
3) a、b的系数能被7整除,且c的系数被7整除余1;这样d除以7的余数与c相同。
由此可见:
c的系数是3和5的最公倍数且被7整除余1,正好是15;
a的系数是7和5的最公倍数且被3整除余1,最小只能是70;
b的系数是7和3的最公倍数且被5整除余1,正好是21。
算法设计:用以上模型求解的数d,可能比100大,这时只要减去3,5,7的最小公倍数就是问题的解了。
main( )
{ int a,b,c,d;
print( “please think of a number between 1 and 100.”);
print( “your number divded by 3 has a remainker of”);
input(a);
print( “your number divded by 5 has a remainker of”);
input(b);
print( “your number divded by 7 has a remainker of”);
input(c);
print( “let me think a moment…”);
for (i=1 ,i<1500; i=i+1); //消耗时间,让做题者思考 d=70*a+21*b+15*c;
while (d>105) d=d-105;
print( “your number was ”, d);
}
裴波那契数列应用
【例】楼梯上有n阶台阶,上楼可以一步上1阶,也可以一步上2阶,编写算法计算共有多少种不同的上楼梯方法。
数学模型:此问题如果按照习惯,从前向后思考,也就是从第一阶开始,考虑怎么样走到第二阶、第三阶、第四阶……,则很难找出问题的规律;而反过来先思考“到第n阶有哪几种情况?”,答案就简单了,只有两种情况:
1) 从第n-1阶到第n阶;
2) 从第n-2阶到第n阶。
记n阶台阶的走法数为f(n),则
f(n)= 1 n=1
f(n)=2 n=2
f(n-1)+f(n-2) n>2
算法设计:算法可以用递归或循环完成。下面是问题的递归算法。
算法如下:
main( )
{ int n:;
print('n=');
input(n);
print('f(',n,')=',f(n));
}
f(int n)
{ if (n = 1 ) return(1);
if (n = 2 ) return(2);
else
return(f(x-1)+f(x-2));
}
递推关系求解方程
【例】核反应堆中有α和β两种粒子,每秒钟内一个α粒子可以反应产生3个β粒子,而一个β粒子可以反应产生1个α粒子和2个β粒子。若在t=0时刻的反应堆中只有一个α粒子,求在t时刻的反应堆中α粒子和β粒子数。
数学模型1:本题中共涉及两个变量,设在i时刻α粒子数为ni,β粒子数为mi,则有:n0=1,m0=0,ni=mi—1,mi=3ni—1+2mi—1
算法设计1:本题方便转化为求数列N和M的第t项,可用递推的方法求得nt和mt,此模型的算法如下:
main()
{ int n[100],m[100],t,i;
input(t);
n[0]=1; //初始化操作
m[0]=0;
for (i=1;i<=t;i++) //进行t次递推
{ n[i]=m[i-1];
m[i]=3 * n[i-1] + 2 * m[i-1]; }
print(n[t]); //输出结果
print(m[t]);
}
算法分析1:此模型的空间需求较小,时间复杂度为O(n),但随着n的增大,所需时间越来越大。
数学模型2:设在t时刻的α粒子数为f(t),β粒子数为g(t),依题可知:
g(t)=3f(t -1)+2g(t -1) (1)
f(t)=g(t -1) (2)
g(0)=0,f(0)=1
下面求解这个递归函数的非递归形式
由(2)得f(t -1)=g(t-2) (3)
将(3)代入(1)得
g(t)=3g(t -2)+2g(t-1) (t≥2) (4)
g(0)=0,g(1)=3
(4)式的特征根方程为:
x2—2x—3=0
其特征根为x1=3,x2= -1
所以该式的递推关系的通解为
g(t)=C1·3t+C2·( -1)t
代入初值g(0)=0,g(1)=3得
C1+C2=0
3C1—C2=3
解此方程组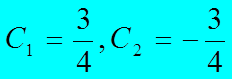
所以该递推关系的解为
∴g(t)=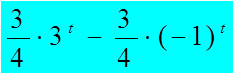
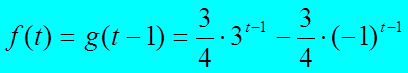
即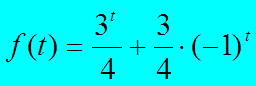
由数学模型2,设计算法2如下
main()
{ int t,i;
input(t);
n=int(exp(t*ln(3)));
m=int(exp((t+1)*ln(3)));
if (t mod 2=1)
{ n=n-3; m=m+3;}
else
{ n=n+3; m=m-3;}
n=int(n/4); // 4|n
m=int(m/4); // 4|m
print(n);
print(m);
}
算法分析:在数学模型2中,运用数学的方法建立了递归函数并转化为非递归函数。它的优点是算法的复杂性与问题的规模无关。针对某一具体数据,问题的规模对时间的影响微乎其微。