0 前言
本文参考
- 《控制系统仿真与计算机辅助设计 · 第2版》薛定宇 机械工业出版社
- 《MATLAB for Control Engineers》Katsuhiko Ogata
- 现代控制理论线性系统入门(一)状态方程描述下的动态系统
- 《现代控制理论基础》— 2 什么是状态与状态空间
本文已假设读者具有自动控制原理的理论基础
本教程笔记基于 MATLAB R2020a
1 线性系统的传递函数模型
在经典控制之中,连续线性系统一般可以用传递函数表示。还可以使用零极点来表示
我们知道传递函数的定义式为:
G ( s ) = C ( s ) R ( s ) = b 0 s m + b 1 s m − 1 + ⋅ ⋅ ⋅ + b m − 1 s + b m a 0 s n + a 1 s n − 1 + ⋅ ⋅ ⋅ + a n − 1 s + a n = M ( s ) N ( s ) G(s)={\frac{C(s)}{R(s)}}={\frac{b_0s^m+b_1s^{m-1}+···+b_{m-1}s+b_m}{a_0s^n+a_1s^{n-1}+···+a_{n-1}s+a_n}}={\frac{M(s)}{N(s)}} G(s)=R(s)C(s)=a0sn+a1sn−1+⋅⋅⋅+an−1s+anb0sm+b1sm−1+⋅⋅⋅+bm−1s+bm=N(s)M(s)
对分母包含高次多项式的传递函数,进行部分分式展开的计算是很费时间的。在这种情况下, 建议采用 MATLAB 来完成。 MATLAB 有一条命令能够获得 C ( s ) / R ( s ) C(s)/R(s) C(s)/R(s) 的部分分式展开式。它还有一条命令能够获得 C ( s ) / R ( s ) C(s)/R(s) C(s)/R(s) 的零点和极点。
G ( s ) = C ( s ) R ( s ) = n u m d e n = b 0 s m + b 1 s m − 1 + ⋅ ⋅ ⋅ + b m s + b m + 1 s n + a 1 s n − 1 + ⋅ ⋅ ⋅ + a n − 1 s + a n G(s)={\frac{C(s)}{R(s)}}={\frac{num}{den}}={\frac{b_0s^m+b_1s^{m-1}+···+b_{m}s+b_{m+1}}{s^n+a_1s^{n-1}+···+a_{n-1}s+a_n}} G(s)=R(s)C(s)=dennum=sn+a1sn−1+⋅⋅⋅+an−1s+anb0sm+b1sm−1+⋅⋅⋅+bms+bm+1
其中某些 a i a_i ai 和 b i b_i bi 可以是零。对于物理可实现系统来说,一定要满足 m ≤ n m ≤ n m≤n ,这种情况下又称为系统为正则(proper),若 m < n m < n m<n ,则称系统为严格正则。 n − m n-m n−m 又称为系统的相对阶次。
在 MATLAB中,行向量 num 和 den 具体指明了传递函数的分子和分母的系数。也就是说:
n u m = [ b 0 b 1 . . . b n ] d e n = [ 1 a 1 . . . a n ] num=[b_0 \quad b_1 \quad ... \quad b_n]\\den=[1 \quad a_1 \quad ... \quad a_n] num=[b0b1...bn]den=[1a1...an]
1.1 用一个对象表示传递函数模型 tf():
e g . G ( s ) = s 3 + 7 s 2 + 24 s + 24 s 4 + 10 s 3 + 35 s 2 + 50 s + 24 eg.\quad G(s)={\frac{s^3+7s^2+24s+24}{s^4+10s^3+35s^2+50s+24}} eg.G(s)=s4+10s3+35s2+50s+24s3+7s2+24s+24
则代码如下:
num = [1 7 24 24];
den = [1 10 35 50 24]; % 按 s 降幂顺序输入多项式系数
G = tf(num, den);
或者有第二种方式:
s = tf('s'); % 定义传递函数的算子
G = (s^3+7*s^2+24*s+24)/(s^4+10*s^3+35*s^2+50*s+24);
这个时候我们就能得到系统的数学模型 G G G 了

关于tf函数详细描述可看右边链接:https://www.mathworks.com/help/control/ref/tf.html
1.2 不是完全展开形式使用 conv():
如果分子或分母多项式给出的不是完全展开的形式,而是若干个因式的乘积,则事先需要将其变换为完全展开的形式,两个多项式的乘积在MATLAB 下可以借用卷积求取函数 conv() 求出:
p = conv(p1, p2); % p2 与 p2 是两个多项式,这个函数返回乘积多项式 p
如果有 3 个多项式的乘积,就需要嵌套适用此函数:
p = conv(p1, conv(p2, p3));
G ( s ) = 5 ( s + 2.4 ) ( s + 1 ) 2 ( s 2 + 3 s + 4 ) ( s 2 + 1 ) G(s)={\frac {5(s+2.4)}{(s+1)^2(s^2+3s+4)(s^2+1)}} G(s)=(s+1)2(s2+3s+4)(s2+1)5(s+2.4)
则上式我们可以采用:
num = 5*[1, 2.4];
den = conv([1, 1], conv([1, 1], conv([1 3 4], [1 0 1])));
G = tf(num, den)
则输出结果:

也可以采用算子直观输入:
s = tf('s');
G = 5*(s+2.4)/((s+1)^2*(s^2+3*s+4)*(s^2+1));
用算子输入通常比较方便,但是不适合自动类型的程序。
1.3 使用 stepplot() 与 impulseplot() 画出系统的阶跃响应与冲激响应图像
代码如下:
stepplot(G);
% impulseplot(G); % 不展示结果
则我们可以看到这个系统的阶跃响应输出曲线:
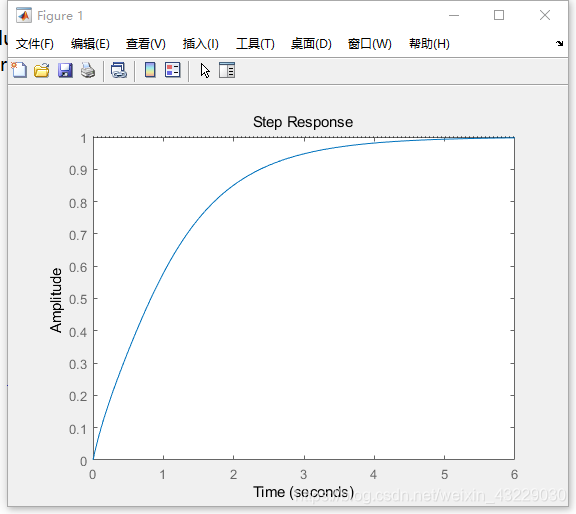
1.4 使用 step() 与 impulse() 绘制系统的阶跃响应和冲激响应
与 1.3 同理,也可以不转换成系统直接画出响应,如下:
num = [0 0 10];
den = [1 2 10];
step(num, den)
1.5 使用 get() 获取对象 tf 属性
代码如下:
get(G);
则我们可以得到如下信息:
Numerator: {[0 0 0 0 0 5 12]}
Denominator: {[1 5 12 16 15 11 4]}
Variable: ‘s’
IODelay: 0
InputDelay: 0
OutputDelay: 0
Ts: 0
TimeUnit: ‘seconds’
InputName: {’’}
InputUnit: {’’}
InputGroup: [1×1 struct]
OutputName: {’’}
OutputUnit: {’’}
OutputGroup: [1×1 struct]
Notes: [0×1 string]
UserData: []
Name: ‘’
SamplingGrid: [1×1 struct]
我们可以直接修改系统的延迟时间常数:
G.IODelay = 2.1;
1.6 使用 tfdata() 来提取系统的分子分母多项式
代码如下:
[n, d] = tfdata(G, 'v'); % 'v' 表示想获得数值
或者:
num = G.num{1}; % 直接提取分子多项式
den = G.den{1}; % 直接提取分母多项式
% 这里的{1}实际上为{1, 1},表示第一路输入和第一路输出之间的传递函数,该方法直接适合MIMO系统的描述
1.7 使用 residue() 求部分分式展开式中的留数,极点和直接项
则我们直接进入代码:
num = [b0 b1 ... bn];
den = [a0 a1 ... an];
[r, p, k] = residue(num, den);
可以求出两个多项式 C ( s ) C( s ) C(s) 和 R ( s ) R ( s ) R(s) 之比的部分分式展开式中的留数 ( r ) ( r ) (r) ,极点 ( p ) (p) (p) 和直接项 ( k ) (k) (k) 。
e . g . B ( s ) / A ( s ) = 2 s 3 + 5 s 2 + 3 s + 6 s 3 + 6 s 2 + 11 s + 6 e.g. \quad B(s)/A(s) = {\frac{2s^3+5s^2+3s+6}{s^3+6s^2+11s+6}} e.g.B(s)/A(s)=s3+6s2+11s+62s3+5s2+3s+6
num = [2 5 3 6];
den = [1 6 11 6];
[r, p, k] = residue(num, den)
则输出如下:
r =
-6.0000
-4.0000
3.0000p =
-3.0000
-2.0000
-1.0000k =
2
可以看出,留数由向量 r 给出,极点位置由向量 p 给 出, 直接项则由向量 k 给 出。上述结果就是 B ( s ) / A ( s ) B ( s ) /A( s ) B(s)/A(s) 的部分分式展开式 :
B ( s ) / A ( s ) = 2 s 3 + 5 s 2 + 3 s + 6 s 3 + 6 s 2 + 11 s + 6 = − 6 s + 3 + − 4 s + 2 + 3 s + 1 + 2 B(s)/A(s) = {\frac{2s^3+5s^2+3s+6}{s^3+6s^2+11s+6}} ={\frac{-6}{s+3}}+{\frac{-4}{s+2}+{\frac{3}{s+1}+2}} B(s)/A(s)=s3+6s2+11s+62s3+5s2+3s+6=s+3−6+s+2−4+s+13+2
还可以反过来部分分式展开式构成(分子和分母)多项式。
r = [-6 -4 3];
p = [-3 -2 -1];
k = 2;
[num, den] = residue(r, p, k)
则输出如下:
num =
2 5 3 6
den =
1 6 11 6
1.8 使用 damp(num, den) 求出计算系统的闭环根、阻尼比、无阻尼振荡频率
num = [0 0 10];
den = [1 2 10];
G = tf(num, den);
damp(den);
得出结果如下:
Pole Damping Frequency Time Constant (rad/TimeUnit) (TimeUnit)-1.00e+00 + 3.00e+00i 3.16e-01 3.16e+00 1.00e+00
-1.00e+00 - 3.00e+00i 3.16e-01 3.16e+00 1.00e+00
所以:
闭环根为:s1 = -1+3j,s2 = -1-3j
阻尼比:ζ=0.316
无阻尼振荡频率:ωn=3.16
1.9 使用 printsys() 从留数,极点和直接项获得原始函数
代码如下:
printsys(num, den, 's')
输出结果如下:
num/den =
2 s^3 + 5 s^2 + 3 s + 6
---------------------------
s^3 + 6 s^2 + 11 s + 6
1.10 使用 [num, den]=ord2( ω n , ζ \omega_n,\zeta ωn,ζ) 建立二阶系统标准模型
[num, den]= ord2(1, 1);
printsys(num, den, 's')
得到输出结果如下:
num/den =
1
-------------
s^2 + 2 s + 1
2 线性系统的状态方程模型
注:笔者目前暂未学习现代控制理论,所以此处参考了来自知乎的:现代控制理论线性系统入门(一)状态方程描述下的动态系统 以及 《现代控制理论基础》— 2 什么是状态与状态空间
-
状态方程是描述控制系统的另一种重要的方式。和传递函数不同,状态方程可以描述更广的一类系统模型,包括非线性模型。
-
现代控制理论有一种不错的方法,能够很快判断系统稳定性也很便于设计控制器。它就是基于状态空间描述的状态方程模型,由于状态方程模型基于矩阵,更便于现代的计算机求解。
-
把一个系统当作黑箱,那么这个黑箱和外界的交互关系,就对应了有不同时间的输入输出。在 t t t 时刻,这 m m m 个会影响系统的输入量在控制理论里称为 控制变量 ,而这 p p p 个系统输出的可以被传感器测量的量称为 测量变量 ,现在我们做一些基本假设,限制一些条件,只研究连续时变的线性系统。而且系统的行为,即输出量,由描述系统的函数通过输入量,在时域上唯一确定。我们把系统的行为分为 静态和动态 两类。系统的状态受过去影响,随时间变化。这样的系统被称为动态系统。
-
状态方程: 有 n n n 个状态 x 1 , x 2 , ⋅ ⋅ ⋅ , x n x_1,x_2,···,x_n x1,x2,⋅⋅⋅,xn ,构成状态变量向量,当且仅当 p p p 个输出信号 y 1 , y 2 , ⋅ ⋅ ⋅ , y p y_1,y_2,···,y_p y1,y2,⋅⋅⋅,yp 完全由初始状态 x 1 ( t 0 ) , x 2 ( t 0 ) , x 3 ( t 0 ) , ⋅ ⋅ ⋅ , x n ( t 0 ) x_1(t_0),x_2(t_0),x_3(t_0),···,x_n(t_0) x1(t0),x2(t0),x3(t0),⋅⋅⋅,xn(t0) 以及 m m m 个输入量 u 1 ( τ ) , u 2 ( τ ) , ⋅ ⋅ ⋅ , u m ( τ ) u_1(\tau),u_2(\tau),···,u_m(\tau) u1(τ),u2(τ),⋅⋅⋅,um(τ) 在 τ ∈ [ t 0 , t ] \tau ∈ [t_0,t] τ∈[t0,t] 内的历史决定,则此动态系统的状态方程可以可以由有限个一阶常微分方程组描述:
x 1 ⋅ = f 1 ( x 1 , x 2 , ⋅ ⋅ ⋅ , x n , u 1 , u 2 , ⋅ ⋅ ⋅ , u m ) , x 1 ( t 0 ) = x 1 , 0 x 2 ⋅ = f 1 ( x 1 , x 2 , ⋅ ⋅ ⋅ , x n , u 1 , u 2 , ⋅ ⋅ ⋅ , u m ) , x 2 ( t 0 ) = x 2 , 0 ⋅ ⋅ ⋅ ⋅ x n ⋅ = f 1 ( x 1 , x 2 , ⋅ ⋅ ⋅ , x n , u 1 , u 2 , ⋅ ⋅ ⋅ , u m ) , x n ( t 0 ) = x n , 0 \mathop{x_1}\limits^{·}=f_1(x_1,x_2,···,x_n,u_1,u_2,···,u_m),x_1(t_0)=x_{1,0}\\ \mathop{x_2}\limits^{·}=f_1(x_1,x_2,···,x_n,u_1,u_2,···,u_m),x_2(t_0)=x_{2,0}\\ ····\\ \mathop{x_n}\limits^{·}=f_1(x_1,x_2,···,x_n,u_1,u_2,···,u_m),x_n(t_0)=x_{n,0}\\ x1⋅=f1(x1,x2,⋅⋅⋅,xn,u1,u2,⋅⋅⋅,um),x1(t0)=x1,0x2⋅=f1(x1,x2,⋅⋅⋅,xn,u1,u2,⋅⋅⋅,um),x2(t0)=x2,0⋅⋅⋅⋅xn⋅=f1(x1,x2,⋅⋅⋅,xn,u1,u2,⋅⋅⋅,um),xn(t0)=xn,0
同时输出方程为:
y 1 = h 1 ( x 1 , x 2 , ⋅ ⋅ ⋅ , x n , u 1 , u 2 , ⋅ ⋅ ⋅ , u m , t ) y 2 = h 2 ( x 1 , x 2 , ⋅ ⋅ ⋅ , x n , u 1 , u 2 , ⋅ ⋅ ⋅ , u m , t ) ⋅ ⋅ ⋅ ⋅ y p = h p ( x 1 , x 2 , ⋅ ⋅ ⋅ , x n , u 1 , u 2 , ⋅ ⋅ ⋅ , u m , t ) y_1=h_1(x_1,x_2,···,x_n,u_1,u_2,···,u_m,t)\\ y_2=h_2(x_1,x_2,···,x_n,u_1,u_2,···,u_m,t)\\ ····\\ y_p=h_p(x_1,x_2,···,x_n,u_1,u_2,···,u_m,t)\\ y1=h1(x1,x2,⋅⋅⋅,xn,u1,u2,⋅⋅⋅,um,t)y2=h2(x1,x2,⋅⋅⋅,xn,u1,u2,⋅⋅⋅,um,t)⋅⋅⋅⋅yp=hp(x1,x2,⋅⋅⋅,xn,u1,u2,⋅⋅⋅,um,t)
当然我们可以向量形式来描述这些方程组:
x = [ x 1 , x 2 , ⋅ ⋅ ⋅ , x n ] T u = [ u 1 , u 2 , ⋅ ⋅ ⋅ , u m ] T y = [ y 1 , y 2 , ⋅ ⋅ ⋅ , y p ] T \textbf{x}=[x_1,x_2,···,x_n]^T \\ \textbf{u}=[u_1,u_2,···,u_m]^T \\ \textbf{y}=[y_1,y_2,···,y_p]^T x=[x1,x2,⋅⋅⋅,xn]Tu=[u1,u2,⋅⋅⋅,um]Ty=[y1,y2,⋅⋅⋅,yp]T
我们就可以用更加紧凑的方式来描述它:
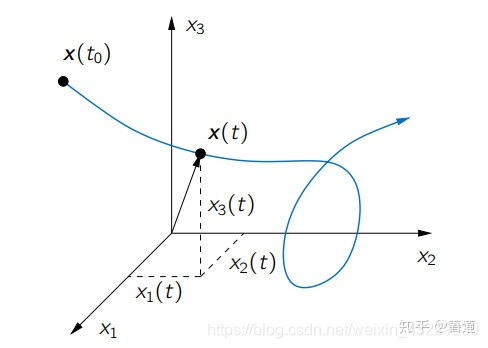
{ x ⋅ = f ( x , u , t ) y = h ( x , u , t ) x ( t 0 ) = x 0 \left\{ \begin{aligned} \mathop{\textbf{x}}\limits^{·}=f(\textbf{x},\textbf{u},t) \\ \textbf{y}=h(\textbf{x},\textbf{u},t)\\ \end{aligned} \right.\\ x(t_0)=x_0 { x⋅=f(x,u,t)y=h(x,u,t)x(t0)=x0所以在t时刻,所有状态变量就可以用n维的向量空间描述,也即状态空间。在一个时间区间内,状态空间所有的状态量的点集就构成了一条轨迹。
-
我们梳理一遍:
-
状态
系统在时间域中的行为或运动信息的集合,表征了系统运动的信息和行为。
-
状态变量
对状态变量有两个要求,一是要求最少,二是要求完整,就是说要用系统中的一组最少的变量去表征系统。当我们知道一个系统的初始条件和系统在初始时间以后的输入的话,就能完全确定该系统在任何时间的行为。
- 状态变量的选取不是唯一的,但是选取的状态变量是独立的
- 状态变量本身是数学上的概念,并不需要在物理上有意义或能被测量。
- n 阶系统有 n 个独立的状态变量,且有 n 个独立的初始条件
-
状态向量
能够完全描述一个系统行为的 n n n 个状态变量,将它们看作向量 x ( t ) x(t) x(t) 的分量,则 x ( t ) x(t) x(t) 称为状态向量,记作 x ( t ) = [ x 1 , x 2 , ⋅ ⋅ ⋅ , x n ] T x(t)=[x_1,x_2,···,x_n]^T x(t)=[x1,x2,⋅⋅⋅,xn]T
-
状态空间与状态轨迹
状态空间是 n 个状态变量作为坐标系所组成的 n 维空间,也是状态向量 x(t) 所在的空间。
状态轨迹则是,在状态空间中状态向量端点随时间变化而描出的路径。
-
状态方程
我们将系统的状态向量与输入之间建立关系式(一组一阶微分方程),这种关系式就称为状态方程: x(t) ⋅ = f ( x , u , t ) \mathop{\textbf{x(t)}}\limits^{·}=f(\textbf{x},\textbf{u},t) x(t)⋅=f(x,u,t)
-
输出方程
我们将系统的输出与状态向量、输入之间建立关系式(一个代数方程),这种关系式就称为输出方程: y(t) = h ( x , u , t ) \textbf{y(t)}=h(\textbf{x},\textbf{u},t) y(t)=h(x,u,t)
-
状态空间表达式
我们将状态方程和输出方程放在一起,就构成了系统的状态空间表达式,又称动态方程。
公式
{ x ⋅ = f ( x , u , t ) y = h ( x , u , t ) \left\{\begin{aligned}\mathop{\textbf{x}}\limits^{·}=f(\textbf{x},\textbf{u},t) \\ \textbf{y}=h(\textbf{x},\textbf{u},t)\\\end{aligned}\right.\\ { x⋅=f(x,u,t)y=h(x,u,t) -
当用状态方程模型来表示线性系统的时候,可以更简单的表述为:
{ x ⋅ ( t ) = A ( t ) x ( t ) + B ( t ) u ( t ) y ( t ) = C ( t ) x ( t ) + D ( t ) u ( t ) \left\{\begin{aligned}\mathop{\textbf{x}}\limits^{·}(t)={\textbf{A}}(t){\textbf{x}}(t)+{\textbf{B}}(t){\textbf{u}}(t) \\ {\textbf{y}}(t)={\textbf{C}}(t){\textbf{x}}(t)+{\textbf{D}}(t){\textbf{u}}(t) \\\end{aligned}\right.\\ {
x⋅(t)=A(t)x(t)+B(t)u(t)y(t)=C(t)x(t)+D(t)u(t)
- A A A 是状态矩阵
- B B B 是输入矩阵
- C C C 是输出矩阵
- D D D 是直接转移矩阵
u u u 与 y y y 分别是输入和输出变量, A , B , C , D A,B,C,D A,B,C,D 都是维数相容的矩阵。
当四个矩阵与时间均无关,我们又可以称之为线性时不变系统:
{ x ⋅ ( t ) = Ax ( t ) + Bu ( t ) y ( t ) = Cx ( t ) + Du ( t ) \left\{\begin{aligned}\mathop{\textbf{x}}\limits^{·}(t)={\textbf{A}}{\textbf{x}}(t)+{\textbf{B}}{\textbf{u}}(t) \\ {\textbf{y}}(t)={\textbf{C}}{\textbf{x}}(t)+{\textbf{D}}{\textbf{u}}(t) \\\end{aligned}\right.\\ {
x⋅(t)=Ax(t)+Bu(t)y(t)=Cx(t)+Du(t)
2.1 使用 ss() 建立系统状态方程模型
代码如下:
A =[0, 1, 0; 0 0 1; -6 -11 -6];
B = [1 0; 2 -1; 0 2];
C = [1 -1 0; 2 1 -1];
D = zeros(2);
G = ss(A, B, C, D);
显示效果:
G =
A =
x1 x2 x3
x1 0 1 0
x2 0 0 1
x3 -6 -11 -6B =
u1 u2
x1 1 0
x2 2 -1
x3 0 2C =
x1 x2 x3
y1 1 -1 0
y2 2 1 -1D =
u1 u2
y1 0 0
y2 0 0Continuous-time state-space model.
2.2 使用 ssdata() 获取状态方程对象参数
代码如下:
[a,b,c,d] = ssdata(G);
[a,b,c,d,Ts] = ssdata(G);
或者直接使用 G.a 的命令来提取。
2.3 带有时间延迟的状态方程模型表示
可以表示为:
{ x ⋅ ( t ) = Ax ( t ) + Bu ( t − τ ) y ( t ) = Cx ( t ) + Du ( t − τ ) \left\{\begin{aligned}\mathop{\textbf{x}}\limits^{·}(t)={\textbf{A}}{\textbf{x}}(t)+{\textbf{B}}{\textbf{u}}(t-\tau) \\ {\textbf{y}}(t)={\textbf{C}}{\textbf{x}}(t)+{\textbf{D}}{\textbf{u}}(t-\tau) \\\end{aligned}\right.\\ {
x⋅(t)=Ax(t)+Bu(t−τ)y(t)=Cx(t)+Du(t−τ)
输入模型的时候使用如下代码即可:
G = ss(A, B, C, D, 'IODelay', Ts); % Ts 为上面的时间延迟tau
3 线性系统的零极点模型
系统的传递函数模型给出之后,我们可以马上知道系统的零极点模型。
3.1 使用 zpk() 表示零极点模型(零点极点)
代码如下:
G = zpk(Z, P, K); % Z 为系统的零点列向量,P 为系统的极点列向量,K 为系统的增益
例如下面的零极点模型:
G ( s ) = ( s + 1.539 ) ( s + 2.7305 + 2.8538 j ) ( s + 2.7305 − 2.8538 j ) ( s + 1 ) ( s + 2 ) ( s + 3 ) ( s + 4 ) G(s)={\frac{(s+1.539)(s+2.7305+2.8538j)(s+2.7305-2.8538j)}{(s+1)(s+2)(s+3)(s+4)}} G(s)=(s+1)(s+2)(s+3)(s+4)(s+1.539)(s+2.7305+2.8538j)(s+2.7305−2.8538j)
则我们代码如下:
P = [-1; -2; -3; -4];
Z = [-1.539; -2.7305+2.8538i; -2.7305-2.8538i];
G = zpk(Z, P, 1);
则 matlab 的输出结果为:
G =
(s+1.539) (s^2 + 5.461s + 15.6)
-----------------------------
(s+1) (s+2) (s+3) (s+4)
Continuous-time zero/pole/gain model.
当没有零点的时候,我们使用空向量来代替,比如说:
系统的开环传递函数为:
G ( s ) = 1.5 s ( s + 1 ) ( s + 2 ) G(s)={\frac{1.5}{s(s+1)(s+2)}} G(s)=s(s+1)(s+2)1.5
我们使用matlab描述则格式如下:
G = zpk([], [0, -1, -2], 1.5);
3.2 使用 pzmap() 来绘制零极点位置
代码如下:
pzmap(G);
绘制出的图像如下:
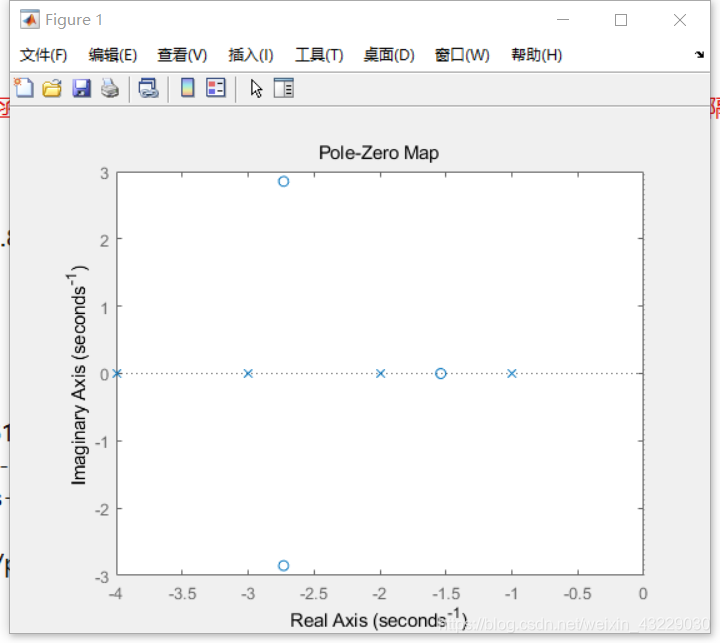
3.3 使用 tf2zp() 来求取传递函数模型系统的零极点
代码如下:
num = [4 16 12];
den = [1 12 44 48 0];
[z, p, K] = tf2zp(num, den);
Matlab 输出结果如下:
z =
-3
-1p =
0
-6.0000
-4.0000
-2.0000K =
4
零点位于 s = -3 和 -1。极点位于s =0, -6, - 4 和 -2。增益 K 是 4 。
4 多变量系统的传递函数矩阵模型
此处笔者未涉猎,暂时不写,等涉猎了继续补充
5 动态系统数学模型的相互转换
5.1 传递函数模型到状态空间模型的变换 ( tf2ss )
命令:
[A, B, C, D] = tf2ss(num, den);
将具有传递函数形式:
Y ( s ) U ( s ) = n u m d e n = C ( s I − A ) − 1 B + D {\frac{Y(s)}{U(s)}} = {\frac{num}{den}}={\textbf{C}}(s{\textbf{I}}-{\textbf{A}})^{-1}{\textbf{B}}+D U(s)Y(s)=dennum=C(sI−A)−1B+D
的系统变换为状态空间形式:
{ x ⋅ ( t ) = Ax + Bu y ( t ) = Cx + D u \left\{\begin{aligned}\mathop{\textbf{x}}\limits^{·}(t)={\textbf{A}}{\textbf{x}}+{\textbf{B}}{\textbf{u}} \\ {\textbf{y}}(t)={\textbf{C}}{\textbf{x}}+D{\textbf{u}} \\\end{aligned}\right.\\ {
x⋅(t)=Ax+Buy(t)=Cx+Du
特别注意的是,任何系统的状态空间表达式都不是唯一的。同一个系统具有许多个(实际是无限多个)状态空间表达式。 MATLAB 命令只给出这些表达式中的一种可能形式。
5.2 状态空间模型到传递函数模型的变换 ( ss2tf )
命令:
[num, den] = ss2tf(A, B, C, D, iu); % 对于输出量多于1个的系统必须指定iu,例如系统有3个输入那么iu必须是1,2或3
以下同理
5.3 状态空间模型到零点-极点模型的变换 ( ss2zp )
5.4 零点-极点模型到状态空间模型的变换 ( zp2ss )
5.5 传递函数模型到零点-极点模型的变换 ( tf2zp )
5.6 零点-极点模型到传递函数模型的变换 ( zp2tf )
5.7 连续时间系统到离散时间系统的变换 ( c2d )
命令:
[G, H] = c2d(A, B, Ts);
可以将连续时间状态空间模型变换为离散时间状态空间模型,其中 Ts 是以秒为单位表示的采样周期。这里假设输入端有个零阶保持器。也就是说,采用上述命令,能将:
x ⋅ = Ax + Bu \mathop{\textbf{x}}\limits^{·}={\textbf{A}}{\textbf{x}}+{\textbf{B}}{\textbf{u}} x⋅=Ax+Bu
变换为:
x ( k + 1 ) = Gx ( k ) + Hu ( k ) {\textbf{x}}(k+1)={\textbf{Gx}}(k)+{\textbf{Hu}}(k) x(k+1)=Gx(k)+Hu(k)