机器学习入门1:线性回归
1.线性回归概念
通过线性关系来描述输入到输出的映射关系,常见的应用场景有:网络分析、银河风险分析、基金估价预测、天气预报……
2.线性回归例子
假设有一组数据,通过画图的方式显示出来。我们发现这些数据的点大部分都落在某一条线上面,那么我们可以尝试线性回归来做模型。尝试找出最佳的参数W,可以通过特征变量X的线性关系来预测结果Y。
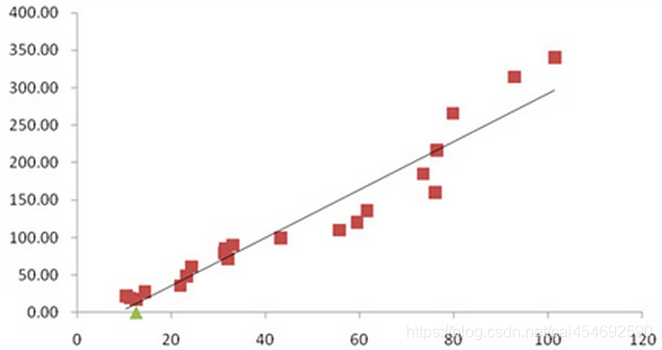

假设特征X1,X2,X3与结果Y存在某种线性关系,但是我们并不知道最佳参数a,b,c,d具体的值。(a,b,c就是上图模型的w1,w2,w3)接下来,我们看下图:
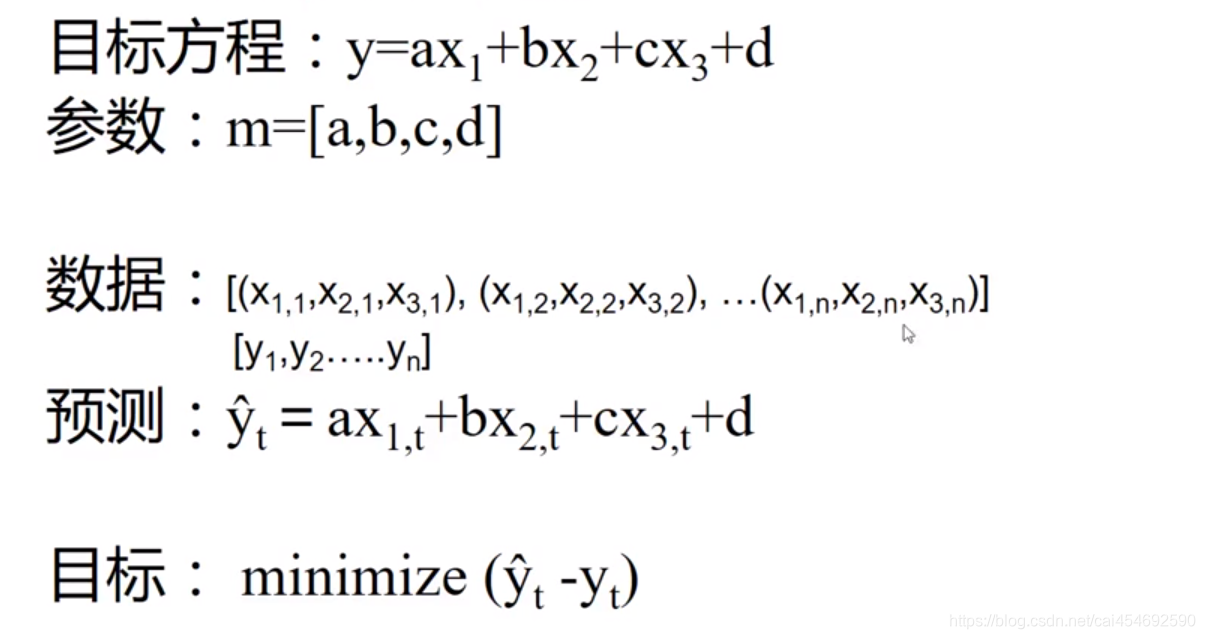
怎么样才算是最佳参数a,b,c,d呢?
最佳系数a,b,c,d应是输入变量X结合系数a,b,c,d得出的预测结果Y与真实结果Yt相近,预测结果Y与真实结果Yt相减的结果越小,证明映射关系就越好。怎么找出最小的结果?我们就要使用最优化方法去解决这个问题。
3.梯度下降 / 上升法
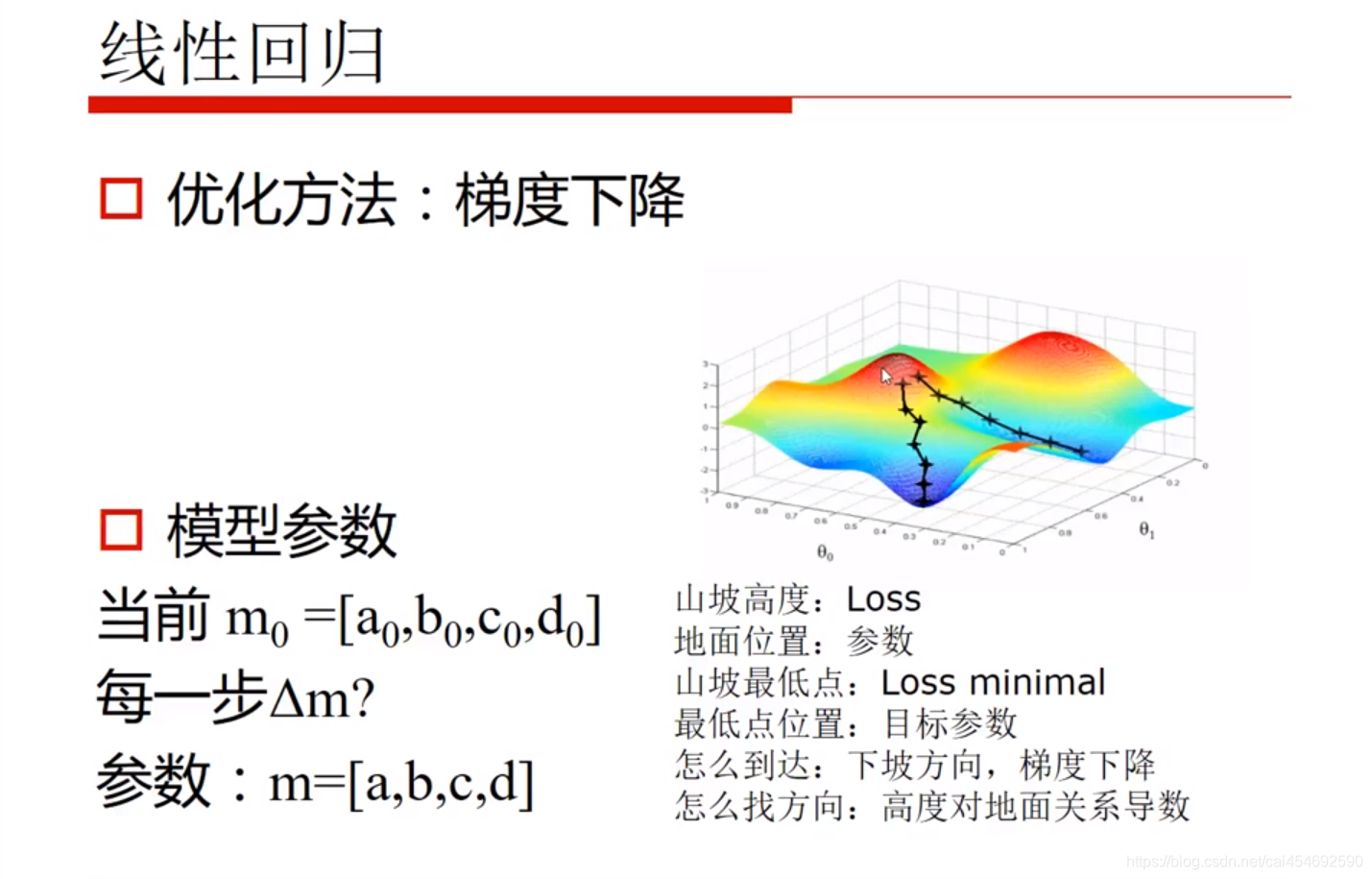
如上图:
梯度下降法相当于在一个山坡寻找一个最低点,其中:
- 山坡高度:Loss就是你的预测结果Y与实际结果Yt的差别
- 地面位置: 参数
- 山坡最低点:目标参数
- 怎么到达: 下坡方向,梯度下降
- 怎么找方向: 高度对地面关系的导数
这里,就帮大家复习一下导数的定义:
导数(Derivative),也叫导函数值。又名微商,是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f’(x0)或df(x0)/dx。
导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。
不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。
对于可导的函数f(x),x↦f’(x)也是一个函数,称作f(x)的导函数(简称导数)。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上,求导就是一个求极限的过程,导数的四则运算法则也来源于极限的四则运算法则。 反之,已知导函数也可以倒过来求原来的函数,即不定积分。微积分基本定理说明了求原函数与积分是等价的。求导和积分是一对互逆的操作,它们都是微积分学中最为基础的概念。
所以要找出最低的位置,就是朝下走某个梯度m,不停地往下走直到达最低点位置。
那么对于线性方程我们要怎么算呢?我们求的是高度(Loss)与位置(参数)的关系 那就是算Loss对参数a,b,c,d的导数就是梯度
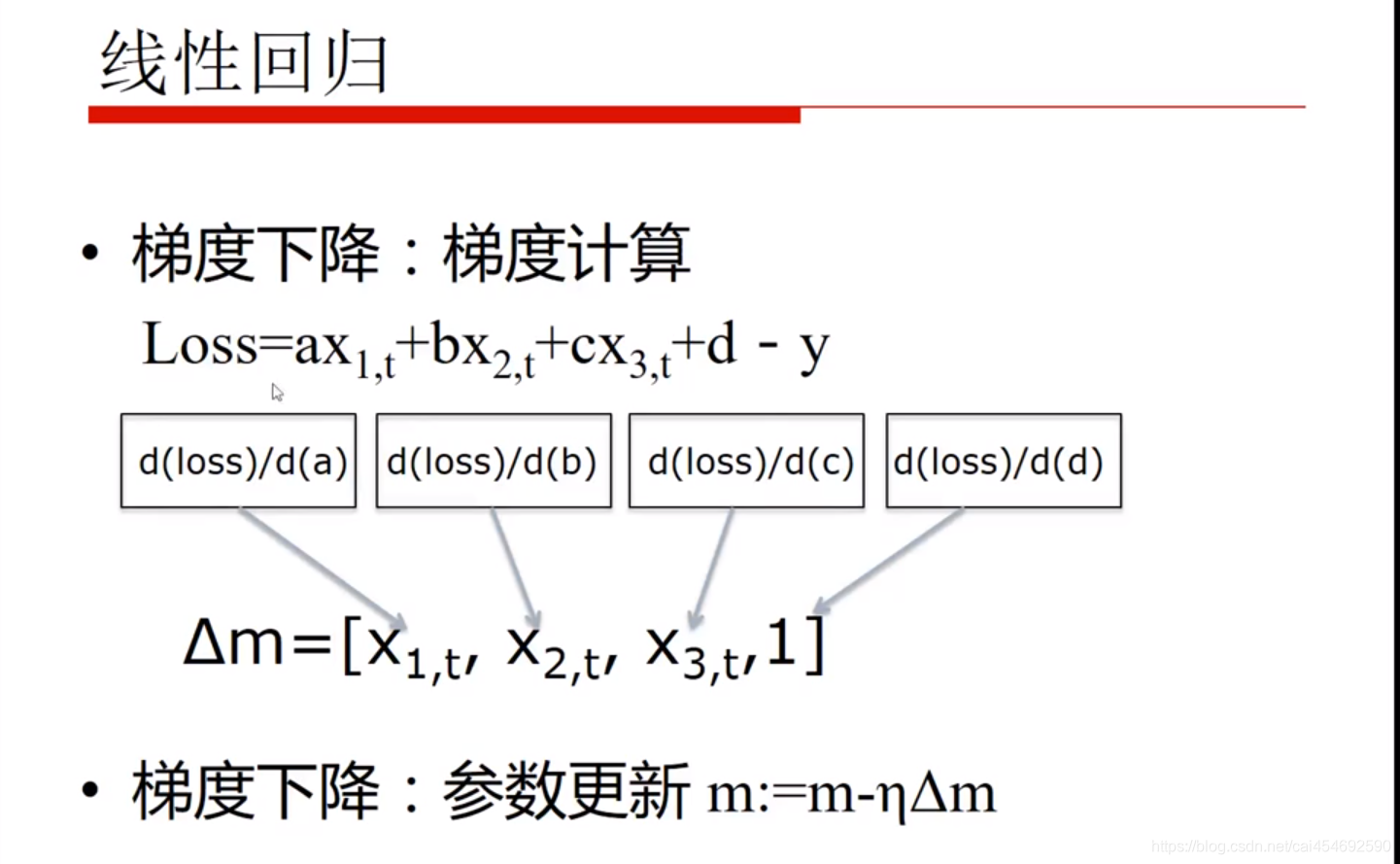
我们分别对参数a,b,c,d单独求导就可以得出特征值X1,X2,X3,得到梯度后,我们可以进行梯度更新。然后就很容易找到了最低点。。。
