导函数的形式：
推导： 
例题： 求：
,在 h-> 0 时的导数；
左极限，左导数等价； 右极限，右导数等价；
对于间断点处，必须用定义证明其导数。
例题： 求：
在x=1处的可导性。
二项展开式：
排列组合计法：
排列组合法的理解：
导函数的定义式：
y', f'(x) 或 dy/dx;
常见导函数公式：
1. (a^x)' = a^x * ln a; （logˇa x)' = 1/x* ln a ;
2.sinx ' = cosx , cosx ' = -sinx , tanx ' = sec^2 x , 注： 余割：csc x = 1/ sinx ; 正割： sec x = 1/ cos x; 余切：cot x = 1/tanx;
3.sec x ' = tanx * sec x ; csc x ' = - csc x*cot x; cot x ' = - csc^2 x ;
导数的几何意义：
法线方程： y - f(xˇ0) = - 1/f'(xˇ0) *(x-xˇ0);
切线方程： y- f(xˇ0) = f'(xˇ0)* (x-xˇ0);
可导，连续，极限三者间的关系：
函数在一点可导，则函数在该点 一定 连续；
函数在一点连续，函数在该点不一定可导。 （如： y = |x|;）
可导 -----> 连续-----> 有极限； 连续 ----\---> 可导； 无极限 ----> 不连续 ----> 不可导；
函数的求导法则：
*四则运算：
1.（x +- y +- z )' = x' +- y' +- z'
2. (x*y*z)' = x'yz + xy'z + xyz'
3.(x/y)' = ( x'y -xy' ) / y
*反函数的求导法则：
1.关于 y=x 对称 的两直线 斜率关系： kˇ2 = 1/kˇ1; ，即 f'(x) = 1/f'(y) ;
例子： y = arc sin x; y = arc tan x; （注意，函数的复合关系运算式： sin( arc sin x )） = x );
常见的三角函数的反函数求导结果：
1.弦类： 
2.切类： 
3.割类：待定...
*复合函数求导法则：
, 链式法则；
关键点： 1.弄清复合层次；
2.从外向内相乘；
3.不漏掉任何一层；
*抽象函数求导法则：
1.注意： [f(sinx)] ' =/= f'(sinx), 它们选定的参数不同， 前者是以 x, 而后者 的sinx 相当于 x。变为了一个形参。
2.注意： 抽象函数的求导，可近似看成简单函数求导。
*高阶倒数的求导法则：
高阶导的物理意义： 一阶导： 速度； 二阶导： 加速度；
常见函数的高阶导公式：
1.多项式的高阶导： y= a0 * x^n + a1* x^(n-1) +....+ an* x^0 ;
若n在定义的 项 数 区间内： 
若n 不在 定义的 项数 区间内： 
2.指数的高阶导： 
3.正弦函数的高阶导：
4.复合函数的高阶导（2阶）： y = f( ln x)
，注意 ： 对 复合一阶导 求 导的情况:(y')' = [ f'(ln x) ]' = f''(lnx)*1/x， 之所以会这样，是因为求导的时候，参照的是因变量，此时的因变量为： x。
5.乘积的高阶导：
隐函数：
定义：由二元方程确定的式子。
属性：
任意一个显函数都可以转化为隐函数；
隐函数 不一定 都能 转化为 显函数；
*隐函数的求导法则：
将式子中的 y 看成 y(x)求导，即 y' = y' ； eg: ( ln y )' = y'/y; （理解： 显示函数中，有： x' = 1）。
1.取对数法； 2： 取指数法； （说明，主要是针对 幂 指 函数）；
*由参数方程确定的曲线求导法则：
由链式法则，和 反函数求导法则，可推导出：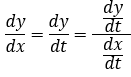 
二阶的情况（全局都是以 t 作为因变量）： 
三阶的情况（全局都是以 t 作为因变量）： 
微分：
定义： y = f(x), ∆y = f(x + ∆x) - f(x), 可表示成： ∆y = A ∆x + O(∆x).其中A 为 不依赖于 ∆x 的常数。
此时，称： 函数 y = f(x) 在 点x 可微。
而 A∆x 叫做 y = f(x) 的微分，记住： dy；
可微与 可导的关系：
可微 《===》 可导， 且： dy = f'(x) * ∆x ；
dy = f'(x)dx , f'(x) = dy/dx，导数实质就是微分之商。
微分的几何意义：
切线的纵坐标增量的变动情况；
当 ∆x --> 0时，∆x ~= dy, 则 f(x) ~= f(x0) + f'(x0)(x-x0)。 它的意义是，将曲线上的点代入直线研究其性质。
微分的运算法则：
1.四则运算同导数；
2.复合函数的不变性:
dy = df[g(x)] = f'[g(x)]*dg(x) = f'[g(x)]*g'(x)*d(x)， 可见，它是从 外层 至 内层依次求微分，直至求到 dx。
3.隐函数运算法则：
复合函数的中间不变性。 即 x 与 y 的地位平等，不需将 y 看成 x 的函数；
4.凑微分法则：
待定；
5.函数值的近似运算公式： f(x) ~= f(x0) + f'(x0)(x - x0);
eg: f(x) ~= f(0) + f'(0)x; 注意，这里的函数值，是任意值。
微分中值定理：
1.费马定理： 若f(x) 在x=x0处可导，且为极值点， 则其导数： f'(x0) = 0;
2.罗尔定理：
y = f(x) 在 [a,b]连续，在(a,b)可导，称： f(x)在[a,b]平滑；
当f(a) = f(b) 即函数等高时，则
在(a,b)内，至少存在一点： ξ，使得 f ' (ξ) = 0;
驻点： 可导函数的每两个零点之间，存在的一个导数为零的点；
拐点：一阶导数的每两个零点之间 ，存在的一个二阶导数为零的点；
零点定理的前提： 函数必须连续；
使用场景:
1.题目中出现： f'( ξ)时候，可考虑。
2.证明方程的零点存在。（方法有： 零点定理； 罗尔定理，其关键是找 辅助函数；）
拉格朗日中值定理：
定义： 若 y = f(x) 满足：(1)在[a,b]上连续； (2):在(a,b)内可导；
则至少存在一点 ξ ∈(a,b),使 f(b) - f(a) = f'(ξ)(b -a ),即
[ f(b) - f(a) ] /( b - a ) = f'(ξ): 其解释为：存在一点ξ，使得 a,b 两点割线斜率 = 点ξ 的 切线斜率；
有限增量公式： ∆y = f ' (x + θ*∆x) * ∆x ,(0<θ<1) ， ( 函数值的近似计算公式：∆y ~= f'(x0) * ∆x)
定理：
在一个区间上导数恒等的两个函数只相差一个常数；
应用例题：
（1）不等式证明：|f'(x)| ≤ M => |f(x) - f(y)| ≤ M|x-y|
（2）证明恒等式 为常值函数；
柯西中值定理：
定义： 设函数 f(x) 和 F(x)在 [a,b]连续，在(a,b)可导,则有：[ F(b) - F(a)] *f ' (ξ) = [f(b) - f(a) ]* F ' (ξ)。
且F '(x) ≠0时，存在 ξ∈(a,b),St 