基本初等函数--->初等函数： 有限次四则运算；
极限存在法则一：夹逼准则：
eg:对于无穷项四则运算，lim 1/(n^2+1) + 2/(n^2+2) + ....+ n/(n^2+n)
极限存在法则二：单调有界定理：
eg:知道首项和关系项 的 递归数列。
x1 =10, x n+1= 
其解决步骤：
1.求单调性（根式有理化）， 关键： 
与 
同号，即与 
同号。
2.证有界；
3.对关系式求极限；
关于无穷小量的重要极限1：
推论：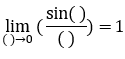 
常见的几个实现：
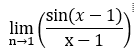
关于无穷小量的重要极限2（幂指函数的无穷大量）：
<----> 
推论：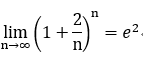 
无穷小量的比较：
1.高阶无穷小：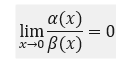
，称为： 阿尔法 是 碑拓 的高阶无穷小，反之。 记作： 阿尔法= O(碑拓)
2.低阶无穷小：同上类比。
3.同阶无穷小：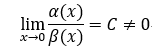
,C为常数。 称为: 阿尔法 是 碑拓 的 同阶无穷小。
4.K阶无穷小：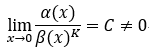 
,C为常数，称为: 阿尔法 是 碑拓 的 K阶无穷小。
5.等价无穷小：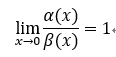 
,称为： 阿尔法 是 碑拓 的等价无穷小。 记作： 阿尔法 ~ 碑拓。
无穷小量的运算：
低阶无穷小 + 高阶无穷小 = 低阶无穷小。 即： 
等价无穷小的性质：
1.自反性； 2.对称性； 3.传递性；
等价无穷小定理一：
若，α ~ β，则 α - β =O(α) 或 O(β)
等价无穷小定理二：
若，α ~ β，则 lim f(x)*α = lim f(x)*β
推论： α ~ α1, β~ β1 ,则 lim f(x)*α / lim f(x)*β = lim f(x)*α1 / lim f(x)*β1 。
常用的等价无穷小：
1.sinx ~ x;
2. arc sinx ~ x;
3.tan x ~ x;
4.arc tan x ~ x;
5. 1- cosx ~ x^2/2;
6.ln(1+x) ~ x;
7.e^x -1 ~ x;
8.(1+x)^(1/n) -1 ~ x/n;
9.(1+x)^(1/2) -1 ~ x/2;
函数连续的定义：
定义一： 
： 前提： 1.x0 处函数有定义； 2.x0 处 有极限； 3.极限与函数值相等。
定义二： ∀ε>0,∃δ>0,当 |x - x0| <δ时，有:|f(x) - f(x0)|<ε。
函数的左连续：
函数的右连续：
分段函数的连续性： 除了要考虑分段点外，还要考虑分段点处的连续性。
函数的第一类间断点：
1.极限存在（无定义，或 有定义但函数值与极限不相同），称为 ：可去间断点；
2.极限不存在，但左右极限存在，称为：跳跃间断点。（注意，此时，左右极限必须不相同。）
函数的第二类间断点：
1.至少有一侧 是 以 无穷为 极限 的点，称为： 无穷间断点。
2.不断震荡的极限情况； 称为震荡间断点。
如： 函数 
其在点x=0处没有定义，且当x趋于0时，函数值在-1,1这两个数之间交替振荡取值，极限不存在。
函数的连续性质：
1.连续函数的四则运算：若 f(x)，g(x)在 x0连续，则，f(x)+-g(x), f(x)*g(x) , f(x)/g(x) 连续。
推论：两个连续函数的 和，差，积，商（分母不为零）仍然连续。 如： tanx = sinx/cosx
2.反函数的连续性：
若f(x)在定义域内单调且连续，则x=f ^(-1)(y) 在定义域内单调且连续。
3.复合函数的连续性： 设 u = g(x)
1.若 lim g(x) = u0,(x->0); limf(u) =f(u0),(u->u0); 则 lim f[g(x)] = f(u0),(x->0);
说明： 复合函数，内极限，外连续，则极限运算与 连续函数运算顺序可交换。
2.若u=g(x) 在 x0处连续，且 y= f(u) 在 u0 = g(x0)连续，则y = f[g(x)] 在x0处连续；
说明： 复合函数，内连续，外连续，则总体任然是连续函数。
4.基本初等函数：
基本初等函数在定义域内连续。
5.一切初等函数，在其定义区间上连续。
可利用该性质求极限：
1.若为连续函数，代入函数即可。
2.外函数连续，则对内函数求极限，再代入。
6.幂指函数的连续性： (g(x))^(f(x))
1.确定型：
x-x0时，f(x) ->b , g(x) -> a,则： lim( (g(x))^(g(x)) )= a^b；
2.未定型：
1. 1^ ∞ 类型，如： lim(1+2x)^(3/sinx),x->0；
2.∞^0类型。
3.0^0类型。
它们的处理方法： 变换为： lim e^ ( f(x)*ln g(x) )处理。 主要的思路是，将幂指函数化简为基本函数，原因是：利用指数，将一个指数转换为对数，然后对数 与 幂数 狼狈为奸。。
例题： lim (cosx) ^(1/ln(1+ x^2)), x-> x0;
最值定理：
f(x)在[a,b]上连续，则函数有界，取到最值。
零点定理：
f(x) 在 [a,b]上连续，且 f(a) 与 f(b) 异号，则 至少 存在一点 ξ，使得 f(ξ) = 0;
介值定理：
f(x) 在 [a,b]上连续，且M 和 m 分别是 f(x) 在[a,b]上的最值，则对任意的C 介于 [m,M]之间，在(a,b)至少存在一点 ξ，
使得， f(ξ) = C。
举例： f(x) 在[0,1]连续，对[0,1] 任一点x 有， 0<= f(x) <= 1,证 [0,1] 中必然存在一点c,使得 f(c) = C;