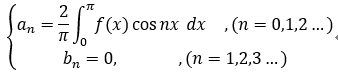常数项级数：
概念： 用圆内接正多边形面积逼近圆面积，依次作圆内接正 3*2^n (n=0,1,2 ... L)边形，设 a0 表内接正三角形面积，ak 表增加的面积， A = a0+ a1+L + an+ L;
定义： 给定一个数列，u1,u2,L , un, 其为 常数项无穷级数(一般项，或者通项): u1 + u2 + L + un + L 的部分
部分和：
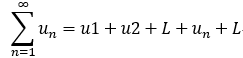
称为
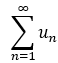的部分和；
敛散性：
若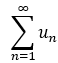的部分和数列 {sn} 有极限s, 则 
称 无穷级数收敛；
等比级数（几何级数）：
敛散性: |q| <1 时，等比极数收敛；
|q| >=1 时， 等比级数发散； 其中，q指的是 等比公项；
性质1: 若等比级数收敛，则其k倍仍然收敛；
性质2：若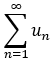
与 
均收敛，则 
也收敛，且 和为： s1+s2;
另： 收敛级数 + 发散级数 = 发散级数； 发散级数+ 发散级数 不一定= 发散级数；
如： Un = (-1)^(2n) Vn = (-1)^(2n+1);
性质3： 在级数中去掉 有限项，不影响敛散性；
性质4： 若加括号后的级数发散，则原级数必发散；（发散级数 去 括号后 所形成的 级数 必发散）
注意： 收敛级数 去 括号后 所形成的 级数不一定收敛；
若级数收敛，则对级数的项任意加括号后仍收敛；
收敛级数的必要条件：
1.若级数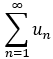 
收敛，则 必有： 
其逆否命题： 
==> 级数发散； （判断级数发散的方法）
eg: 证明调和级数: 
是发散的。（反证法）
若收敛，有 
, 
,
矛盾。
2. 若级数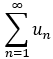收敛，则 
发散；
常数项级数审敛法：
定义法： 部分和极限存在；
1.正项级数 Un >=0 <==> 部分和数列Sn 有界；（不常用）
2.比较审敛法：
设 
,
是两个正项级数，对 ∀n ∈ N, 有： Un (弱) <= Vn (强),
则： 1.若级数 收敛，则也收敛；
2.若级数发散，则也发散；
3.P级数：
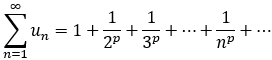
当 0<p<= 1时，p级数发散；
当 p>1时， p级数收敛；
4.比较审敛法的极限形式：
当 0<L <∞ 时，两个级数 同时收敛 或者 同时发散；
当 L =0 且 
收敛时，
也收敛；
当 L = ∞ 时，且发散时，也发散；
eg: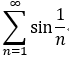 
发散； 注： 
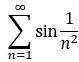收敛
正项级数审敛法的乘法形式：
取 
则：
，其中L 为 非零常数。
此时，若 0<p<=1, 则 发散。 (极限审敛法)；
若 p>1 或者 p = ∞时， 级数收敛。
比值审敛法（达朗贝尔判别法）：
若 为正项级数，且 
则： 若 0<= ρ<1时，级数收敛；
若 ρ>1 或者 ρ=∞时，级数发散；
注意，这里刚好与p级数的情况相反；
若 ρ=1时，不能适用；
交错级数审敛法（符号一正一负交替出现）：
1.莱布尼兹定理：
若交错级数满足条件：
1.若 U n >= U n+1 ,(数值分布而言)；
2.
则级数：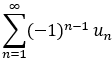
收敛，且 其和 S <= u1 , 余项和 Rn <= U n+1
若交错级数收敛，其绝对值后仍然收敛，称为 绝对收敛， 如：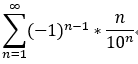 
若交错级数收敛，其绝对值后发散，称为 条件收敛，如：
， 
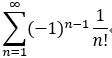
2.绝对收敛的级数一定收敛.(判断交错级数的敛散性 或者 一般级数)；
eg:
幂级数：
函数项级数的概念：
为定义在 区间 I 上的函数项级数；
对 x0 ∈ I, 若它 收敛，则称 ： x0 为 收敛点，所有的收敛点全体称为 收敛域；
若它 发散，则称： x0为发散点， 所有的发散点全体称为发散域；
eg: 
当： |x| <1时，收敛， 此时 S(x) = 
,称为 和函数；
|x| >1时，发散.
幂级数的标准形式：
，取 x0 = 0, 则有：
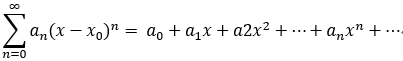
幂级数收敛域特点：
关于原点对称；
阿贝尔定理：
若幂级数在 x= x0 (x0=/=0) 处收敛，则此幂级数在满足不等式 |x|<= |x0|的一切x处绝对收敛。 (x0 称为收敛半径，记作R)
反之，若幂级数在x = x0 处发散，则对于 |x| > |x0| 处的x发散；
当R = 0时，幂级数仅在x = 0 处收敛；
当R = +∞时，幂级数在 （-∞，+∞）收敛；
当R =/=0 和 +∞ 时，
当|x| < R 时，幂级数绝对收敛；
当|x| > R 时， 幂级数发散；
当|x| = R 时，可能收敛，也可能发散，需要单独讨论；
若幂级数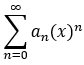 
的系数满足： 
则 当 ρ=/= 0 时， R = 1/ ρ;
当 ρ=0 时， R = +∞；
当 ρ= +∞时，R = 0；
即： 收敛半径 R = 
幂级数的运算：
运算后的收敛域 = min{r1,r2};
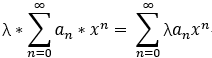
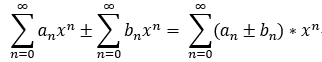
连续性： 和函数在 收敛域内 连续；
可积性： 和函数在收敛区间可积分，并且可逐项积分；
即：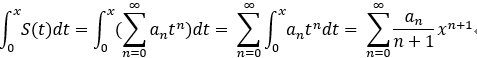 
可导性： 和杉树在收敛区间可导 ，且可 逐步求导；
即：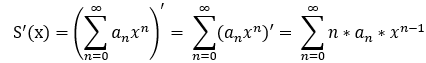 
eg: 求幂级数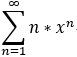 
的和函数 S(x);
注意: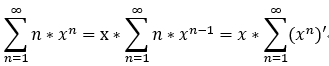 
另：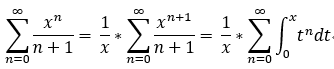 
泰勒级数：
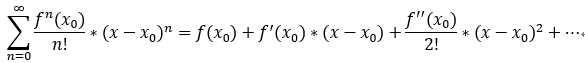
当 x0 =0 时，称为： 麦克劳林级数；
展开成泰勒级数的充要条件： 通项的极限 为 0；
展开的方法包括：
1.直接展开法，利用泰勒公式；
2.间接展开法, 利用已知函数 形式转化；
eg: 将 1/(1+x^2) 展开成幂级数：
提示: 
--> 
--> 
--> 
eg: 将 f(x) = ln(1+x) 展开成 幂级数：
解析： 
理解：它们的关键在于： 处理好 形参，与实参，以及处理过程，复合函数，的区别与联系；
傅里叶级数：
S(n) =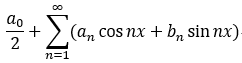 
定理一：
组成三角级数的 函数系： cosx , sinx , cos2x,sin2x,... ,cosnx sinnx,L 在 [-π，π] 上 积分等于0
则 相同的函数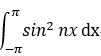
=2π ， 
=π ;
定理二：
设 f(x) 是 周期为 2π 的周期函数，且 f(x) =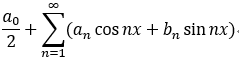 
,
则有 傅里叶系数：
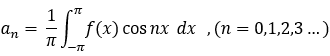
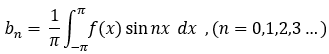
将傅里叶系数 代入 形式傅里叶级数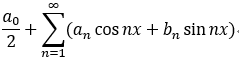： ， 则为傅里叶级数；
定理三(迪利克雷充分条件):
设 f(x) 是周期为 2π 的周期函数，若满足：
1.在一个周期内连续，或只有有限个第一类间断点
2.在一个周期内至多有有限个极值点
则 f(x) 的傅里叶级数收敛，其收敛点为：
定理四：
正弦级数 与 余弦级数：
若f(x) 为 奇函数， 则 f(x)cosnx 是 奇函数， f(x)sin nx 是 偶函数；
故有： 正弦级数：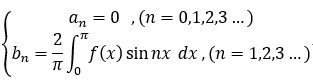 
若 f(x)为 偶函数， 则 f(x)cos nx 为偶， f(x)sin nx 为 奇，
故有：余弦级数： 