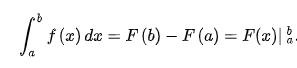高等数学超入门学习笔记

极限

百度百科

1.数列极限

百度百科

1.1 数列

1.2 数列极限

1.3 单调收敛原理

{ x n } \{x_n\} { xn​}单调递增且 { x n } \{x_n\} { xn​}有上界（可以找到实数M使 { x n } \{x_n\} { xn​}中任意一项小于M）， { x n } \{x_n\} { xn​}收敛（存在象限a）（单调递减同理）

2.函数极限

百度百科

2.1 定义

（a的去心邻域：$(a-\delta ,a)\cup (a,a+\delta )$）
（a的左邻域：$(a-\delta ,a)$）
（a的右邻域：$(a,a+\delta )$）

2.2 函数的单侧极限

设函数$f(x)$在点$x_0$的左邻域内有定义，如果存在常数A，对于任意给定的正数$ϵ$，总存在正数$\delta$，使得当$x$从左侧趋于$x_0$时，也即$x$满足的不等式为$0<x_0-x<\delta$时，函数值$f(x)$都满足不等式

$|f(x)-A|<ϵ$,

则常数A就叫做函数$f(x)$在$x_0$处的左极限，记作

$\underset{x\to x_0^{-}}{\lim }f(x)=A$

同样地，设函数$f(x)$在点$x_0$的右邻域内有定义，如果存在常数A，对于任意给定的正数$ϵ$，总存在正数$\delta$，使得当$x$从右侧趋于$x_0$时，也即$x$满足的不等式为$0<x-x_0<\delta$时，函数值$f(x)$都满足不等式

$|f(x)-A|<ϵ$,

则常数A就叫做函数$f(x)$在$x_0$处的右极限，记作

$\underset{x\to x_0^{+}}{\lim }f(x)=A$

2.3 函数在无穷远处的极限

设函数$f(x)$在$(t,+\infty )$内有定义，如果存在常数A，对于任意给定的正数$ϵ$，总存在正数$M$，使得当$x$满足不等式$x>M$时，函数值$f(x)$都满足不等式

$|f(x)-A|<ϵ$,

则常数A就叫做函数$f(x)$在$x\to +\infty$时的极限，记作

$\underset{x\to +\infty }{\lim }f(x)=A$

类似的，可以定义函数在负无穷远处的极限

2.4 两个基本极限

$\underset{x\to 0}{\lim }\frac{sinx}{x}=1$
$\underset{n\to +\infty }{\lim }(1+\frac{1}{n}{)}^n=e$

2.5 运算法则

2.6 连续函数

导数

百度百科

1.定义

2.几何意义

3.导函数

4.常见导数公式

$(C{)}^{\prime }=0(C为常数)$
$(x^a{)}^{\prime }=a{x}^{a-1}(a为任意实数)$
$(sinx{)}^{\prime }=cosx,(cosx{)}^{\prime }=-sinx$
$(a^x{)}^{\prime }=a^{x}lna,(e^x{)}^{\prime }=e^x$
$(lo{g}_{a}x{)}^{\prime }=\frac{1}{xlna},(lnx{)}^{\prime }=\frac{1}{x}$
$(tanx{)}^{\prime }=\frac{1}{co{s}^{2}x},(cotx{)}^{\prime }=-\frac{1}{si{n}^{2}x},(ln|x|{)}^{\prime }=\frac{1}{x}$
$(arcsinx{)}^{\prime }=\frac{1}{\sqrt{1-x^2}},(arccosx{)}^{\prime }=-\frac{1}{\sqrt{1-x^2}},(arctanx{)}^{\prime }=\frac{1}{1+x^2}$

5.求导法则

5.1 导数的四则运算法则

• $[(f(x)\pm g(x){]}^{\prime }=f^{\prime }(x)\pm g^{\prime }(x)$

• $[f(x)\cdot g(x){]}^{\prime }=f^{\prime }(x)g(x)+f(x)g^{\prime }(x)$
  推论：
  若函数$f_1(x),f_2(x),...,f_n(x)$都可导，其中$n\ge 2,n\in N$，那么$(f_1{f}_2...f_n{)}^{\prime }=f_1^{\prime }{f}_2...f_{n-1}{f}_n+f_1{f}_2^{\prime }...f_{n-1}{f}_n+...+f_1{f}_2...f_{n-1}{f}_n^{\prime }$

• $[\frac{f(x)}{g(x)}{]}^{\prime }=\frac{f^{\prime }(x)g(x)-f(x)g^{\prime }(x)}{g^2(x)}$
  推论：
  若函数$f(x)$可导，且$f(x)\ne 0$，则$[\frac{1}{f(x)}{]}^{\prime }=-\frac{f^{\prime }(x)}{f^2(x)}$

5.2 复合函数求导法则

若函数$u=g(x)$与函数$y=f(u)$均可导，则复合函数$y=f[g(x)]$可导，且$[f(g(x)){]}^{\prime }=f^{\prime }(g(x))\cdot g^{\prime }(x)$，或记成$\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx}$

定积分

百度百科

1.定积分的几何意义

1.1 黎曼和

1.2 曲边梯形的面积

设 λ = m a x { △ x 1 , △ x 2 , … , △ x n } λ=max\{△x_1, △x_2, …, △x_n\} λ=max{ △x1​,△x2​,…,△xn​}，如果当$\lambda \to 0$时，黎曼和的极限存在，那么就定义这个极限为曲边梯形的面积

1.3 定积分定义

2.定积分的计算

2.1 牛顿-莱布尼茨公式（微积分基本定理）

设$f\in C[a,b]$，如果$F(x)$是$f(x)$在区间$[a,b]$上的一个原函数，即$F^{\prime }(x)=f(x)$，那么

2.2 定积分的运算性质